Элементарные преобразования координат

Случаи или преобразования координат называются элементарными, если:

1 ) для полного совмещения осей координат необходим только поворот вокруг одной из осей; в этом случае начала систем координат совпадают, а ось поворота является общей для обеих систем (рис. 23)

Для случая элементарного поворота связь между координатами точки в системах координат 1 и 2 определяется формулой , где - координаты точки в системе ; - координаты той же точки в системе координат ; - матрица поворота. При этом положительным направлением отсчета угла следует считать отсчет по часовой стрелке при условном перемещении оси с индексом i+1 к одноименной оси с индексом I (от оси x₂ к оси x₁).

2 ) для полного совпадения осей необходимо выполнить перенос начала системы 2 вдоль одной из осей координат; в этом случае оси системы 1 и 2 параллельны и одна из пар одноименных осей систем направлена в одну сторону по одной общей прямой (рис. 24)

Для случая поворота относительно оси x матрица имеет вид:

,

где - угол поворота относительно оси x.

Для поворота относительно оси y матрица имеет вид:

где - угол поворота относительно оси y.

Относительно оси z:

Обычно в механике положительным считается поворот, происходящий против часовой стрелки, если смотреть с острия оси, вокруг которой он происходит. При преобразовании координат путем условного поворота осей до их совмещения положительный угол отсчитывается по часовой стрелке.

Преобразование координат для случая элементарного переноса производится по формуле:

,

где L – вектор, имеющий общий вид соответственно смещению систем осей 1 и 2 относительно осей x, y, z.

Совмещение двух координатных систем, произвольно расположенных в пространстве

Такое совмещение может быть осущестленно шестью элементарными поворотами и переносами, выполненными строго в следующей последовательности (повороты некоммутативны!)

1. поворот осей системы вокруг оси до тех пор, пока ось не окажется в плоскости, параллельной плоскости осей ;

2. поворот системы вокруг оси до тех пор, пока оси и 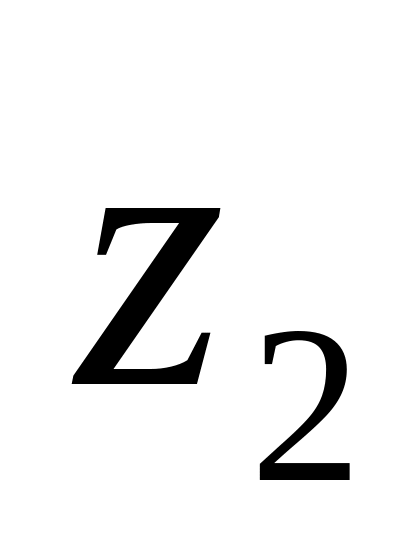не станут параллельными и одинаково направленными.

3. Поворот осей системы вокруг оси 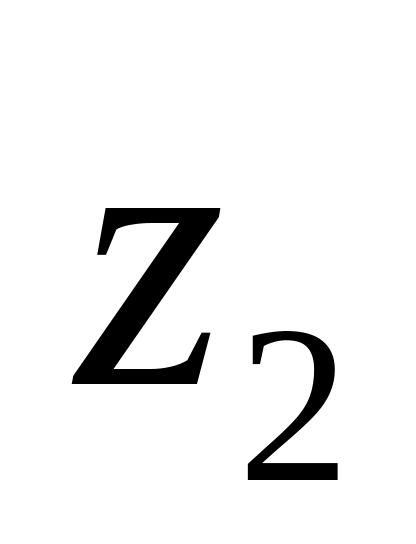до положения, при котором все оси систем 1 и 2 станут параллельны и одинаково направлены.

4. Последовательный перенос системы 2 вдоль осей , выполняемый в любой последовательности до полного совмещения осей координат.

Пример кинематического анализа манипулятора «Маскот-1»

Рассматриваемый манипулятор (рис. 25) имеет 6 степеней свободы и состоит из 6 подвижных звеньев, соединенных кинематическими парами V класса. С каждым звеном механизма связываем свою систему координат. Со стойкой - , поместив ее начало в точке 0. Со звеном 1 – систему координат , ось параллельна ; со звеном 2 - , поместив начало в точке C; ось направлена по оси звена 2, а ось - по оси вращательной пары C и т.д.

П усть координатами произвольной точки А в системе координат будут (в дальнейшем их обозначим ). Координаты этой же точки в системе

где , - матрицы-столбцы координат точки А в системах координат и ;

- матрица поворота при переходе от системы к системе ;

- матрица параллельного переноса при переходе от системы к системе .

Система может быть совмещена с системой поворотом вокруг оси на угол . Поэтому

Системе координат может быть совмещена с системой поворотом оси на угол . Матрица поворота при переходе от к имеет вид:

а матричное уравнение перехода к системе -

где - матрица-столбец координат точки А в системе .

Система координат может быть совмещена с переносом оси на величину и поворотом вокруг оси на угол . Матрица поворота при переходе от системы к системе имеет вид:

;

Матрица переноса –

Матричное уравнение перехода к системе -

где - матрица-столбец координат точки А в .

Система может быть совмещена с поворотом вокруг оси на угол . Матрица поворота при переходе от к имеет вид:

.

Матричное уравнение перехода к системе -

где - матрица-столбец координат точки А в системе .

Система может быть совмещена с переносом по оси на и поворотом вокруг на угол . Матрица поворота при переходе от системы к системе записывается в форме:

Матрица переноса –

,

Матричное уравнение перехода к системе -

где - матрица-столбец координат О в системе .

Система может быть совмещена с системой поворотом вокруг оси на угол . Матрица поворота при переходе от к имеет вид:

,

Матричное уравнение перехода к системе -

где - координаты точки А в системе .

Подставляя в последнее уравнение соответствующие матрицы M и L, получим выражения, связывающие координаты произвольной точки звена 6 в системах координат и . Введем обозначения обобщенных координат:

Тогда

где

При этом - координаты точки А в системе - координаты А в системе ; - координаты точки А в системе . Для получения скоростей и ускорений можно дифференцировать матричное уравнение. Только зная , можно определить положение точки А, заданной в системе , по отношению к системе .Скорости и ускорения точек схвата будут зависеть от скорости и ускорений обобщенных координат.