Задачи кинематического расчёта

Кинематика рассматривает закономерности движения материальных тел без учёта причин, вызвавших это движение, то есть сил и моментов. Характеристиками движения будем считать текущее положение, скорость и ускорение тел, составляющих механическую систему. Характерными для манипуляционных систем являются следующие две задачи кинематики:

прямая задача, решение которой позволяет определить положение, ориентацию, линейную и угловую скорости и ускорения звеньев механизма и их точек в инерциальной (условно неподвижной) системе координат по известным характеристикам относительного движения;

обратная задача состоит в определении характеристик относительного движения звеньев по заданным абсолютным координатам, ориентации, скорости и ускорению звеньев, отдельного звена или точек механизма.

При решении инерциальную систему координат считают декартовой, а относительное движение характеризуют обобщенными координатами, скоростями и ускорениями.

Условия выбора систем координат

При решении кинематических задач используют декартовые правые системы координат. Систему координат, связанную с неподвижным звеном механизма, называют условно неподвижной, абсолютной или инерциальной системой координат и обозначают . Для этой системы должно выполняться условие инерциальности, то есть она должна перемещаться равномерно прямолинейно или покоиться. Если это условие не выполняется ни для одного из звеньев механизма, то необходимо ввести ряд искусственных звеньев, соединяющих кинематической цепью стойку механизма (основание) с неподвижным в инерциальной системе координат звеном и обеспечивающих основанию реально существующее число степеней свободы относительно инерциальной системы координат. Все кинематические характеристики движения (координаты, скорости, ускорения) механизма в инерциальной системе координат называют абсолютными.

Преобразование прямоугольных координат

Переход от одной прямоугольной системы координат к другой прямоугольной системе координат можно осуществлять при помощи параллельного переноса (до совмещения начал координат) и поворота системы относительно начала (до совмещения осей). Поворот прямоугольной системы координат можно задать с помощью направляющих косинусов, углов Эйлера, вектора конечного поворота и т.п.

Параллельный перенос системы координат

Новые координаты связаны со старыми соотношениями (рис. 21):

о пустив индекс М

или

где - координаты нового начала координат O₁ в системе

- координаты точки в системе

- координаты точки в .

Определение углового положения систем координат с помощью направляющих косинусов

Направляющими косинусами осей системы относительно осей системы координат называются косинусы углов между соответствующими осями систем.

Например (рис.22):

Матрица направляющих косинусов

однозначно определяет условное положение системы координат относительно системы координат . Координаты точки с известными их значениями в прямоугольной системе при переходе к системе преобразуются с помощью матрицы L

В координатной форме эти преобразования записываются в виде:

Орты системы и орты связаны соотношениями:

или

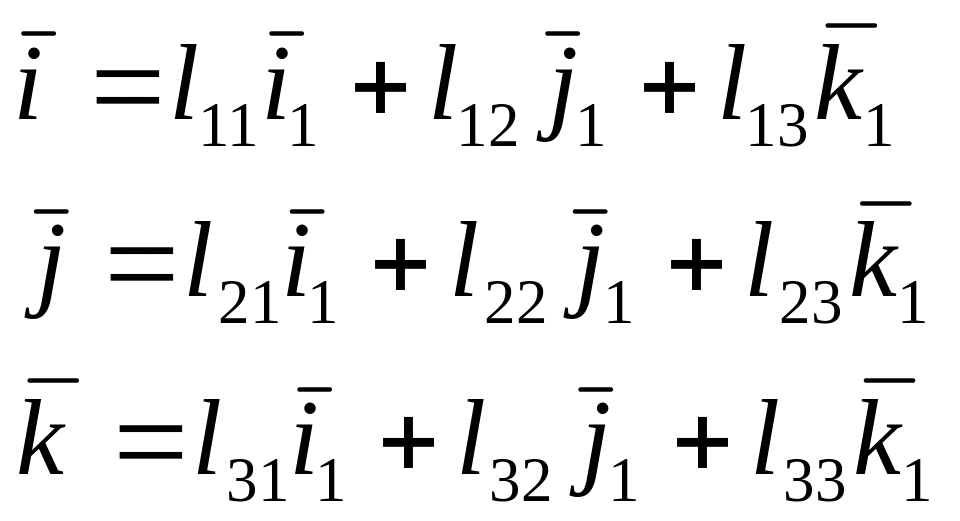
Соотношения между углами двух систем координат

Система координатных осей	Конусы углов между осями
	x1	y1	z1
x
y
z

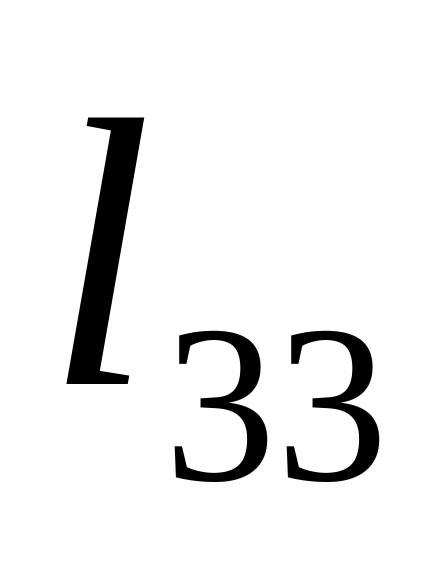
Свойства определителя преобразования

В силу ортогональности преобразования на направляющие косинусы накладывается 6 условий:

Определитель преобразования (плюс, если левая система перешла в левую или правая в правую; минус, если левая перешла в правую и наоборот)

Определение углового положения системы координат с помощью направляющих косинусов в случае конечного поворота относительно заданной оси

Пусть задана неподвижная система координат и через точку 0 проходит ось вращения n твердого тела, с которым связана система координат , а угол поворота тела относительно оси вращения равен .

а) ось вращения n задана направляющими косинусами относительно неподвижной системы координат (рис. 22). Тогда матрица направляющих косинусов для имеет вид:

Или ,

где

- транспонированная матрица

- обратная матрица.

б) ось вращения n задана направляющими косинусами в системе координат . В этом случае ,

где