Кинематический анализ манипуляторов методом преобразования координат Некоторые сведения о системах координат

Д екартовыми прямоугольными координатами точки Р называются взятые с определённым знаком расстояния этой точки до трёх взаимно перпендикулярных плоскостей или, что то же самое, проекции радиус-вектора точки Р на три взаимно перпендикулярные координатные оси. В зависимости от взаимного расположения положительных направлений координатных осей возможна правая (рис. 17, а) и левая (рис. 17, б) координатные системы.

В геометрических и кинематических исследованиях манипуляторов применяются правые прямоугольные, цилиндрические и сферические системы координат.

Более общую систему координат получают, задавая какие-либо семейства координатных поверхностей, таких, что через каждую точку пространства проходит по одной такой поверхности каждого семейства. Положения точки в такой системе определяется значениями параметров координатных поверхностей, проходящих через эту точку. Наиболее употребительные системы криволинейных координат – цилиндрическая и сферическая.

Ц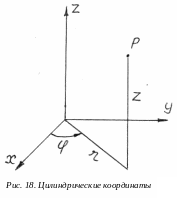 илиндрические координаты (рис. 18): r и  - полярные координаты проекции точки Р на основную плоскость (обычно XOY); z – аппликата - расстояние от точки Р доя основной плоскости. Для цилиндрических координат координатными поверхностями являются плоскости, перпендикулярные к оси Z (z=const); полуплоскости, ограниченные осью Z (=const), и цилиндрические поверхности, осью которых является ось Z (r=const). Координатные линии – линии пересечения этих поверхностей.

Сферические координаты (R – длина радиус-вектора,  - долгота,  - полярное расстояние) представлены на рис. 19. Если давать сферическим координатам значения в следующих пределах: , , , то получаются однозначно все точки пространства. Координатные поверхности – это сферы с центром в начале (R=const), полуплоскости, ограниченные осью Z (=const), конусы (с вершиной в начале), для которых ось Z является осью (=const). Координатные линии это линии пересечения этих поверхностей.

Связь между прямоугольными, цилиндрическими и сферическими координатами представлена в таблице формулами перехода, которые справедливы при следующих допущениях:

а) начала координат прямоугольной, цилиндрической и сферической систем совпадают: основная плоскость (Z=0) прямоугольной и цилиндрической систем совпадает с основной плоскостью (=0) сферической системы; линии отсчёта (=0)сферической и цилиндрической систем совпадают с осью х=0 прямоугольной системы. Оси OZ прямоугольной и цилиндрической систем совпадают;

б) отсчёт положительных значений  производится против часовой стрелки, если смотреть с положительного направления оси OY. Знак соответствует знаку координаты по оси OY.

Таблица 5

Связь между прямоугольными, цилиндрическими и сферическими

координатами

Система координат	Система координат
	Прямоугольная (x,y,z)	Цилиндрическая (r,,z)	Сферическая (R,,)
Прямоугольная (x,y,z)	x=x y=y z=z
Цилиндрическая (r,,z)		r=r = z=z
Сферическая (R,,)			R=R = =

Направление в пространстве характеризуется единичным вектором или его координатами – косинусами углов (рис. 20), образованных заданными направлениями с положительными направлениями осей координат (направляющие косинусы); при этом

l=cos; m=cos; n=cos; l²+m²+n²=1

Угол  между двумя заданными направлениями с направляющими косинусами l₁; m₁; n₁ и l₂; m₂; n₂ определяется из выражения cos= l₁l₂+ m₁m₂+ n₁n₂

Если два направления перпендикулярны, то l₁l₂+ m₁m₂+ n₁n₂=0.

П ереход от одной прямоугольной системы координат к другой прямоугольной системе координат можно осуществить при помощи параллельного переноса (до совмещения начала координат) и поворота системы относительно начала (до совмещения осей). Поворот прямоугольной системы координат можно описать с помощью направляющих косинусов, углов Эйлера, вектора конечного поворота, параметров Родрига-Гемильтона, параметров Кэли-Клейна и др.