Кинематический анализ манипуляторов методом проекций

Произведём анализ манипулятора типа «механическая рука», используемого для захвата и извлечения изделий из рабочей зоны и выдачи их на следующую позицию обработки.

Манипулятор робота представляет собой плоский механизм с захватом в точке Д. В заданной системе координат точка Д движется согласно уравнениям:

(38)

в течение 1с. На рис. 16 изображён в начальном положении механизм манипулятора и показаны положительные направления отсчёта углов , ,  и расстояния S. Размеры звеньев: а=1,30 м, b=1,10 м, с=0,55 м.

В начальный момент времени (t=0).

 =₀=62; =₀=33

Определить значения углов , ,  и расстояния S для указанного промежутка времени. Вычислить также угловые скорости , угловые ускорения , относительную скорость и относительное ускорение точки В. Вычисления произвести для моментов времени 0; 0,2; 0,4; 0,6; 0,8; 1с.

Для любого положения механизма справедливы векторные соотношения:

(39)

(40)

Г де (41)

Равенства (38)…(41) являются уравнениями связей, наложенных на систему. Спроецируем (39) и (40) на оси координат:

(42)

(43)

Продифференцировав (42) и (43) дважды по времени, учитывая (41), получим алгебраические уравнения относительно неизвестных угловых скоростей и скорости после первого дифференцирования и алгебраические уравнения относительно угловых ускорений и относительного ускорения , связывающие их между собой после второго дифференцирования.

(44)

(45)

(46)

Величины входящие в выражения (44) и (46) определяются дифференцированием уравнений движения схвата (38):

(47)

Для начального момента времени t=t₀=0 системы уравнений (44) и (45) имеют следующий вид:

(48)

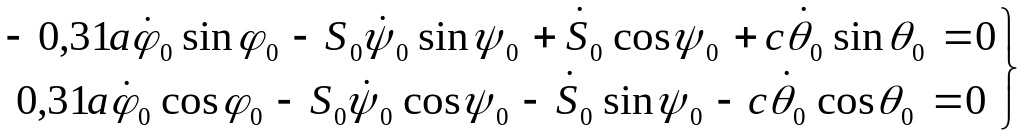(49)

Для определения S₀ и ₀ воспользуемся системой (43) для начального положения (t=0)

Разделив данную систему относительно S₀ и tg₀, получим

Подставляя значения a, b, c, ₀, ₀, ₀, S₀ в (48), (49), получим систему уравнений

Решая эту систему уравнений, получим:

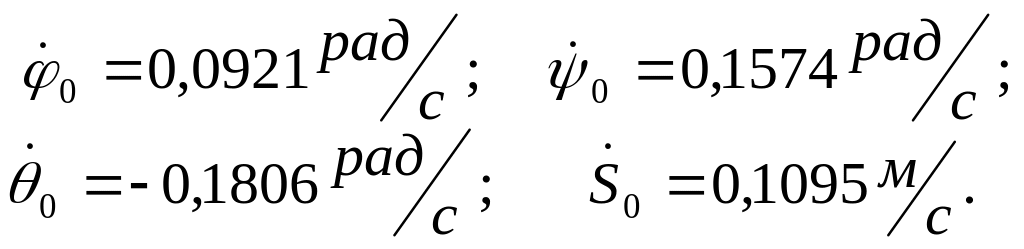(50)

Используя найденные результаты, составим систему для начального положения уравнений (46):

Решая эту систему уравнений, получим:

(51)

Следующий момент времени, при котором необходимо определить искомые величины, является t=t₁=t=0,2 с. Считая t малой величиной можно записать:

(52)

Выражение (52) непосредственно вытекает из разложения функций (t), (t), (t), S(t) в ряд Макларена в окрестности t=0. В результате вычислений:

В общем случае переход от _i, _i, _i, S_i к _i+1, _i+1, _i+1, S_i+1 будет осуществляться по формулам:

(53)

где i – порядковый номер рассчитываемого положения механизма. Уравнения (53) соответствуют закону изменения параметров , , , S в интервале времени [t_i, t_i+1] с постоянным ускорением (равномерное движение).

По найденным согласно (52) ₁, ₁, ₁, S₁ вновь строим системы уравнений (44) и (45) относительно неизвестных

Решая эту систему уравнений, получим:

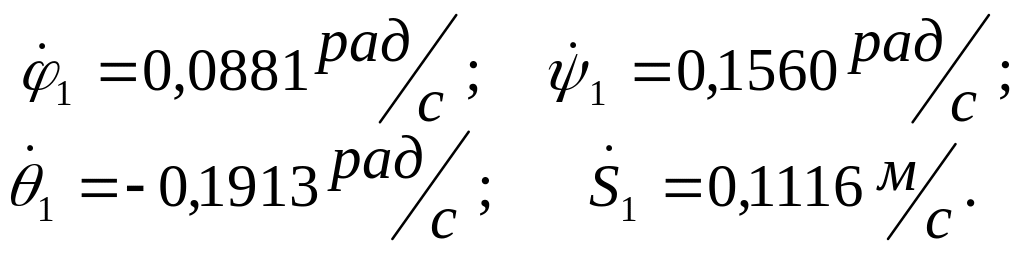
Используя полученные результаты, опять составляем системы уравнений (46) и (47) относительно неизвестных

Решая эту систему уравнений, получим:

Очередным моментом времени, при котором необходимо определить величины, является t=t₂=2t=0,4 с.

Воспользовавшись (53), при i=1 найдём ₂, ₂, ₂, S₂.

Описанная выше вычислительная процедура выполняется k раз, где

Здесь  - длительность процесса движения (=1с).

После проведения всех вычислений составляется таблица значений для всех различных моментов времени.