Плоские и пространственные цепи механизмов

В плоском механизме все подвижные звенья и их точки совершают движения в одной или параллельных плоскостях. В пространственном механизме звенья и их точки совершают движения в различных не параллельных плоскостях.

В ряде случаев манипулятор может быть плоским, но с целью повышения его маневренности и улучшения обслуживания захвату сообщаются дополнительные движения в разных плоскостях.

Число измерений структуры

Числом измерений N (Р) (или N-мерностью) механизма является количество типов взаимных связей различной физической природы, находящихся в нем и обеспечивающих нормальное функционирование системы: информационные, управляющие, логические связи.

Функциональные связи представляют собой твердые звенья механизмов и различные гидравлические, пневматические механизмы, обеспечивающие функциональные перемещения изделий. Функциональные связи со стойкой образуют структуру механизма.

Энергетические связи служат для обеспечения перемещения звеньев, выполнения логических операций, сбора и переработки информации, т.е. обеспечивают энергетическое питание всех звеньев и программно управляющей системы манипулятора.

Некоторые типы связей подразделяются на виды. Например, энергетические связи могут быть электрические, пневматические, гидравлические.

Для каждого измерения N-мерной системы обычно составляется своя структурная схема, устанавливающая номенклатуру задающих и исполнительных устройств или элементов, их относительное расположение, взаимные связи и функционирование. Общая структура механизма описывается многомерной матрицей смежности CN(Р), в которой каждый вид связей обусловливает сечение матрицы С_i. Чем больше число измерений структуры механизма, тем сложнее его общая структура.

Сложность структуры

Для механизма с разомкнутой структурой под сложностью понимают отношение:

где - сумма всех кинематических пар, входящих в цепь;

- сумма подвижных звеньев;

- число степеней свободы.

Структурная сложность плоского механизма (рис. 6) состоящего из р5 = 1, n = 1 и обладающего W = 1

Структурная сложность манипулятора (рис. 5):

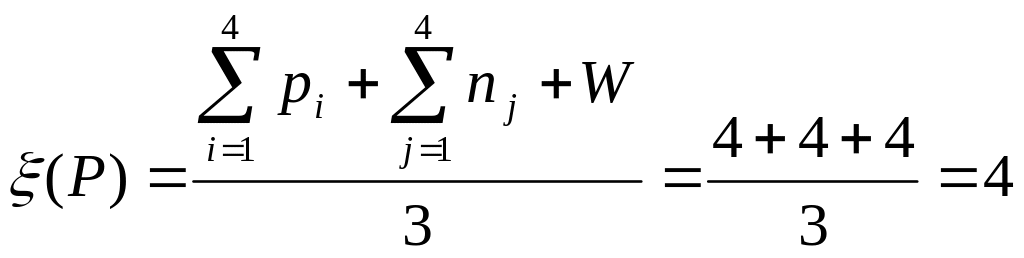
Структурная сложность манипуляторов с замкнутыми кинематическими цепями определяется в следующей последовательности:

1. размыкаются контуры;

2. выделяются все возможные варианты не замкнутых цепей и определяется структурная сложность каждого из вариантов;

3. производится суммирование _i(Р), полученная сумма и определяет сложность структуры манипулятора, т.е.

.

Для определения структурной сложности манипулятора (рис. 4) кинематическую цепь разомкнем путем разрыва связи S43. В результате получим две ацикличные цепи ABDEF и CD, значения сложностей которых и соответственно.

, поэтому

.

Структурная значимость кинематической пары

Для прогнозирования возможных последствий частичной потери подвижности пары необходимо знание величины критерия значимости пары. Структурную значимость кинематической пары в первом приближении можно оценить влиянием ее числа степеней свободы на общую подвижность манипулятора. Более точно и объективно значимость пары оценивается ее рангом .

Рангом называется величина, характеризующая структурную и функциональную значимость пары в кинематической цепи манипулятора. Для нахождения рангов пар используют комплексную матрицу смежности С_к, в которой диагональными элементами являются степени свободы кинематических пар , а не диагональные отображают локальные степени пар .

Ранг кинематической пары равен сумме членов строки матрицы

Более представительно характеризуют значимость удельные значения рангов пар q(p_i):

где - сумма элементов строки кинематической матрицы , соответствующая данной кинематической паре

- сумма всех элементов матрицы.

В качестве примера определим структурную значимость пар манипулятора (рис. 7).

1 . Устанавливаем, что цепь манипулятора описывается структурным множеством P(P, S)=P (3, 2) и выражением отношений . В цепи содержатся пары имеющие локальные степени

2. Составляем матрицу смежности кинематической цепи.

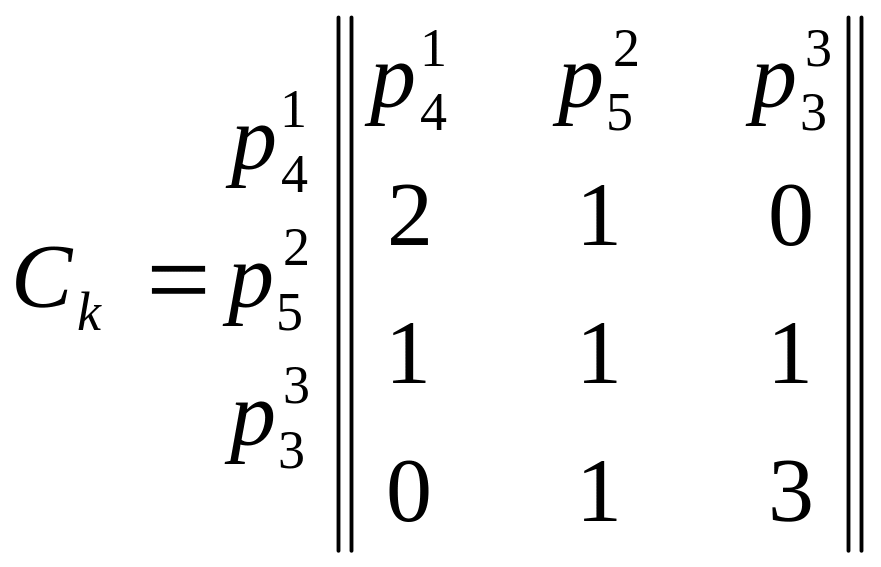
3. Определяем значение рангов.

=44

4. Вычисляем удельные значения рангов кинематических пар

Анализируя полученные значения q_i(p_i) следует отметить, что их величины соответствуют действительной значимости кинематических пар в функционировании манипулятора. Наибольший ранг имеет пара , что обусловливается не только числом её степеней свободы, но и положением в кинематической цепи. В случае выхода из строя пар манипулятор потеряет возможность перемещаться в направлении определенных осей координат, но будет обладать всеми возможными движениями захвата и тем самым выполнять функциональное назначение.