3.2. Проверка гипотезы о равенстве генеральных средних нормально распределенных генеральных совокупностей.

Проверка гипотезы о равенстве генеральных средних имеет важное практическое значение. Часто возникает ситуация, когда средний результат одной серии испытаний отличается от среднего результата другой серии испытаний. Возникает вопрос, можно ли различие средних объяснить случайной ошибкой эксперимента или оно обусловлено некоторыми закономерностями, воздействием некоторого фактора.

Проверка данной гипотезы осуществляется с помощью t-критерия Стьюдента. Критерий используется чаще всего в том случае, когда нужно проверить влияние какого-либо фактора на исследуемую величину.

• Если различие между выборочными средними статистически значимо, то фактор оказывает влияние на исследуемую величину.

• Если различие между средними незначимо, то фактор не оказывает влияния на исследуемую величину, различие между выборочными средними обусловлено воздействием случайных причин.

Применение t-критерия Стьюдента возможно как для зависимых, так и для независимых выборок.

Две независимые выборки.

В этом случае используется t-критерий Стьюдента для независимых выборок.

Проверка гипотезы осуществляется следующим образом:

1) выдвигаем гипотезы: (критерий имеет двустороннюю критическую область);

2) вычисляем наблюдаемое значение критерия по формуле:

;

3) по таблице критических точек распределения Стьюдента (двусторонняя критическая область) находим , где - уровень значимости, - число степеней свободы, .

4) сравниваем и , учитывая, что критерий двусторонний:

Если , то

Если ,

Замечание:

Две зависимые выборки.

В этом случае используется t-критерий Стьюдента для зависимых выборок.

В зависимых выборках сравнение величин и осуществляется с помощью величины , являющейся разностью между величинами и ( ).

Проверка гипотезы осуществляется следующим образом:

1) выдвигаем гипотезы: 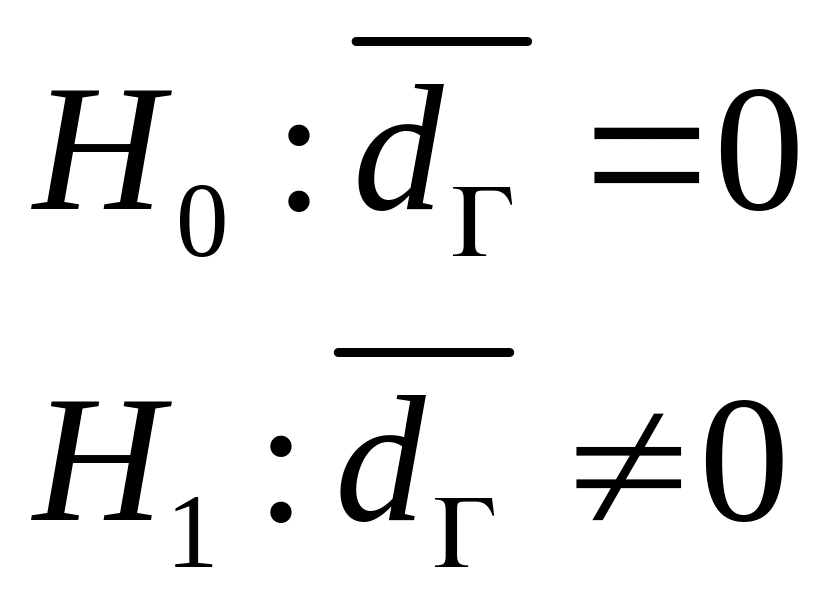, данные гипотезы соответствуют гипотезам . При таком виде конкурирующей гипотезы критерий будет иметь двустороннюю критическую область.

2) вычисляем наблюдаемое значение критерия по формуле: , где - вычисленная выборочная средняя ряда разностей, - стандартное отклонение ряда разностей, - объем выборки (зависимые выборки всегда имеют одинаковый объем, то есть ).

3) по таблице критических точек распределения Стьюдента (двусторонняя критическая область) находим , где - уровень значимости, - число степеней свободы, .

4) сравниваем и .

Если , то гипотеза отвергается, принимается гипотеза , следовательно, выборочные средние различаются значимо, генеральные средние в исследуемых совокупностях не равны между собой.

Если , то нет оснований отвергать гипотезу , следовательно, выборочные средние различаются незначимо, генеральные средние в исследуемых совокупностях равны.

Замечание:

Задача 1. Изучалось влияние тренировок на скорость сенсомоторной реакции спортсменов (в миллисекундах). Для этого случайным образом было отобрано 10 спортсменов. В таблице приведены значения изучаемого показателя до проведения тренировок и после них:

До тренировок	120	130	150	125	140	145	100	110	130	140
После тренировок	90	85	70	130	95	150	85	100	120	125

Установлено, что выборки извлечены из нормально распределенных генеральных совокупностей. Можно ли утверждать, что тренировки оказывают влияние на скорость сенсомоторной реакции спортсменов?

Решение: Так как выборки зависимы, извлечены из нормально распределенных генеральных совокупностей, решим задачу с помощью t – критерия Стьюдента для зависимых выборок.

1 этап. Предварительная статистическая обработка данных. Вычислим для всех столбцов таблицы.

№	1	2	3	4	5	6	7	8	9	10
до	120	130	150	125	140	145	100	110	130	140

Вычислим числовые характеристики выборки:

2 этап. Проверка гипотезы о равенстве генеральных средних.

а) выдвигаем гипотезы: .

б) наблюдаемое значение критерия: ;

в) по таблице критических точек распределения Стьюдента (двусторонняя критическая область) находим

г) , следовательно, гипотезу отвергаем, принимаем . Следовательно, генеральные средние не равны, выборочные средние различаются статистически значимо. Значит, при можно считать, что тренировки оказывают влияние на скорость сенсомоторной реакции спортсменов.

Вывод: При можно считать, что тренировки оказывают влияние на скорость сенсомоторной реакции спортсменов.

Задача 2. Изучалось влияние нового железосодержащего препарата на уровень гемоглобина при железодефицитной анемии. Контрольную группу составили пациенты, получавшие традиционный препарат, опытную – получавшие новый препарат. Результаты приведены в таблице.

Контрольная группа	98, 82, 93, 105, 98, 93, 101, 101, 93, 98
Опытная группа	98, 105, 108, 112, 98, 108, 112, 112

Можно ли при по результатам исследования сделать вывод, что исследуемый препарат вызывает повышение уровня гемоглобина в крови больных железодефицитной анемией. Установлено, что выборки извлечены из нормально распределенных генеральных совокупностей.

Решение: Так как выборки независимы, извлечены из нормально распределенных генеральных совокупностей, применим t-критерий Стьюдента для независимых выборок.

1 этап. Предварительная статистическая обработка данных.

2 этап. Проверка гипотезы о равенстве генеральных дисперсий.

а) выдвигаем гипотезы:

б) наблюдаемое значение критерия:

в) по таблице критических точек находим

г) , следовательно, нет оснований отвергать гипотезу , генеральные дисперсии равны. Значит, можно применять t-критерий Стьюдента.

3 этап. Проверим гипотезу о равенстве генеральных средних.

а) выдвигаем гипотезы:

б) наблюдаемое значение критерия:

в) по таблице критических точек распределения Стьюдента (односторонняя критическая область) находим

г) , следовательно, гипотезу отвергаем, принимаем . Следовательно, генеральные средние не равны, выборочные средние различаются значимо. Это различие обусловлено действием фактора. Значит, при можно считать, что исследуемый препарат вызывает повышение уровня гемоглобина в крови больных железодефицитной анемией.

Вывод: При можно считать, что исследуемый препарат вызывает повышение уровня гемоглобина в крови больных железодефицитной анемией.