
Практическая часть
Примеры построения графиков.
Построим график функции y = sin(x) на отрезке [-p p ] с шагом p /500:
x = -pi:pi/500:pi; y = sin(x); plot(y) % рис. а plot(x, y) % рис. б
График на рис. а отображает значения одномерного массива y, состоящего из 1001 элемента, как функцию от номера элемента; график на рис. б отображает значения того же массива как функцию элементов массива x.
(а) (б)
|
|
|
|
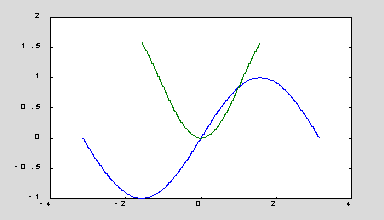
Рассмотрим различные способы применения функции plot(x, y) на примере графиков двух функций y1 = sin(x) и y2 = xsin(x):
x1 = -pi:pi/500:pi; y1 = sin(x1);
y2 = x1.*sin(x1); plot(x1',[y1' y2']) % рис. в plot( [y1' y2'], x1') % рис. г
(в) (г)


x2 = x1/2; y2 = x2.*sin(x2); plot([x1' x2'], [y1' y2']) % рис. д
|
(д) |
Построим график y = exp(x) в полулогарифмическом масштабе по оси y:
x = 0:0.1:100; semilogy(x, exp(x)) grid

|
Построим график функции rho = sin(2 * phi) * cos(2 * phi) в полярных координатах
phi = 0:0.01:2 * pi; polar(phi, sin(2 * phi). * cos(2 * phi))

Для построения графиков функций со значениями х и у, изменяющимися в широких пределах, нередко используются логарифмические масштабы.
» x=logspace(-1, 3);
» loglog(x,exp(x)./x)
» grid on
На рисунке представлен график функции ехр(х)/х в логарифмическом масштабе.
Неравномерное расположение линий координатной сетки указывает на логарифмический масштаб осей.

График с двумя осями ординат >> x=0:0.01:12*pi; >> plotyy(x,sin(x).*exp(-0.1.*x),x, 10*exp(-0.1.*x)) %

Трехмерная графика
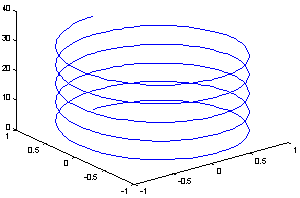
plot3(x,y,z) в тех же вариациях, что и plot, предполагает задание одномерных и двумерных массивов (строятся точки с координатами x(i,:),y(i,:),z(i,:) для каждого столбца и соединяются прямыми линиями. Если используется [x,y]=meshgrid(...), то строятся сечения.
>> t=0:pi/50:10*pi; |
>> [x,y]=meshgrid([-2:0.1:2],[-2:0.01:2]); |
>> plot3(sin(t),cos(t),t) % |
>> z=exp(-x.^2-y.^2); |
|
>> plot3(x,y,z) % |
|
|
Линии уровня
>> [x,y]=meshgrid(-8:0.5:8); |
>> [x,y]=meshgrid(-2:0.25:2); |
>> t=sqrt(x.^2+y.^2)+0.001; |
>> t=sqrt(x.^2+y.^2)+0.001; |
>> z=sin(t).^3./t; |
>> z=sin(t).^3./t; |
>> [c,h]=contour(x,y,z,20); |
>> [c,h,cf]=contourf(x,y,z,4); |
|
|
|
|
Заключение
MATLAB – высокоуровневая система программирования, позволяющая резко сократить затраты труда при проверке алгоритмов и проведении прикидочных расчетов. Возможность проведения больших расчетов на MATLAB'е определяется в основном теми затратами времени, на которые может пойти пользователь: здесь приходится выбирать между легкостью и наглядностью программирования и представления результатов, с одной стороны, и затратами времени на счет – с другой. Система очень удобна для освоения и апробации численных методов, что мы и хотим показать здесь прежде всего. Именно поэтому она рекомендуется как одна из основных для физиков и многих других естественно-научных специальностей в ведущих американских университетах. Детальное освоение любой большой программной системы – это достаточно длительный процесс, основу которого составляют индивидуальная работа, и наши занятия призваны дать лишь первоначальный импульс этому процессу в отношении MATLAB'а. Можно использовать программные и графические возможности системы для исследования численных алгоритмов.


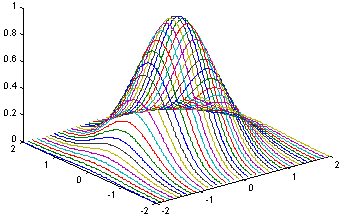



 Функция contour3(...) по
синтаксису полностью аналогична
contour(...), но изображает не проекции
линий уровня, а рисует их в пространственной
интерпретации; так
команда [c,h]=contour3(x,y,z,20); дает
фигуру.
Функция contour3(...) по
синтаксису полностью аналогична
contour(...), но изображает не проекции
линий уровня, а рисует их в пространственной
интерпретации; так
команда [c,h]=contour3(x,y,z,20); дает
фигуру.