5. Преобразование частоты

Преобразование частоты или гетеродирование – это сдвиг спектра радиосигнала по оси частот на определенное постоянное значение при сохранении его структуры. Процедура преобразования частоты связана с воздействием на НЭ двух напряжений: напряжения u_с(t) радиосигнала и напряжения вспомогательного генератора u_г(t) , называемого гетеродином.

При рассмотрении воздействия двух гармонических сигналов на НЭ (пункт 1.2) было показано, что в спектре тока НЭ помимо составляющих кратных частот присутствуют составляющие комбинационных частот, которые и используются при осуществлении преобразования частоты.

Принципиальная схема преобразователя частоты представлена на Рис. 2.4.

На вход преобразователя поступает сигнал:

u(t) =U_c(t)cosω₀t+U_гcosω_гt+U₀. (2.5)

где U_г , ω_г – соответственно амплитуда и частота гетеродина.

ВАХ транзистора аппроксимируется квадратичным членом степенного разложения:

I = a₂(u - U₀)² . (2.6)

Подстановка (2.5) в (2.6) после преобразований с использованием выше упоминавшихся тригонометрических соотношений дает:

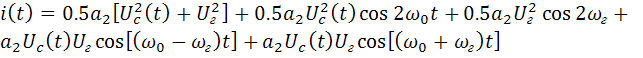. (2.7)

Из этого выражения следует, что составляющие разностной частоты:

, (2.8)

и суммарной частоты:

, (2.9)

с точностью до постоянного коэффициента повторяют закон изменения амплитуды радиосигнала , но на разностной и суммарной частотах. Таким образом, спектр радиосигнала без изменения его формы оказывается сдвинутым либо в область более низких , либо в область более высоких частот. При соответствующей настройке контура будет выделено напряжение полезного сигнала на соответствующей частоте.

Если - однотональный амплитудно-модулированный сигнал:

, (2.10)

то сигнал на выходе преобразователя на разностной частоте в соответствии с (2.8) будет иметь вид:

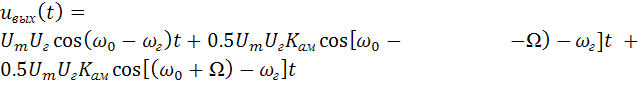. (2.11)

На Рис. 2.5 показаны спектры сигнала преобразователя при (Рис. 2.5,а) и при (Рис. 2.5,б).

Из (2.11) следует, что для увеличения амплитуды составляющих преобразованного сигнала следует выбирать .

Нелинейный элемент в составе преобразователя называется смесителем.

6. Формирование сигналов амплитудной модуляции

Как известно, амплитудно-модулированный сигнал описывается выражением:

, (2.12)

где – управляющий (модулирующий) сигнал; – коэффициент амплитудной модуляции; и – соответственно, амплитуда и частота несущего колебания.

Представив (2.12) в виде:

, (2.13)

нетрудно убедится в том, что амплитудно-модулированное колебание является результатом добавления к сигналу несущего колебания произведения управляющего сигнала и сигнала несущей. Таким образом, при построении амплитудных модуляторов основной задачей является реализация перемножения двух сигналов: управляющего сигнала и сигнала несущего колебания.

Эта задача решается с помощью нелинейного усилителя (Рис. 2.6), нагрузкой которого является колебательный контур, настроенный на частоту несущего колебания, и на вход которого поступает сигнал:

. (2.14)

Выбором напряжения смещения , обеспечим режим без отсечки тока (степенную аппроксимацию ВАХ транзистора):

. (2.15)

Подстановка (2.14) в (2.15) дает:

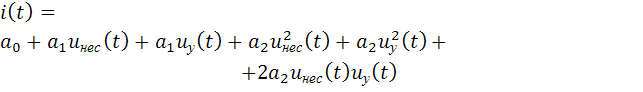. (2.16)

Разделив обе части (2.16) на получим:

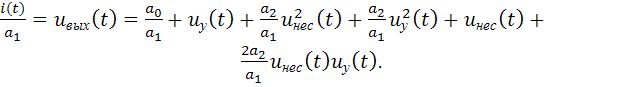(2.17)

Последние два слагаемых в (2.17) представляют собой в соответствии с (2.13) амплитудно-модулированный сигнал с коэффициентом , который выделяется на нагрузке усилителя:

(2.18)

При однотональной амплитудной модуляции:

.

Подстановка этого выражения в (2.18) после элементарных преобразований дает:

,

где – коэффициент амплитудной модуляции.

Режим без отсечки тока (степенная аппроксимация ВАХ) позволяет обеспечить .

Для обеспечения больших значений используют режим с отсечкой тока при аппроксимации:

, при . (2.19)

Подстановка (2.14) в (2.19) после преобразований дает:

,

где 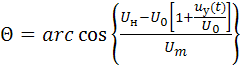– угол отсечки, изменяющийся в соответствии с изменением .

Амплитуда первой гармоники тока:

, (2.20)

также будет изменяться в соответствии с изменением , а следовательно и .

Амплитуда напряжения на выходе усилителя:

.

Важнейшей характеристикой модулятора является его модуляционная характеристика, т.е. зависимость амплитуды первой гармоники коллекторного тока транзистора от амплитуды управляющего сигнала, т.е. . Эта характеристика должна быть линейной в диапазоне изменений от минимального до максимального значений. Так как амплитуда первой гармоники зависит от угла отсечки как функция Берга [выражение (2.20)], то зависимость будет линейной в пределах линейного участка . Анализ графика зависимости (см. рекомендованную литературу) показывает, что эта зависимость имеет линейный характер в пределах . При этом функция Берга изменяется от до . Зная эти значения можно определить максимальное значение :

,

или подставляя в это выражения формулу (2.20):

.