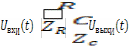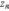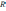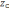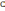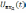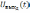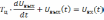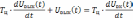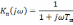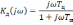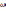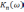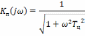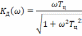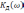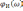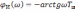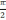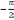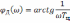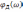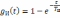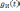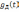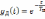3.1. Спектральный метод.

При рассмотрении характеристик линейной цепи было получено соотношение (5.10), связывающее спектральные характеристики входного и выходного сигнала с комплексным коэффициентом передачи цепи. Это соотношение лежит в основе спектрального анализа. Если задачей анализа является определение частотных характеристик выходного сигнала, то при известных 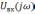и 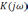использование (5.10) полностью решает эту задачу. В ряде случаев сигнал представлен во временной области и требуется найти отклик цепи как функцию времени. При этом спектральный метод анализа сводится к следующим операциям:

– для входного сигнала 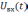прямым преобразованием Фурье находится комплексный спектр ;

– определяется комплексный коэффициент передачи цепи ;

– в соответствии с (5.10) определяется комплексный спектр выходного сигнала ;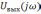

– обратным преобразованием Фурье вычисляется форма сигнала 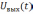на выходе цепи.

Итак, важнейшим условием использования спектрального метода является знание комплексного коэффициента передачи исследуемой цепи. Найти комплексный коэффициент передачи можно, используя методы теории цепей (метод узловых потенциалов или метод контурных токов). Наконец, цепь можно представить в виде делителя напряжения, элементами которого являются комплексные сопротивления

; ; .

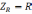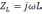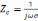Проиллюстрируем последний подход на примере RC-цепи. Если представить цепь как делитель напряжения, то выходной сигнал представляет собой напряжение на ёмкости С. Тогда, если 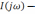комплексный ток, протекающий в цепи, то

,

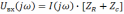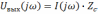
и комплексный коэффициент передачи

.

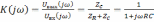4. Простейшие радиотехнические цепи.

4.1. Пассивные апериодические цепи.

При классификации радиотехнических цепей было отмечено, что по признаку наличия в цепи источника энергии цепи подразделяются на пассивные и активные. Начнем с рассмотрения пассивных цепей первого порядка, т.е. цепей содержащих один реактивный элемент (емкость или индуктивность). На основе этих цепей строятся как простейшие активные цепи, так и более сложные радиотехнические устройства.

Рассмотрим свойства наиболее часто встречающихся цепей – интегрирующей и дифференцирующей цепи.

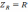
Определение характеристик цепей можно проводить любым из рассмотренных выше методов. Так, например, при определении частотных характеристик цепей в данном случае удобно представить ту или иную цепь в виде делителя напряжения, в состав которого входят комплексные сопротивления 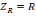и .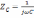

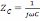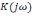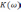
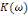В таблице 5 представлены схемы интегрирующей и дифференцирующей цепи, дифференциальные уравнения, которыми описываются цепи, аналитические выражения комплексного коэффициента передачи , амплитудно-частотных , фазо-частотных 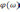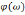, а также переходных 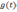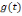и импульсных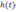 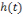характеристик и их графические изображения.

Анализ графиков АЧХ цепей показывает, что интегрирующая цепь пропускает нижние частоты и задерживает верхние, т.е. является фильтром нижних частот (ФНЧ). Дифференцирующая цепь наоборот пропускает верхние частоты и тем самым является фильтром верхних частот (ФВЧ).

Форма временных (переходной и импульсной) характеристик определяет характер переходных процессов. Для рассматриваемых цепей переходные характеристики представляют собой монотонно возрастающую (для интегрирующей цепи) и монотонно убывающую (для дифференцирующей цепи) функции. Это определило название цепей как апериодических.

Обратимся к выражению для комплексного коэффициента передачи интегрирующей цепи. При 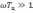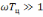комплексный коэффициент передачи

.

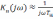Так как входной и выходной сигналы связаны соотношением

,

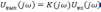то при указанном условии

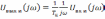. (5.40)

Но оператор 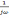является оператором интегрирования. Тогда применяя обратное преобразование Фурье, получим

,

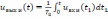т.е. цепь выполняет функцию интегрирования входного сигнала.

Аналогично для дифференцирующей цепи при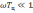

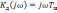
и 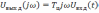(5.41)

Таблица 5

Интегрирующая цепь	Дифференцирующая цепь

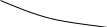
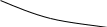
Как известно, оператор 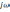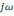– это оператор дифференцирования. Очевидно, обратное преобразование Фурье обеих частей (5.41) дает

.

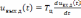
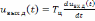Таким образом, рассмотренные простейшие RC-цепи осуществляют соответственно приближенное интегрирование и дифференцирование входных сигналов.

В заключение отметим, что в качестве интегрирующих и дифференцирующих цепей могут выступать и RL-цепи, где реактивными элементами являются индуктивности. Схемы этих цепей также представляют собой делители напряжения, с той лишь разницей, что в интегрирующей цепи выходной сигнал снимается с резистора, а в дифференцирующей – с индуктивности.