
- •Множество h является подгруппой группы g, если
- •Эти перестановки образуют четверную группу Клейна.
- •Формула Пойи для перечисления графов
- •2. Моделирование эволюции социума последовательностью вложенных подгрупп
- •В осточная (западная) модель
- •С еверо-Американская модель
- •3. Мера сложности, ее задание и примеры расчета Мера сложности
- •Задание меры сложности
- •Примеры расчета сложности
- •После применения формулы Стирлинга
В осточная (западная) модель
H3 H6 H12 H36
H3 H6 H12 H120
H3 H6 H18 H36
H4 H8 H16 H48
H4 H12 H36
H4 H12 H48
H6 H12 H36
H6 H12 H120
H6 H12 H48
H6 H18 H36
H6 H24 H48
H6 H24 H120
Так в представленном 6-вершинном графе отсутствует ребро 1-2, отображающее эффективную сельскохозяйственную интеграцию (животноводства и зерноводства), но присутствует ребро 3-4, воплощающее коллективистскую взаимопомощь в суровых природных условиях России. А далее на таком графе строится последовательность вложенных подгрупп.
К другим эволюционным возможностям приводит исходный граф для индейцев Северной Америки: здесь также отсутствует эффективная сельскохозяйственная интеграция, но кроме того отсутствуют и социальные свойства, воплощаемые ребром 3-4.
С еверо-Американская модель
H4 H12 H36
H4 H12 H48
H4 H8 H16 H48
На основе подхода, развитого в работах[1-5], строятся последовательности вложенных подгрупп, отображающие в определенном смысле оптимальные эволюционные траектории системы общественного воспроизводства, начиная с архаичного времени.
3. Мера сложности, ее задание и примеры расчета Мера сложности
Теперь, когда мы ввели понятие эволюционных цепочек подгрупп, можно вернуться к отправной точке нашего рассуждения. Исходя из того, что нам известно положение общества в текущий момент эволюции, т.е. нам известна группа перестановок, в которых циклирует система ЯВ, мы можем определить возможные пути эволюции общества, строя цепочки подгрупп (подполугрупп) над указанной исходной группой (полугруппой). Естественным образом возникает несколько вопросов. Например, по какому же пути пойдет развитие общества, если альтернатив несколько? Как нам известно: любой эволюционный переход связан с некоторыми инновациями, нововведениями, включающими в том числе и "правила запрета". Сами же инновации связаны с текущим уровнем развития общества, или, как мы будем говорить далее – сложностью СОВ. Таким образом, возникает еще один вопрос: как определить сложность СОВ? Нами был выбран подход, связанный с заданием сложности как меры на множестве групп перестановок.
Когда мера определена, мы можем вычислить ее для каждой подгруппы из полученных цепочек подгрупп. Далее, рассматривая разность5 мер соседних подгрупп, можем судить о возможности дальнейшей эволюции сообществ. Отдельно стоит отметить ситуацию, когда сложность эволюционного перехода велика, в таком случае можно говорить об эволюционном тупике в развитие общества. Эволюционный тупик – это невозможность перейти с одной ступени развития на следующую ступень, в силу большого разрыва между ними. Это можно интерпретировать, как невозможность примитивной социальной системы трансформироваться в значительно более развитую. Обязательно должны быть некоторые промежуточные стадии (периоды) развития, отображенные промежуточными группами на соответствующем графе.
Перейдем теперь непосредственно к введению меры сложности.
Задание меры сложности
Рассмотрим
некоторую группу перестановок
![]() ,
где k
– порядок группы. Нам необходимо ввести
меру сложности H(
).
,
где k
– порядок группы. Нам необходимо ввести
меру сложности H(
).
Положим, что сложность группы равна сумме сложностей каждой перестановки из этой группы:
![]() .
.
Для
вывода оценки сложности перестановки
будем использовать предложенный А.И.
Уемовым[3] подход для построения выражения
для субстратно-структурной сложности
систем. В указанном подходе используется
понятие энтропии. Напомним, что энтропия
вводится как мера неопределенности
случайной величины. Если задано конечное
множество
![]() - значений случайной величины
- значений случайной величины
![]() с распределением вероятностей
с распределением вероятностей
![]() ,
энтропией
называется величина:
,
энтропией
называется величина:
![]() .
.
При введении меры сложности мы учитывали следующие основные свойства энтропии:
 ;
;
 – принимает
минимальное значение равное нулю, если
– принимает
минимальное значение равное нулю, если
 ,
т.е. все значения
,
т.е. все значения
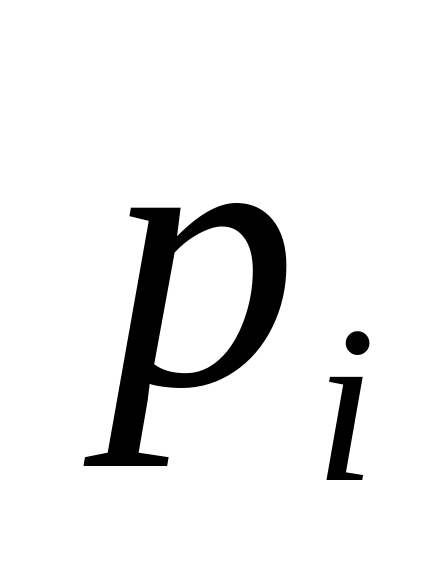 равны нулю, кроме одного, равного 1;
равны нулю, кроме одного, равного 1;
– принимает свое максимальное значение равное
 ,
если все
,
если все
 .
.
Запишем
перестановку в виде ориентированного
графа. Пусть этот граф имеет n
вершин. Рассмотрим произвольную вершину
графа, которую обозначим символом
![]() ,
где j=[1,n].
Из свойств перестановок будем иметь,
что эта вершина либо будет принадлежать
циклу, либо в этой вершине будет петля.
Теперь запишем типы бинарных отношений,
в которые может вступать эта вершина с
другими:
,
где j=[1,n].
Из свойств перестановок будем иметь,
что эта вершина либо будет принадлежать
циклу, либо в этой вершине будет петля.
Теперь запишем типы бинарных отношений,
в которые может вступать эта вершина с
другими:
1)
![]() - нет связи или, по-другому, нет маршрута
между парой вершин;
- нет связи или, по-другому, нет маршрута
между парой вершин;
2)
![]() - между вершинами существует маршрут
длиной один;
- между вершинами существует маршрут
длиной один;
…
n)
![]() - между вершинами существует маршрут
длиной (n-1).
- между вершинами существует маршрут
длиной (n-1).
Обозначим
символом
![]() те отношения
те отношения
![]() ,
где первым коррелятором является
.
Каждое из этих отношений имеет определенную
экстенсиональную длину на вершине
,
которую мы обозначим символом
,
где первым коррелятором является
.
Каждое из этих отношений имеет определенную
экстенсиональную длину на вершине
,
которую мы обозначим символом
![]() .
Т.к. каждая вершина может вступать не
более чем в (n-1)
отношение,
то будет выполнено равенство:
.
Т.к. каждая вершина может вступать не
более чем в (n-1)
отношение,
то будет выполнено равенство:
![]() .
.
Вероятность
того, что отношение
реализуется на вершине
,
обозначим
![]() .
Значение вероятности может быть
определено по формуле:
.
Значение вероятности может быть
определено по формуле:
![]() .
.
Здесь в числителе – фактическая, а в знаменателе – максимально возможная экстенсиональная6 длина отношения на вершине . При этом, как несложно видеть, выполняются следующие соотношения:
![]() ;
;
![]() .
.
Таким образом, энтропию, приходящуюся на вершину , можно задать следующей формулой:
![]() .
.
Суммируя теперь по всем вершинам, получим общую энтропию перестановки:
![]() .
.
Полученную величину можно рассматривать как меру сложности перестановки. Отметим несколько принципиальных свойств полученной меры и дадим им обоснование с точки зрения социологии:
 и
и
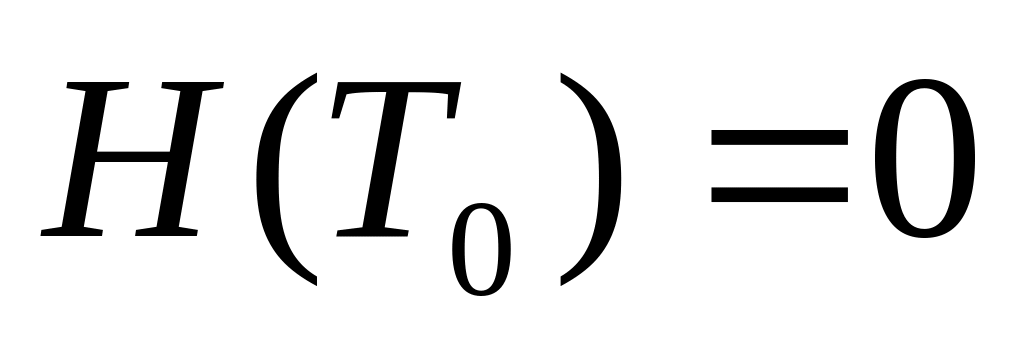 ,
где
- тождественная перестановка. Очевидно,
что сложность ВЦ, в котором нет связей
между ЯВ, должна быть минимальной.
,
где
- тождественная перестановка. Очевидно,
что сложность ВЦ, в котором нет связей
между ЯВ, должна быть минимальной.Чем больше средняя длина цикла в графе, тем больше сложность перестановки. Дадим социологическую интерпретацию этого свойства. Мы знаем что, чем больше длина цикла, тем больше ЯВ задействовано в едином обменном цикле. Совершенно очевидно, что ВЦ с максимальным задействованным числом ЯВ в нем, должен иметь большую сложность, т.к. СОВ в этом случае должна иметь больший эволюционный потенциал.
При уменьшении средней длины циклов в графе, также уменьшается величина сложности. Это удовлетворяет предположению, что система, разбитая на мелкие не связанные между собой группы ЯВ, имеет меньший эволюционный потенциал (сложность), чем единая система.
Отметим важную особенность полученной меры. При изменении числа вершин графа, т.е. при добавлении новых ЯВ, даже без добавления новых ребер будет изменяться величина сложности. Таким образом, при наращивании СОВ новыми ЯВ, перед сравнением сложностей в эволюционной цепи, необходимо делать пересчет сложности для предыдущих подгрупп.
Используя полученное выражение для H(T), мы можем записать меру сложности на группе H(G):
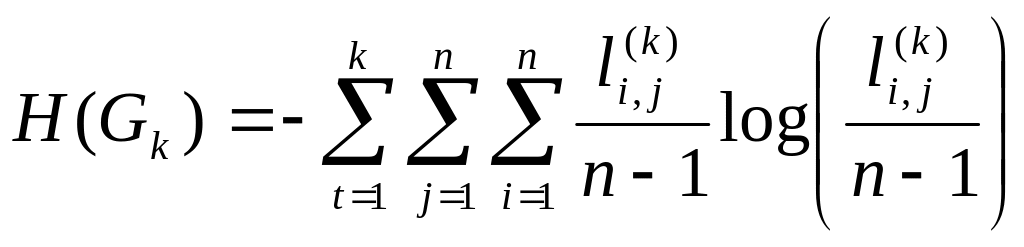 или
или
 .
.
Далее для краткости будем называть значение меры сложности просто «сложностью» или «структурной сложностью».
