Б.4. Фазовые соотношения и мощность в резистивном, индуктивном и емкостном элементах.

Элементами электрической цепи синусоидального тока являются:

• резистивный элемент (резистор), обладающий активным сопротивлением R;

• индуктивный элемент (индуктивная катушка без потерь) с индуктивностью L;

• емкостный элемент (конденсатор без потерь) с емкостью С.

Индуктивный элемент характеризуется величиной реактивного индуктивного сопротивления X_L =L = 2 f L

Емкостный элемент характеризуется величиной реактивного емкостного сопротивления

Сопротивления R, X_L, X_C имеют одинаковую размерность – Ом.

Проходящий по ним синусоидальный ток I создает на каждом из них падения напряжения, которые подсчитываются по закону Ома:

• для максимальных значений напряжений

U_Ма = I_М R;

U_МL = I_М X_L;

U_МС = I_М X_C;

• для действующих значений напряжений

U_а = I R;

U_L = I X_L;

U_C = I X_С,

где I_M и I - соответственно максимальное и действующее значение тока.

Из теории переменного тока известно, что:

• напряжение на активном сопротивлении U_а имеет одинаковую фазу с током I, проходящим через резистор R. В этом случае говорят, что напряжение и ток активного сопротивления совпадают по фазе (рис. Б.9а);

• напряжение на индуктивности U_L опережает ток I по фазе на 90° или, что то же самое, ток I отстает по фазе от напряжения U_L на 90° (рис. Б.9б);

• напряжение на емкости U_С отстает от тока I по фазе на 90° или, что то же самое, ток I опережает по фазе напряжение U_С на 90° (рис.Б.9в).

а) б) в)

Рис. Б.9. Токи и напряжения на сопротивлениях

Заметим, что на рис. Б.9 изображены действующие значения токов и напряжений, которые меньше максимальных значений в .

Указанные фазовые соотношения позволяют строить векторные диаграммы, что необходимо при расчете и анализе цепей синусоидального тока.

Для примера рассмотрим простейшую схему, состоящую из трех параллельно соединенных элементов: активного, индуктивного и емкостного (рис. Б.10). Положим нам известно напряжение U_AB и величины сопротивлений R, X_L, X_С , а также сопротивление линии R_Л.

Р ис. Б.10. Схема разветвлённой электрической цепи

По формуле закона Ома определим токи в ветвях:

Для нахождения тока I построим векторную диаграмму (рис. Б.11). С этой целью, выбрав произвольно направление U_AB, направим его на диаграмме, например, горизонтально вправо (в масштабе напряжений).

Рис. Б.11. Векторная диаграмма для цепи рис. Б.10

Векторы токов (Ī_а, Ī_L, Ī_C) выстраиваем в масштабе токов в соответствии с изложенными выше правилами:

• Ī_а совпадает по фазе с Ū_AB;

• Ī_L отстает на 90° от Ū_AB;

• Ī_C опережает Ū_AB на 90°.

Согласно первому закону Кирхгофа напишем уравнение:

в соответствии с этим уравнением произведем векторное сложение токов и найдем величину и направление тока в неразветвленной части цепи (Ī). Правила сложения векторов известны: к концу предыдущего слагаемого вектора пристраивается следующее слагаемое – вектор. Результирующий вектор Ī получаем, соединив начало координат с концом последнего пристроенного вектора (Ī_С).

Ток I можно определить аналитически по формуле теоремы Пифагора, рассматривая прямоугольный треугольник (рис. Б.11), образованный векторами токов.

В этом треугольнике один катет – ток I_а, другой катет (I_L - I_C), а ток I – гипотенуза, равная

Б.5. Активная, реактивная, полная мощность цепи однофазного синусоидального тока. Компенсация реактивной мощности

Рассмотрим мощности во всех элементах разветвленного участка АВ.

Мощность в активном сопротивлении R называется активной мощностью и обозначается буквой P = I_аU_AB = I_а ² R.

Единица измерения активной мощности Ватт (Вт). Активная мощность поступает от источника электрической энергии в активный элемент и преобразуется в нем в другие виды мощности (энергии), а именно: в тепловую, световую, механическую и т.д., и назад источнику не возвращается, рассеиваясь за пределами электрической цепи.

Активная мощность – это средняя мощность за период.

В индуктивном элементе (катушке с сопротивлением Х_L) поступившая от источника электрическая мощность (энергия) запасается в магнитном поле катушки (в одну четверть периода изменения тока – Т/4), а в следующую четверть периода вся запасенная катушкой энергия отдается назад источнику. Далее все повторяется, т.е. имеют место колебания энергии между источником электроэнергии и магнитным полем катушки. Амплитуда этих колебаний выражается величиной реактивной индуктивной мощности. В нашем случае

Q_L = I_LU_AB = I_L²X_L.

В емкостном элементе происходит аналогичный процесс обмена мощностями: мощность, переданная источником, сначала запасается в электрическом поле конденсатора за время Т/4, а в следующий такой же интервал времени отдается обратно источнику. Амплитуда колебания мощности характеризуется значением реактивной емкостной мощности

Q_C = I_СU_AB = I_C²X_C.

Таким образом, токи I_L и I_C не совершают полезной работы и обуславливают лишь колебания мощности между источником и реактивными элементами (X_L и X_C).

Эти токи поэтому называют реактивными:

• I_L – реактивный индуктивный ток;

• I_С – реактивный емкостный ток,

в отличие от I_а – активного тока.

Реактивные мощности Q_L и Q_С имеют разные знаки:

• реактивная индуктивная мощность Q_L – положительная;

• реактивная емкостная мощность Q_С – отрицательная.

Их алгебраическая сумма (т.е. с учетом знаков) называется суммарной реактивной мощностью Q = Q_L – Q_C.

Q, Q_L и Q_С имеют одинаковую размерность – вольтампер реактивный (вар).

Умножив все стороны треугольника токов (на рис. Б.11) на одну и ту же величину U_AB получим подобный треугольник мощностей (рис. Б.12), сторонами которого являются:

• прилежащий катет – активная мощность Р;

• противолежащий кадет – суммарная реактивная мощность участка АВ: Q = Q_L – Q_C;

• гипотенуза – полная мощность участка АВ

Рис. Б.12 Треугольник мощностей.

Единицей измерения полной мощности является вольтампер (В∙А). Полная мощность определяет величину тока I:

Ранее мы выяснили, что все полезные виды энергии, получаемые в результате преобразования электроэнергии в резистивном элементе (т.е. активном сопротивлении R), заключены в величине Р.

Из рис. Б.12 видно, что эти полезности могут быть получены при различных значениях угла φ, т.е. при различных значениях S.

При φ = 0 мощность S = P.

При больших значениях φ мощность S все больше будет превышать значение Р, так как увеличение угла φ возможно только с ростом реактивной мощности Q, а значит и S.

В подавляющем большинстве случаев в реальных системах электроснабжения ток I_L намного больше I_C, так как основные элементы электрических систем носят активно-индуктивный характер (генераторы, трансформаторы, двигатели – все имеют обмотки, т. е. содержат индуктивности). Поэтому угол φ велик, а S > P.

Чтобы уменьшить S, искусственно в схему вводят конденсаторы с целью увеличения Q_С, а значит – уменьшения суммарной реактивной мощности Q = Q_L – Q_C. При этом уменьшается полная мощность S, и, следовательно, ток I, который создает меньшие по величине потери мощности ∆P в тех элементах цепи, по которым он протекает.

Например, для схемы рис. Б.10 потери мощности в активном сопротивлении линии электропередачи R_Л будут равны:

∆P =I²R_Л.

Отношение называют коэффициентом мощности, а – оэффициентом реактивной мощности.

На практике стремятся за счет изменения (регулирования) реактивной мощности Q увеличить значение cosφ до уровня 0,92 ÷ 0,95, при этом коэффициент реактивной мощности близок к значению tgφ = 0,33.

Уменьшение величины реактивной мощности Q введением дополнительных реактивных элементов соответствующего знака (емкостных или индуктивных) называется компенсацией реактивной мощности.

Если в электрической системе имеет место избыток индуктивной мощности, то компенсация предполагает искусственное включение дополнительных емкостных элементов. Если же преобладает в системе емкостная мощность (что бывает значительно реже), то для компенсации вводятся дополнительные индуктивные элементы.

Компенсация реактивной мощности позволяет получить все те же полезности при меньшем значении токов и создаваемых ими потерь во всех элементах системы электроснабжения. Именно поэтому она является важнейшим мероприятием, обеспечивающим экономию электроэнергии, а значит сбережение энергетических ресурсов, которые используются на электростанциях для производства электроэнергии.

Б.6. Задания к самостоятельной работе.

Задание № 2

Заданы аналитические выражения для напряжения и тока:

В табл. Б.1 даны численные значения U_м, I_м, ω, ψ_u и ψ_i для каждого из 15-ти вариантов.

Необходимо выполнить следующее:

• написать выражение для фазы напряжения и тока.

• рассчитать действующие и средние значения напряжения и тока, их частоту (f), период (Т), угол сдвига фаз () между ними.

• построить волновые и векторные диаграммы, изобразив напряжение на волновой и векторной диаграмме в едином масштабе напряжений, а ток на обеих диаграммах в едином масштабе токов.

Изобразить на общей диаграмме ток и напряжение, обозначив на ней угол сдвига фаз () между ними.

Таблица Б.1

Параметр	№ варианта
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Uм, [В]	100	200	150	110	220	300	250	310	160	140	180	210	400	450	380
Iм, [A]	15	10	12	20	25	40	30	35	18	24	32	38	50	42	45
ω, [c-1]	314	628	942	314	628	942	314	628	942	314	628	942	628	314	942
ψu, [град]	120	-60	-120	60	30	150	-150	-90	-60	45	-60	90	60	30	-60
ψi , [град]	30	90	-30	-90	90	-120	90	150	-30	-90	45	-60	-45	120	150

Задание № 3

Заданы аналитические выражения трёх токов:

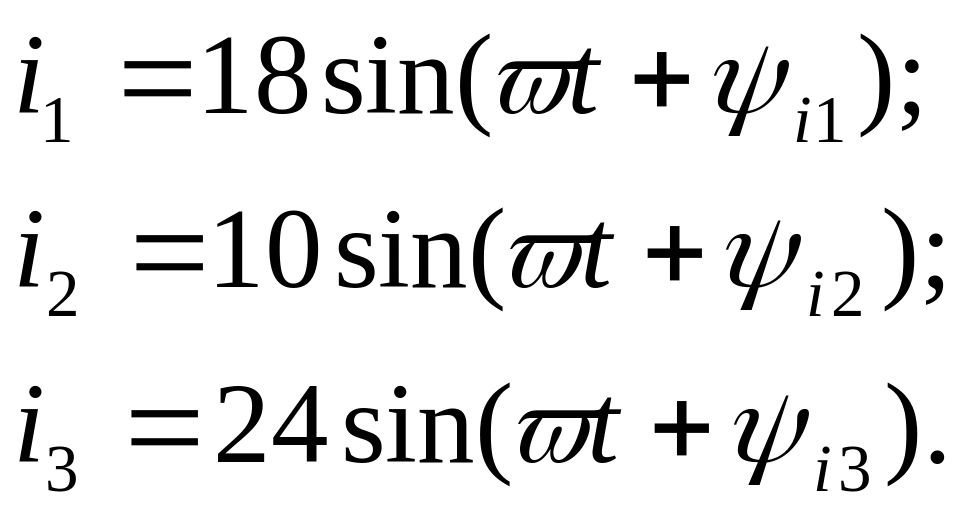
Углы начальных фаз токов представлены в табл. Б.2.

Таблица Б.2

Угол начальной фазы [град]	№ варианта
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
ψi1	120	60	90	30	0	150	60	120	30	90	-60	90	-30	0	30
ψi2	-30	-90	-60	-120	-150	60	0	30	-60	30	-150	-30	-120	-90	-60
ψi3	-60	-120	-90	-30	-60	30	-150	-60	-120	-150	60	-120	90	-120	-90

На векторной диаграмме, построенной в масштабе, изобразить векторы токов и обозначить углы их начальных фаз.

Определить расчётным путём углы сдвига фаз: ₁₂, ₂₃, ₁₃ и обозначить их на векторной диаграмме.

Отдельным построением получить на векторных диаграммах результирующие векторы от сложения и вычитания заданных векторов:

Примечание: все построения выполнить в масштабе.

Задание № 4

Выполнение этого задания имеет целью определение потерь электрической энергии в проводах, питающих активную, индуктивную и емкостную нагрузки.

Рассчитываются 2 режима работы.

Первый режим: выключатель «В» в схеме замещения (см. рис. Б.13) отключен, а это означает, что ветвь с ёмкостью отключена, то есть в схеме присутствует только активная (R) и индуктивная (X_L) ветви, по которым соответственно протекают токи I_а и I_L. Такой режим работы большинства существующих систем электроснабжения является самым распространённым. Действительно, в состав реальных систем электроснабжения предприятий различных отраслей промышленности (включая и лесные отрасли) входят наряду с активными потребителями (представленными в схеме замещения сопротивлением R) многочисленные индуктивные элементы (обмотки генераторов, двигателей, трансформаторов и др.), что отображается в схеме замещения индуктивным сопротивлением X_L. Таким образом, в первом режиме работы цепи нагрузка активно-индуктивная.

Второй режим: выключатель «В» включен, т.е. в схему вводится третья нагрузочная ветвь с емкостным сопротивлением X_С. Эту ветвь искусственно подключают с целью компенсации избытка индуктивности в нагрузке, что необходимо для снижения суммарной реактивной мощности в цепи. Говоря точнее, емкостную нагрузку включают с целью компенсации реактивной индуктивной мощности, что приводит к уменьшению тока (I) в неразветвлённой части цепи, а значит к уменьшению потерь мощности и электрической энергии в R_ЛЭП (т.е. в линии электропередачи).

В схеме электрической цепи заданы параметры I_а, I_L, I_с, U_АБ (см. табл. 4) и R_ЛЭП = 0,08 Ом, Т_ГОД = 8000 ч, С = 3,6 руб/кВт·ч.

Рис. Б.13

В задании требуется выполнить следующее:

1. Определить ток I в R_ЛЭП для двух режимов:

• выключатель «В» отключен;

• выключатель «В» включен,

предварительно построив на векторной диаграмме (обязательно в масштабе) U_АБ и токи в параллельных ветвях.

Рассчитать для этих двух режимов значения активной, реактивной и полной мощностей участка АБ (P, Q_L, Q_C, Q, S).

2. Построить треугольники мощностей для двух указанных режимов и уметь объяснять физический смысл всех мощностей, образующих построенные треугольники.

3. Вычислить потери мощности в R_ЛЭП для двух режимов (∆P' и ∆Р'') и определить соотношение ∆P'/∆Р''.

Примечание: ∆P = I²∙R_ЛЭП, где численное значение I для двух режимов взять из векторных диаграмм.

4. Сопоставить коэффициенты реактивной мощности (tgφ) каждого из режимов:

tgφ' и tgφ''.

5. Определить стоимость электроэнергии, теряемой в R_ЛЭП для обоих вариантов, имея ввиду что Т_год = 8000 часов (число часов работы в год), а С = 3,6 руб./кВт∙ч (стоимость 1 кВт∙ч).

Исходные данные к заданию № 4 представлены в табл. Б.3.

Таблица Б.3

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
UAБ	100	120	180	200	140	160	100	130	160	190	170	120	160	170	200
Iа	80	60	70	90	100	110	120	150	100	90	70	60	50	40	110
IL	170	100	180	130	150	140	170	140	130	70	60	100	40	80	100
IC	140	80	150	100	120	110	130	140	110	60	40	80	30	70	80

Б.7. Примеры выполнения заданий

Пример к заданию № 2

Даны аналитические выражения для напряжения и тока:

Из этих выражений выписываем параметры синусоидальных величин:

U_м = 300 В, I_м = 10 А;

ω = 628 с^-1;

ψ_u = 30º; ψ_i = – 60º.

Напишем выражения для

• фазы напряжения

• фазы тока

Рассчитаем действующее значения:

• напряжения

• тока

Рассчитаем средние значения:

• напряжения

• тока

Определим:

• частоту напряжения и тока из выражения для ω = 2πf, откуда

• период напряжения и тока

• угол сдвига фаз между напряжением и током

 = ψ_u – ψ_i = 30º – (–60º) = 90º.

Изобразим напряжение и ток на векторной и волновой диаграммах, выбрав предварительно масштаб: для напряжения в 1 см 100 В; для тока в 1 см 5 А.

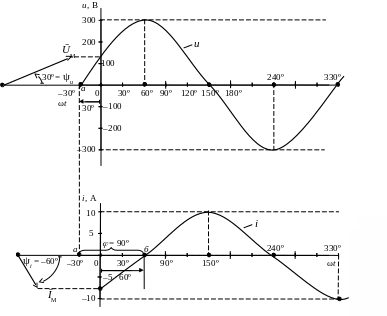
Рис. Б.14

Заметим, что масштаб при изображении угла синусоиды (по оси абсцисс) для кривых u и i должен быть один и тот же. В нашем случае принимаем, что в 1 см 30º, т.е.

(см. волновые диаграммы рис. Б.14).

Угол сдвига фаз () между векторами Ū_М и Ī_М находим на общей для Ū_М и Ī_М векторной диаграмме в результате её построения

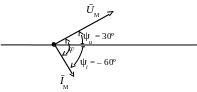
На волновой диаграмме угол  есть расстояние на оси абсцисс между точками а и б, где:

а – точка начала синусоиды u;

б – точка начала синусоиды i.

Пример к заданию № 3

Даны аналитические выражения для трёх токов:

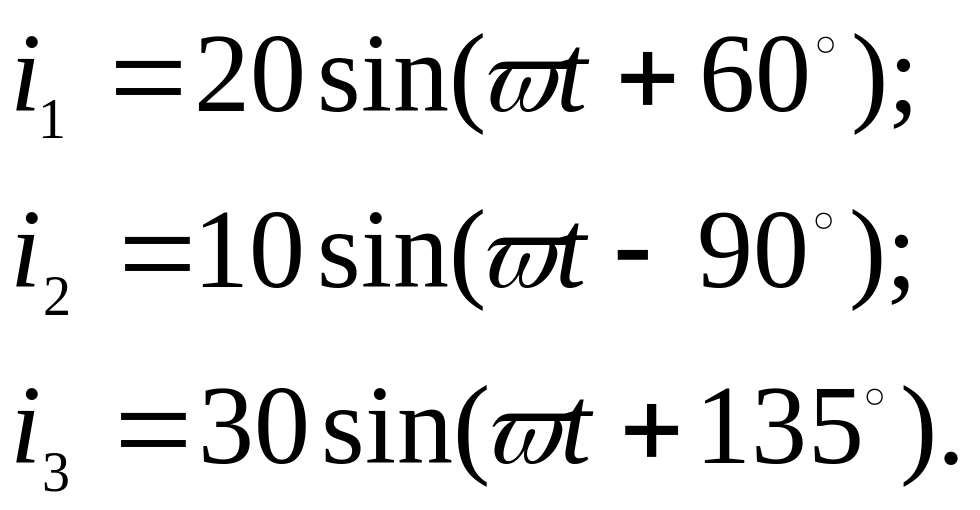
Из приведённых выражений следует, что амплитудные значения токов равны:

I_м1 = 20 А; I_м2 = 10 А; I_м3 = 30 А,

а углы начальных фаз составляют:

ψ_i1 = 60º; ψ_i2 = – 90º; ψ_i3 = 135º.

В

10А

1 см

ыбираем масштаб для токов и изобразим векторы заданных токов на векторной диаграмме, в 1 см 10 А,

Рассчитаем углы сдвига фаз:

• между первым и вторым током

₁₂ = ψ_i1 – ψ_i2 = 60º– (– 90º) = 150º;

• между первым и третьим током

₁₃ = ψ_i1 – ψ_i3 = 60º– 135º = –75º,

заметим, что знак «–» свидетельствует о том, что первый ток отстаёт по фазе от третьего тока на 75º.

• между третьим и вторым током

₃₂ = ψ_i3 – ψ_i2 = 135º– (– 90º) = 225º.

На векторных диаграммах найдём суммы и разности векторов токов:

• для (Ī_М1 + Ī_М2 + Ī_М3)

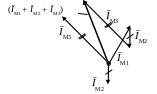
• для (Ī_М1 + Ī_М2)

• для (Ī_М1 – Ī_М2 – Ī_М3)

• для (Ī_М2 + Ī_М3 – Ī_М1)

Пример к заданию № 4

В приведённой электрической схеме (рис. Б.15) заданными являются следующие параметры:

I_а = 175 А;

I_L = 200 А;

I_C = 150 А;

U_AБ = 220 В;

R_ЛЭП = 0,1 Ом;

Т_ГОД =8000 ч;

С = 3,6 руб/кВт·ч.

Рис. Б.15

Рассчитаем ток в неразветвлённой части электрической цепи для двух режимов, обозначив:

I´ – ток 1-го режима;

I´´ – ток 2-го режима.

1-ый режим: выключатель «В» отключен, т.е. ток I_C = 0.

Напишем уравнение I закона Кирхгофа для точки А

Ī' – Ī_а – Ī_L = 0, откуда

Ī' = Ī_а + Ī_L.

Вектор Ī' получим как геометрическую сумму векторов Ī_а и Ī_L на векторной диаграмме.

Для построения векторной диаграммы выберем масштаб:

• для напряжения – в 1 см 40 В;

• для тока – в 1 см 50 А.

На рисунке:

• длина Ū_АВ = 5,5 см;

• длина Ī_а = 3,5 см;

• длина Ī_L = 4 см.

Согласно теории переменного тока вектор Ī_а совпадает по фазе с Ū_АБ, а вектор Ī_L отстаёт по фазе от Ū_АБ на 90º. Величину тока I' определим согласно теореме Пифагора как гипотенузу прямоугольного треугольника, катетами которого являются токи I_а и I_L.

2-ой режим: выключатель «В» включен, т.е. по ветви протекает ток I_C = 150 А.

Определим ток I" в неразветвлённой части цепи, написав уравнение I закона Кирхгофа для точки А схемы с тремя параллельными ветвями:

Ī" – Ī_а – Ī_L – Ī_С = 0, откуда

Ī" = Ī_а + Ī_L + Ī_С,

т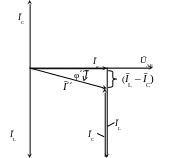 .е. на векторной диаграмме вектор Ī´´ найдем как геометрическую сумму трёх векторов (Ī_а, Ī_L, I_C). При выбранном ранее масштабе длина вектора I_C равна 3 см.

На векторной диаграмме I_С опережает по фазе напряжение Ū_АБ на 90º. Ток I" рассчитаем по формуле теоремы Пифагора из треугольника токов, катетами которого являются ток I_а и разность токов (I_L – I_С)

Рассчитаем активную, реактивную и ёмкостную мощность нагрузочного участка АБ.

Активная мощность:

• в режиме 1 и 2 её величина одна и та же

Р_АБ = U_АБ · I_а = 220 · 175 = 38500 Вт = 38,5 кВт.

Реактивная индуктивная мощность:

• в режиме 1 и 2 её величина также остаётся неизменной

Q_{L АБ} = U_АБ · I_L = 220 · 200 = 44000 вар = 44 квар.

Реактивная ёмкостная мощность:

• в режиме 1

Q_{С АБ} = 0.

• в режиме 2

Q_{С АБ} = U_АБ · I_С = 220 · 150 = 33000 вар = 33 квар.

Суммарная реактивная мощность участка АБ:

• в режиме 1

Q_АБ = Q_{L АБ} = 44 квар.

• в режиме 2

Q_АБ = Q_{L AБ} – Q_{C AБ} = 44 – 33 = 11 квар.

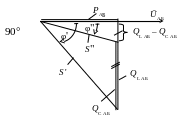
Полная мощность участка АБ:

• в режиме 1

• в режиме 2

Построим треугольники мощностей для обоих режимов, выбрав предварительно масштаб мощности: в 1 см – 10 (кВт, квар, кВ·А).

Треугольники мощностей получим умножением сторон треугольников токов (на предыдущих векторных диаграммах) на напряжение U_АБ.

Рассчитаем потери мощности в сопротивлении линии электропередачи (R_ЛЭП) для двух режимов.

1-й режим:

∆Р' = (I')² · R_ЛЭП = 266² · 0,1 = 7075,6 Вт ≈ 7,1 кВт.

2-й режим:

∆Р" = (I")² · R_ЛЭП = 182² · 0,1 = 3312,4 Вт ≈ 3,3 кВт.

Их соотношение:

т.е. потери мощности в режиме 2 (после подключения компенсирующего устройства) уменьшились более чем в 2 раза.

Коэффициенты реактивной мощности будут равны (см. треугольники мощностей)

что связано с изменением угла сдвига по фазе со значения ' до величины ".

Определим стоимость электроэнергии, теряемой за год в линии электропередачи (т.е. в R_ЛЭП) в обоих режимах:

Э' = ∆Р' · Т_ГОД · С = 7,1 · 8000 · 3,6 = 204480 руб.

Э" = ∆Р" · Т_ГОД · С = 3,3 · 8000 · 3,6 = 95040 руб.

Таким образом стоимость годовых потерь в результате компенсации реактивной мощности в электрической системе снизилась в 2,15 раза, что в абсолютном выражении составило

Э' – Э"= 204480 – 95040 = 109940 руб.  110 тыс. руб.