2.5 Полоса пропускания оптического волокна

Многие производители волокна и оптических кабелей не используют в спецификации дисперсию в многомодовых изделиях. Вместо этого указывают произведение полосы пропускания на длину линии. Полоса пропускания в означает возможность передачи сигнала в полосе на расстояние 1км, что также означает, что произведение максимальной частоты сигнала на длину передачи может быть меньше или равна 400. Можно передавать сигнал более низкой частоты на большие расстояния или более высокой частоты на меньшее расстояние (рисунок 2.12).

Рисунок 2.12 – Зависимость длины передачи от ширины полосы пропускания для волокна

Полоса пропускания (рабочая полоса частот) определяет объем информации, который можно передать по ОК. На рисунке 2.13 показан характер изменения дисперсии и пропускной способности ОВ в зависимости от длины линии.

Снижение из-за дисперсии величины до допустимого значения минимизирует дальность передачи по ОК.

Рисунок 2.13

При расчете полосы пропускания можно воспользоваться формулой:

.

Контрольные вопросы:

- Что такое числовая апертура? Свойства. Формулы для нахождения.

- Основные геометрические и оптические параметры волокна.

- Что такое нормированная частота? Её значение.

- Определение количества мод.

- Принцип распространения сигнала в ступенчатых оптических волокнах.

- Принцип распространения сигнала в градиентных оптических волокнах.

- Виды потерь в ОВ.

- Собственные потери ОВ. Определение, формулы для нахождения.

- Дополнительные потери ОВ. Определение, виды.

- Материальная дисперсия. Определение, формулы для нахождения.

- Модовая дисперсия градиентных ОВ. Определение, формулы для нахождения.

- Волноводная (внутримодовая ) дисперсия. Определение, формулы для нахождения.

- Что такое полоса пропускания? Зависимость полосы пропускания ОВ от дисперсии.

3 Оптические соединители

Для соединения элементов ВОСП между собой требуются простые и надежные соединители световодов друг с другом (ОВ – ОВ), с излучателями (ИИ – ОВ), с фотодетекторами (ОВ – ФД).

Оптические соединители (ОС) представляют собой один из самых ответственных классов пассивных компонентов для ВОСП. От их качества зависят предельные возможности и сроки эксплуатации. Совокупность требований, предъявляемых к ОС, может быть сформулирована следующим образом:

- малые оптические потери;

- стабильность параметров в процессе эксплуатации;

- устойчивость к внешним механическим и физико-химическим воздействиям;

- надежность и простота соединений;

- низкая стоимость

– герметичность.

3.1 Оптические потери при непосредственном (торцевом) соединении волоконных световодов

Эти потери можно разделить на три группы:

- потери, определяемые взаимным расположением оптических волокон в соединителях (радиальное смещение торцов, угловое рассогласование, осевое рассогласование, неперпендикулярность торцов относительно оси ОВ);

- потери, связанные с отражением от торцов ОВ;

- потери, связанные с неидентичностью параметров соединяемых волоконных световодов.

Потери в результате радиального смещения (децентровка) могут быть определены как:

,

где - коэффициент эффективности совмещения, зависящей от децентровки, профиля показателя преломления ОВ, модового состава оптического излучения. Коэффициент эффективности совмещения зависит от относительного радиального смещения ( –смещение, –радиус сердцевины), а также от модового состава излучения и распределения оптической энергии по сечению световода (рисунок 3.1).

Рисунок 3.1

Для волоконных световодов рассчитывается по формулам:

- со ступенчатым профилем показателя преломления и однородного возбуждения мод;

- со ступенчатым профилем показателя преломления и учетом мод оболочки;

- с градиентным профилем показателя преломления и однородного возбуждения мод;

- с градиентным показателем преломления и учетом мод оболочки.

Для волоконных световодов с градиентным профилем показателя преломления оптические потери выше. Это связано с тем, что их числовая апертура, максимальна на оси и убывает до нуля к периферии сердцевины.

Для одномодовых волокон более точно оптические потери в результате децентровки рассчитываются по формуле:

,

где w – параметр, определяющий диаметр луча (модового пятна)

Угловое рассогласование волоконных световодов также приводит к существенным оптическим потерям, но в меньшей степени, чем децентровка. Для многомодовых волоконных световодов можно использовать формулу:

где - показатель преломления сердцевины;

- показатель преломления среды между сердцевины;

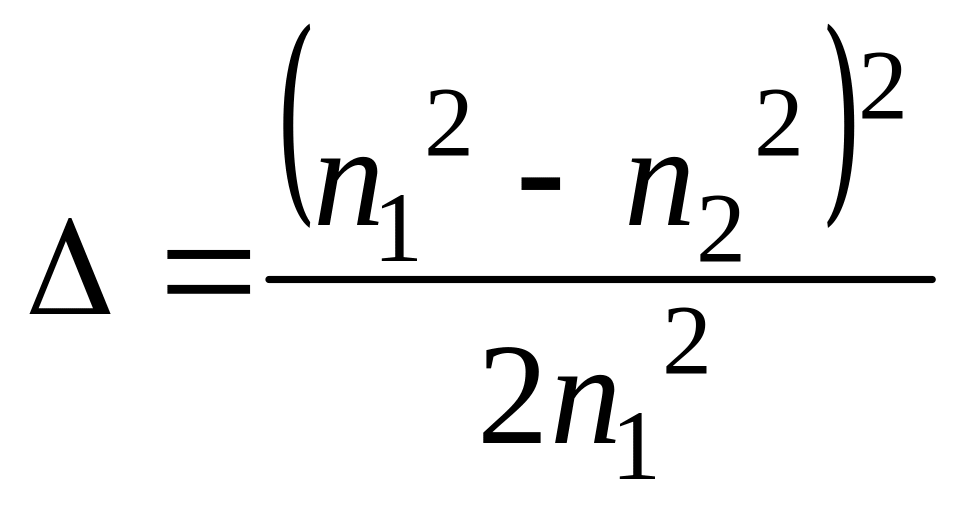- относительная разность показателей преломления сердцевины и оболочки;

- угол рассогласования, рад (рисунок 3.2).

Рисунок 3.2

Для одномодовых волоконных световодов оптические потери могут быть рассчитаны по уравнению:

.

Осевое рассогласование также увеличивает оптические потери (рис.3.3).

Рисунок 3.3

Для многомодовых волокон потери равны:

,

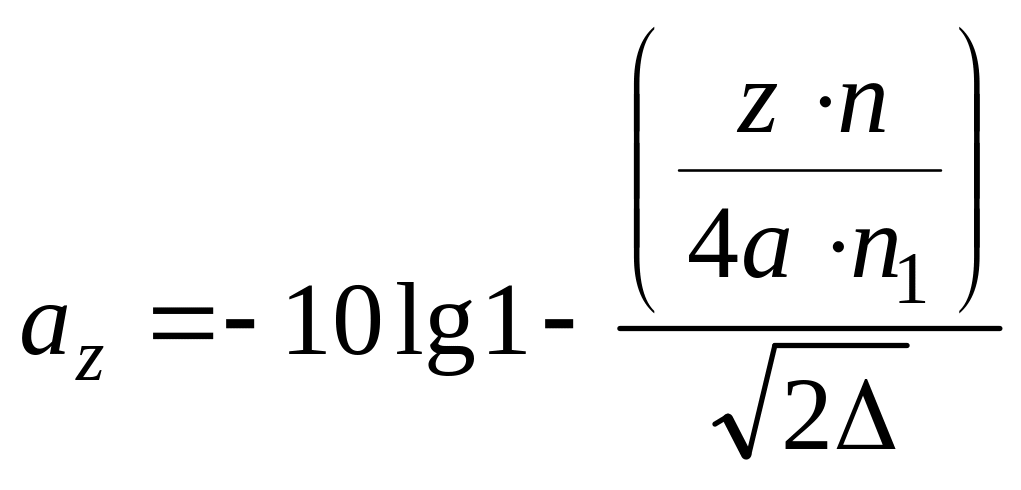где - показатель преломления среды между торцами;

- расстояние между торцами ОВ.

Для одномодовых волокон потери определяются:

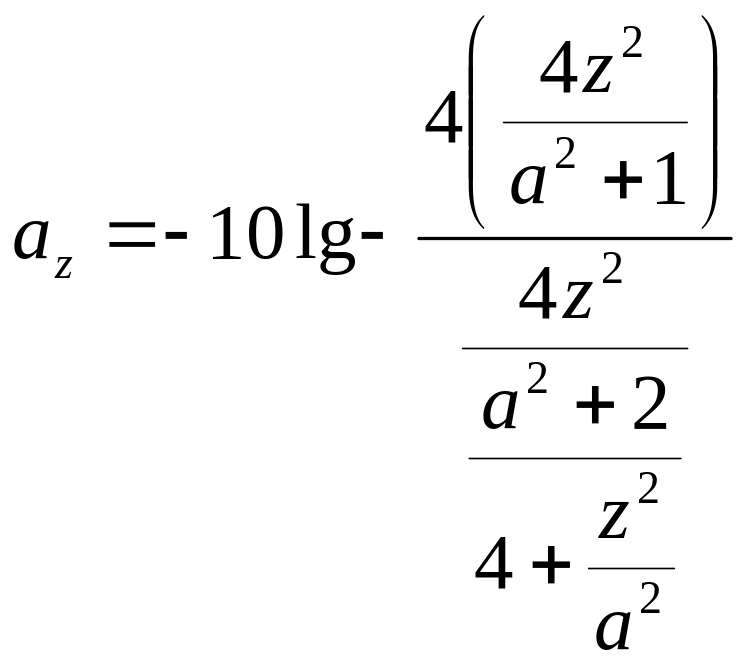
Перпендикулярность торцов относительно оси (рисунок 3.4а) и кривизна поверхности торцов (рисунок 3.4б) при соединении ОВ вносят оптические потери, определяемые по формулам:

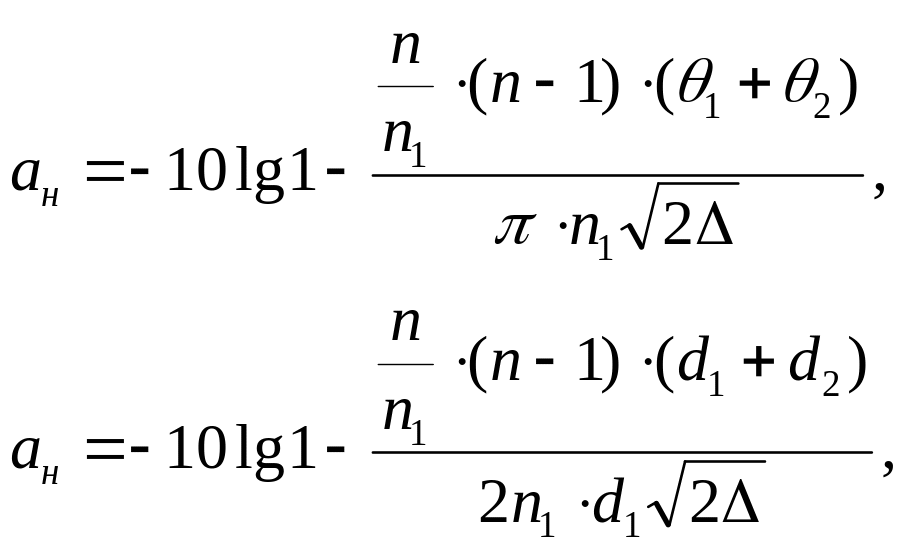
где и - угловые отклонения поверхности торцов;

и - диаметры скругленных поверхностей торцов (рисунок 3.4)

Рисунок 3.4

Все вышеперечисленные потери определяются конструкцией оптических соединительных устройств и технологией их изготовления.

Отражение оптического излучения от торца волокна из-за несоответствия показателей преломления сердцевины волокна и среды в зазоре между торцами (френелевские потери) определяют по формуле:

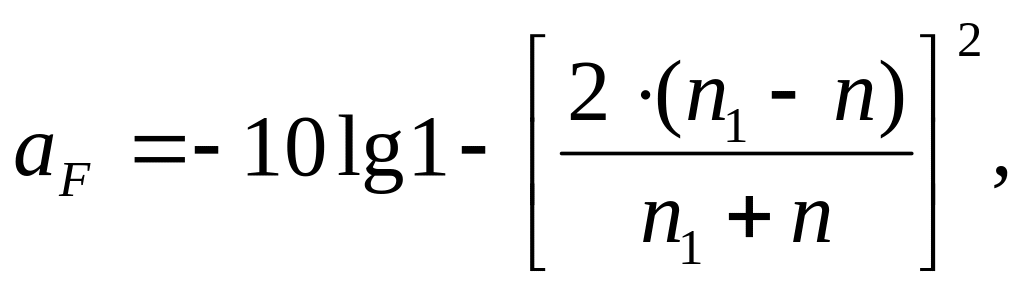
где и - показатели преломления сердцевины и среды между торцами волокон соответственно.

Оптические потери, связанные с неидентичностью параметров соединяемых световодов (рисунок 3.5) возникают из-за различия модового состава световодов и могут быть рассчитаны по формулам:

- при отличии диаметров ОВ:

- при отличии апертур;

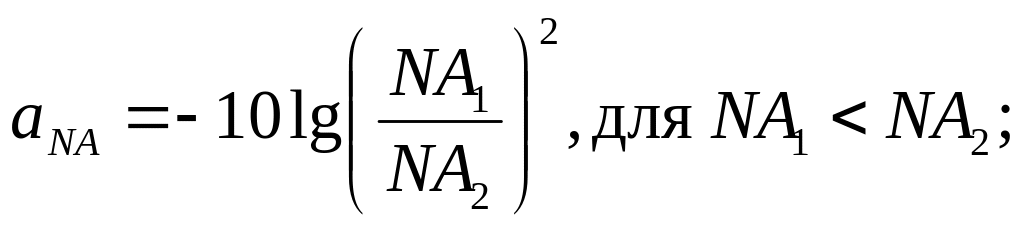
- при отличии индексов, определяющих профиль показателя преломления:

.

Рисунок 3.5