
Решение задания 4:
Дискретизация – представление непрерывного сигнала эквивалентной ему по информационному содержанию последовательностью дискретных отсчетов (выборок).
Квантование – придание величинам импульсов «округленных» (квантованных) значений, то есть, формирование дискретного и по уровню сигнала из дискретного по времени.
Представим заданный непрерывный сигнал в виде сигнала ИКМ.
Рассчитаем интервал дискретизации ∆t по формуле:
 c.
c.
Построим непрерывный сигнал u(t), плавно меняющийся во времени по своим исходным данным через интервал времени равным ∆t.
Определим количество уровней квантования по формуле:
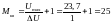 .
.
Определим число разрядов в кодовой комбинации:
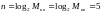
Определим квантованные значения Uкв (t) дискретного сигнала для каждого из остчетов, если Uкв (t) не равно целому числу, то его нужно округлить до ближайшего целого большего числа
Определим порядковый номер уровня квантования для каждого из отсчетов по формуле:
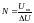 .
.
Закодируем номера уровней квантования N пятиразрядным двоичным кодом. Результаты сведем в таблицу 6.1.
Таблица 6.1 – Результат квантования
t |
1 |
2 |
3 |
4 |
5 |
6 |
Ut, мВ |
10 |
5,6 |
11,6 |
23,7 |
18,6 |
9,7 |
Uкв, мВ |
10 |
6 |
12 |
24 |
19 |
10 |
N |
10 |
6 |
12 |
24 |
19 |
10 |
Код |
1010 |
110 |
1100 |
11000 |
10011 |
1010 |
Теорема В.А. Котельникова формулируется следующим образом: если непрерывный сигнал u(t) имеет ограниченный спектр и наивысшая частота в спектре меньше, чем fв герц, то сигнал u(t) полностью определяется последовательностью своих мгновенных значений в дискретные моменты времени, отстоящие друг от друга не более чем на 1/(2fв) секунд.
Другими словами период дискретизации должен хотя бы в два раза меньше периода наивысшей частотной составляющей спектра непрерывного сигнала, т.е. на каждый период наивысшей частотной составляющей должно приходиться по крайней мере два отсчёта (выборки).
Задание 5
Дайте определение понятия «длинная линия»
Приведите эквивалентную схему 1 км длинной линии.
Дайте определение бегущей, стоячей и смешанной волн в длинной линии.
Рассчитайте коэффициент отражения для Z н = ∞; Z н = О;
Zн = ЈXн; Zн = Zв, коэффициент бегущей и стоячей волн, входное сопротивление отрезков линии длиной кратной λ/4, передаваемую мощность сигнала в линии.
Постройте графики изменения напряжения и тока вдоль длины линии при Zн=∞; Zн =0;
Поясните, каким образом можно согласовать две линии с разными сопротивлениями.
Исходные данные в таблице 5.
Таблица 5
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Zв, Ом |
50 |
75 |
100 |
150 |
200 |
300 |
400 |
800 |
1600 |
3200 |
Zн, Ом |
65 |
40 |
120 |
165 |
230 |
260 |
380 |
930 |
1400 |
3500 |
Pmax, мВт |
10 |
5 |
15 |
20 |
40 |
50 |
60 |
30 |
25 |
18 |
