ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

ХАБАРОВСКИЙ ИНСТИТУТ ИНФОКОММУНИКАЦИЙ

(ФИЛИАЛ)

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО

ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ОБРАЗОВАНИЯ

«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ»

Специальность: 11.02.11 Сети связи и системы коммутаций

ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА №1

по дисциплине

«Теория электросвязи»

Вариант	1
Выполнил
(ФИО)
2			курс			ПССиСК		группа
			шифр
Проверил
			(ФИО преподавателя)
Отметка
		(зачтено/незачтено)					дата проверки

Хабаровск 2017 г.

СОДЕРЖАНИЕ

Задание №1	3
Задание №2	6
Задание №3	7
Задание №4	11
Задание №5	14
Список использованной литературы	19

Задание 1

1. Дайте определение понятия сигнал. Перечислите физические параметры сигнала и их физический смысл.

2. Дайте определение сигналам: аналоговый и дискретный, периодический и непериодический, детерминированный и случайный. Приведите примеры.

3. Начертите временные диаграммы периодических сигналов прямоугольной формы с заданными параметрами в таблице 1.

4. Рассчитайте спектральный состав таких сигналов и постройте спектральные диаграммы для них.

5. Поясните, от каких факторов зависит спектральный состав периодических сигналов прямоугольной формы.

6. Укажите ширину спектра для каждой последовательности импульсов и поясните, отчего она зависит

Таблица 1

Параметры сигнала	Вариант
	1	2	3	4	5	6	7	8	9	10
Амплитуда Um, В	6	8	12	10	24	20	18	22	15	14
Период Т, мС	12	116	110	18	224	20	30	336	32	28
Длительность импульса первого сигнала tu1, мС	4	8	2	3	6	5	6	6	8	7
Длительность импульса второго сигнала tu2, мС	3	4	5	6	8	4	5	12	4	14

Решение задания 1:

Сигнал – носитель информации, используемый для передачи сообщений в системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением.

К параметрам сигналов относятся:

- Мощность сигнала: ;

- Удельная энергия сигнала, определяется как интеграл от мощности по всему интервалу существования или задания сигнала: ;

- Длительность сигнала T – определяет интервал времени, в течение которого сигнал существует (отличен от нуля);

- Динамический диапазон есть отношение наибольшей мгновенной мощности сигнала к наименьшей: ;

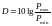- Ширина спектра сигнала F – полоса частот, в пределах которой сосредоточена основная энергия сигнала;

- База сигнала есть произведение длительности сигнала на ширину его спектра B=TF. Необходимо отметить, что между шириной спектра и длительностью сигнала существует обратно пропорциональная зависимость: чем короче спектр, тем больше длительность сигнала. Таким образом, величина базы остается практически неизменной;

- Отношение сигнал/шум равно отношению мощности полезного сигнала к мощности шума;

- Объём передаваемой информации характеризует пропускную способность канала связи, необходимую для передачи сигнала. Он определяется как произведение ширины спектра сигнала на его длительность и динамический диапазон: V=FTD.

Аналоговый сигнал– изменяющийся непрерывно во времени и принимающий любые значения на некотором интервале сигнал. Аналоговые сигналы описываются некоторой математической функцией времени. Пример АС — гармонический сигнал: s(t) = A·cos(ω·t + φ).

Дискретный сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени t_i (где i — индекс). Обычно промежутки времени между последовательными отсчётами (Δt_i = t_i − t_i−1) постоянны; в таком случае, Δt называется интервалом дискретизации. Сами же значения сигнала x(t) в моменты измерения, то есть x_i = x(t_i), называются отсчётами.

Сигнал s(t) называется периодическим, если он точно повторяет свои значения через одинаковые промежутки времени. При этом наименьший интервал повторения Т называется периодом, частота повторения f₀=1/T называется основной частотой.

К периодическим сигналам относят гармонические и полигармонические сигналы.

Непериодический сигнал – почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов, с произвольными частотами, отношение которых (хотя бы двух частот минимум ) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик.

Случайные сигналы представляют собой хаотические функции времени, значения которых в конкретный момент времени заранее неизвестны и не могут быть предсказаны с вероятностью, равной единице, например, речь или музыка, преобразованные в электрические процессы и т. д. К случайным сигналам относятся также шумы.

Детерминированные сигналы, в свою очередь, подразделяются на периодические, для которых выполняется условие S(t)=S(t+kT), где T – период, k – любое целое число, а под S(t) чаще всего понимаются изменяющиеся со временем ток, напряжение, иногда заряд. К непериодическим сигналам относится любой детерминированный сигнал, для которого выполняется условие S(t)=S(t+kT). Простейшим периодическим сигналом является, в частности, гармонический сигнал s(t) = A·cos(ω·t + φ).

Начертим временную диаграмму, то есть зависимость мгновенного значения электрической величины (u, i, e) от времени (t), в соответствии с исходными данными.

Определим частоту следования импульсов, которая будет равна частоте первой гармонике, по формуле:

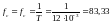, Гц.

Вычислим скважность, по формуле:

; .

При определении спектра необходимо рассчитать:

- постоянную составляющую по формуле:

, В; , В.

- амплитуды гармонических составляющих по формуле:

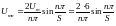, В,

где n – номер гармоники

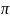– 3,14 в знаменателе и 180⁰ в аргументе sin ;

S – скважность.

Число рассчитываемых гармоник определяется n = 2 * S.

Но при этом мы видим, что амплитуда, номер которой равен или кратен S, обращается в ноль.

Результаты расчетов сведем в таблицу:

Сигнал	Umn , В
n	0	1	2	3	4	5	6
Первый	2	3,31	1,65	0,00	0,83	0,66	0,00
Второй	1,5	2,70	1,91	0,90	0,00	0,54	0,64

После чего строим временные и спектральные диаграммы для двух заданных сигналов. Под спектральной диаграммой понимают зависимость амплитуды гармонических колебаний от частоты (Um = f( )).

Пример временной диаграммы показан на рисунке 1

Рисунок 1 - Временная диаграмма сигналов

Расчёт спектральной диаграммы показан на рисунке 2.

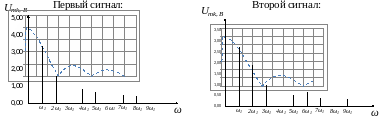
Рисунок 2 - Спектральные диаграммы сигналов

Состав спектра периодической последовательности прямоугольных импульсов зависит от величины отношения периода последовательности к длительности импульса, называемого скважностью импульсов.

За ширину спектра принимается диапазон частот, в пределах которого находится два первых лепестка. Ширина спектра определяется по формуле:

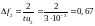кГц; кГц.