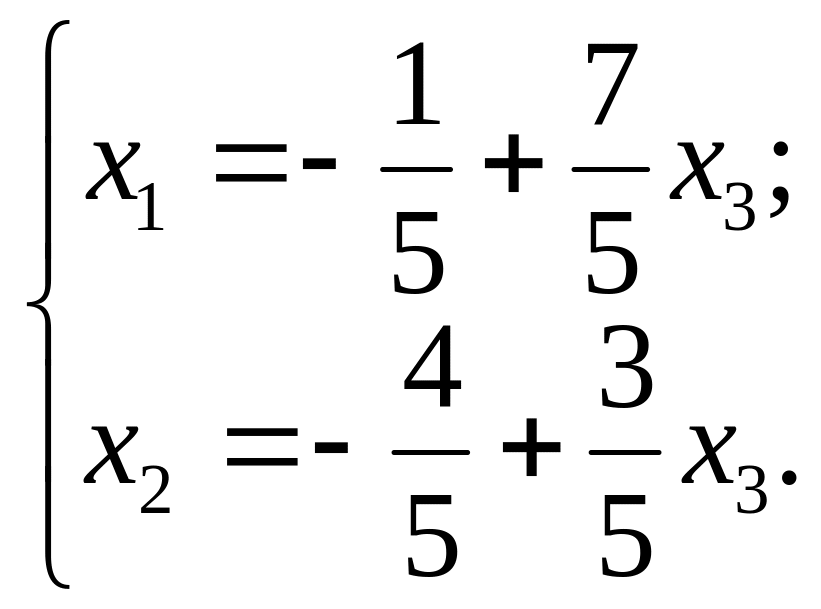- •Линейные методы оптимизации. Задачи линейного программирования
- •1.1 Общая постановка задачи линейного программирования.
- •Линейное программирование в экономике
- •1.3 Решение систем линейных алгебраических уравнений в форме жордановых таблиц
- •1.3.1 Основные понятия
- •1.3.2 Жордановы таблицы
- •1.3.3 Алгоритм решения слау в форме жордановых таблиц
- •1.3.4 Примеры решения типовых задач
- •1.3.5 Задания для самостоятельного решения
- •1.4 Базисные и опорные решения слау
- •1.4.1 Основные понятия
- •1.4.2 Алгоритм отыскания опорных решений слау
- •1.4.3 Примеры решения типовых задач
- •Задания для самостоятельной работы
- •Графическое решение задач линейного программирования
- •1.5.1 Геометрическая интерпретация
- •1.5.2 Алгоритм графического решения злп
- •1.5.3 Пример решения типовой задачи
- •1.5.4 Задания для самостоятельной работы
- •1.6 Симплексный метод решения задач линейного программирования
- •1.6.1 Укрупненный алгоритм симплексного метода
- •1.6.2 Алгоритм отыскания начального опорного плана
- •1.6.3 Алгоритм отыскания оптимального опорного плана
- •1.6.4 Пример решения типовой задачи
- •1.6.5 Задания для самостоятельной работы
- •Двойственность в линейном программировании
- •1.7.1 Понятие двойственности для симметричных задач
- •1.7.2 Экономическая интерпретация симметричных двойственных задач
- •1.7.3 Связь между решениями прямой и двойственной задачи
- •2. Оптимальное распределение ресурсов. Транспортная задача
- •2.1. Метод северо-западного угла (мсзу)
- •2.2. Метод минимального тарифа (ммт)
- •2.3. Определение оптимального плана перевозок методом потенциалов
- •2.4. Транспортная задача с усложнениями
- •2.5. Транспортная задача по критерию времени
- •2.6 Задания для самостоятельной работы
- •3. Элементы нелинейного программирования
- •Постановка задач нелинейного программирования
- •Особенности решения задач нелинейного программирования
- •Метод множителей Лагранжа
- •4 Метод наименьших квадратов
- •4.1 Некоторые типы эмпирических формул
- •Примеры решения типовых задач
- •4.3 Задания для работы в аудитории
- •4.4 Подбор эмпирических формул по выборочным данным
- •4.3 Задание для самостоятельной работы
- •Элементы сетевого планирования
- •При управлении такими проектами применяются специальные способы изображения сетей, позволяющие разработать очень эффективные и простые процедуры вычислений информации о состоянии проекта.
- •5.1 Построение сетевой модели
- •5.2 Наиболее ранний срок наступления события
- •5.3 Наиболее поздний срок наступления события
- •Пример 3. Для всех узлов (событий) сети из примера 1 определить наиболее поздний допустимый срок наступления события.
- •5.4 Резерв времени и критический путь
- •5.5 Оптимизация плана комплексных работ
- •5.6 Задания для самостоятельной работы
- •Литература
- •Методы решения оптимизационных задач
- •346493, Донской гау, пос. Персиановский,
1.3.3 Алгоритм решения слау в форме жордановых таблиц
Рассмотрим исходную СЛАУ в общей форме:
Запишем эту систему в виде нуль - равенств.

Внесем эту систему в жорданову таблицу:
-
1
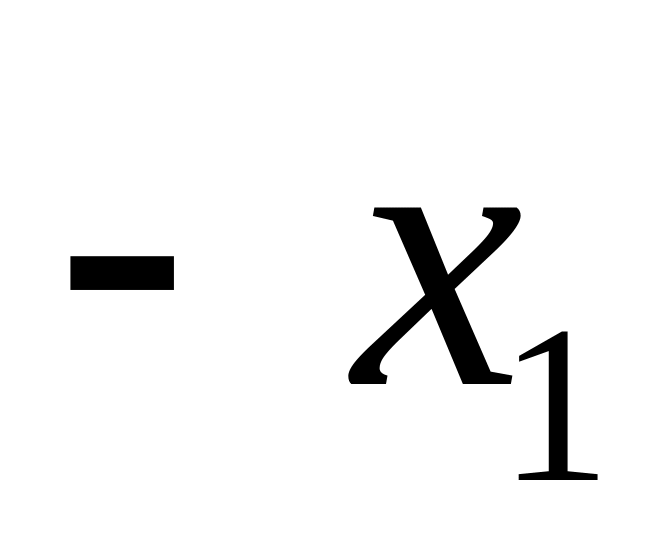 …
…
…
…

…
…
………………
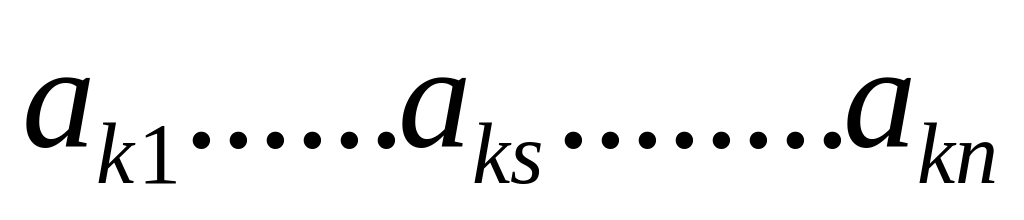
…
…
………………

Здесь на месте базисных переменных пока стоят нули.
Уравнения исходной системы записать в жорданову таблицу в виде нуль - равенств (нуль - строк).
Выполнить один шаг жордановых исключений.
Принять за разрешающую строку любое нуль-равенство, а за разрешающий столбец любой столбец ( ≠0).
В новой таблице поменять местами заглавные элементы разрешающей строки и разрешающего столбца (0 и
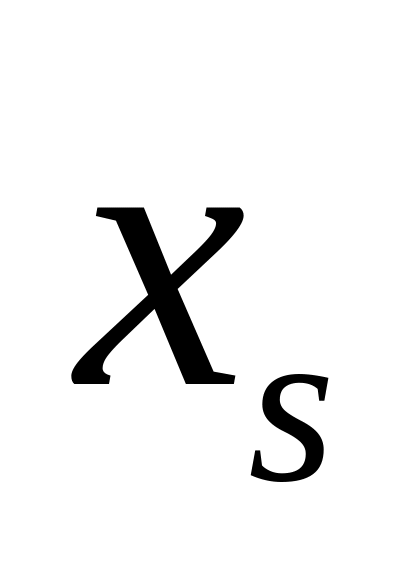 или
или
 и
и
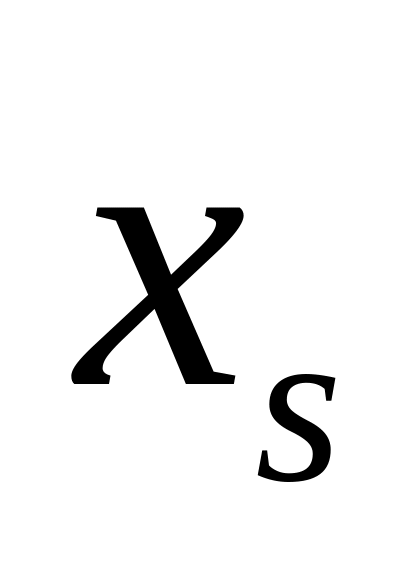 ).
).Выполнить пересчет таблицы. Правила пересчета приведены выше.
Вычеркнуть нуль-столбец (элементы разрешающегося столбца можно вообще не вычислять).
Проанализировать новую таблицу.
Если имеется нуль-строка со всеми нулевыми элементами, кроме свободного члена, то СЛАУ несовместна.
Если есть нуль-строки полностью состоящие из нулей, то их надо вычеркнуть.
Если нуль-равенства еще имеются, то необходимо вернуться на пункт II.
После ряда шагов жордановых исключений в таблице будет получено общее решение СЛАУ.
-
1
… …
…
…
………………
…
…
………………
Отметим, что если r= n, то в таблице останется только столбец свободных членов. В этом случае СЛАУ имеет единственное решение.
1.3.4 Примеры решения типовых задач
Пример 1. Решить СЛАУ.

Решение.
Составим жорданову таблицу.
|
1 |
|
|
15 |
2 -1 4 |
|
8 |
2 1 1 |
|
5 |
3 -1 0 |
Выберем разрешающий элемент. Он выделен жирным шрифтом и подчеркнут.
После пересчета элементов таблица принимает вид:
|
1 |
|
|
-17 |
-6 -5 -4 |
|
8 |
2 1 1 |
|
5 |
3 -1 0 |
Нуль - столбец можно вычеркнуть.
|
1 |
|
|
-17 |
-6 -5 |
|
8 |
2 1 |
|
5 |
3 -1 |
Выберем разрешающий элемент.
После пересчета элементов таблица принимает вид:
|
1 |
|
|
-42 |
-21 |
|
13 |
5 |
|
-5 |
-3 |
Разделим все элементы нуль - строки на -21.
|
1 |
|
|
2 |
1 |
|
13 |
5 |
|
-5 |
-3 |
Выберем разрешающий элемент.
После пересчета элементов таблица принимает вид:
|
1 |
|
2 |
|
3 |
|
1 |
Ответ: (2; 1; 3).
Пример 2. Решить СЛАУ.
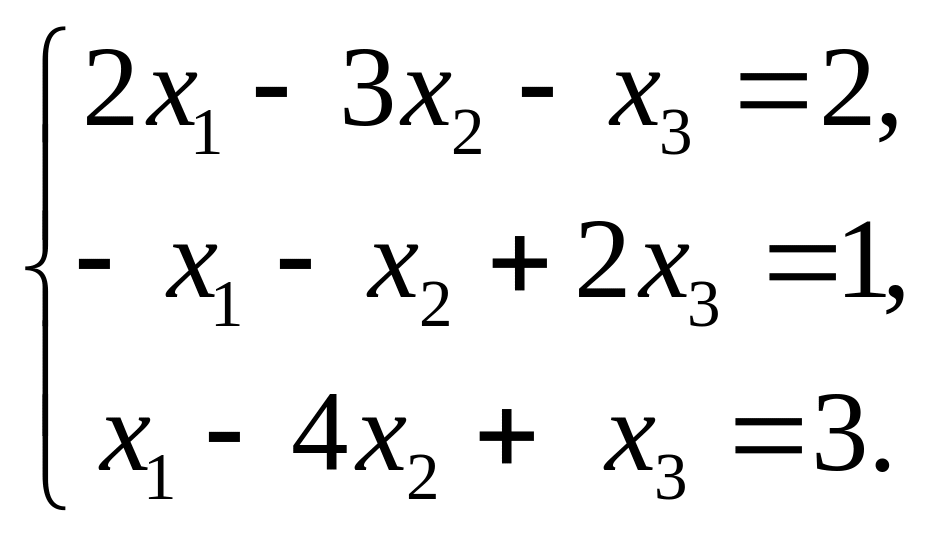
Решение.
Составим жорданову таблицу.
|
1 |
|
|
2 |
2 -3 -1 |
|
1 |
-1 -1 2 |
|
3 |
1 -4 1 |
Выберем разрешающий элемент.
После пересчета элементов таблица принимает вид:
|
1 |
|
|
-4 |
5 -3 |
|
4 |
-5 3 |
|
3 |
-4 1 |
Выберем разрешающий элемент.
После пересчета элементов таблица принимает вид:
|
1 |
|
|
-4/5 |
-3/5 |
|
0 |
0 |
|
-1/5 |
-7/5 |
Найдено общее решение СЛАУ в базисе (х1 ; х2):