1. Задача планирования

1. Экономическая постановка задачи

Предприятие выпускает несколько видов продукции, при этом расходуется несколько типов ресурсов. Известны запасы ресурсов каждого типа, даны нормы расхода каждого ресурса на единицу каждой продукции и доход от единицы каждой продукции. Определить план производства, обеспечивающий наибольший суммарный доход.

2. Математическая модель

2.1. Исходные параметры

– количество видов продукции

– количество типов ресурсов

– запасы ресурсов каждого вида

– нормы расхода i-го ресурса на единицу j-ой продукции

– доход от единицы j-ой продукции

2.2.Управляемые параметры

Пусть – объемы производства каждого вида продукции

– вектор управляемых параметров (решение, допустимое решение – план)

2.3.Формулировка критерия оптимальности

Сформулируем критерий оптимальности. Пусть целевая функция описывает суммарный доход на произвольном плане . Требуется найти его наибольшее значение

2.4. Ограничения модели

Чаще всего ограничения в экономических задачах отражают соотношения материального баланса (расход ресурса не может превосходить его запасов).

Пусть – расход i-го ресурса на произвольном плане . Система ограничений имеет вид:

Таким образом, задача объемного планирования ставится как задача определения такого набора управляемых параметров

,

на котором достигается наибольшее значение критерия

при условии

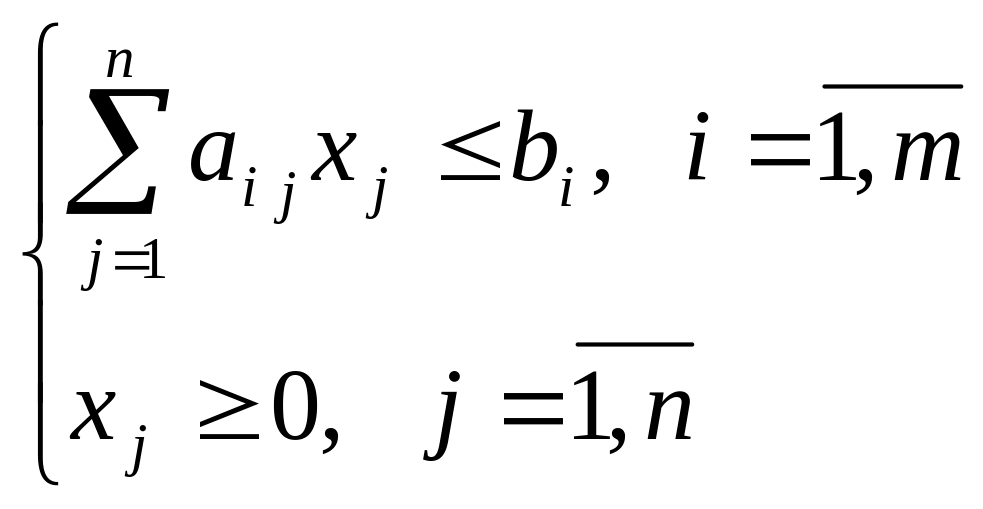
2. Задача о диете (рационе питания)

   1. Экономическая постановка задачи

Имеется несколько видов продуктов. Определить такой рацион питания (количество каждого вида продукта), чтобы были обеспечены нижние границы норм потребления некоторых питательных веществ, а стоимость рациона была наименьшая. Цены за единицу каждого продукта известны.

2. Математическая модель

2.1. Исходные параметры

– количество видов продукта

– количество контролируемых питательных веществ

– нормы потребления каждого питательного вещества (нижние границы)

– содержание i-го питательного вещества в единице j-го продукта

– цена каждого продукта

2.2. Управляемые параметры

– объем закупок каждого продукта

– вектор управляемых параметров (решение, план закупок или рацион)

2.3 Формулировка критерия оптимальности

Сформулируем критерий оптимальности. Пусть – стоимость произвольного рациона . Требуется найти рацион наименьшей стоимости

2.4. Ограничения модели

Потребление каждого питательного вещества не должно быть ниже нормы. Пусть – содержание i-го питательного вещества в произвольном рационе . Система ограничений имеет вид:

Таким образом, задача о диете ставится как задача определения такого набора управляемых параметров

,

на котором достигается наименьшее значение критерия

при условии

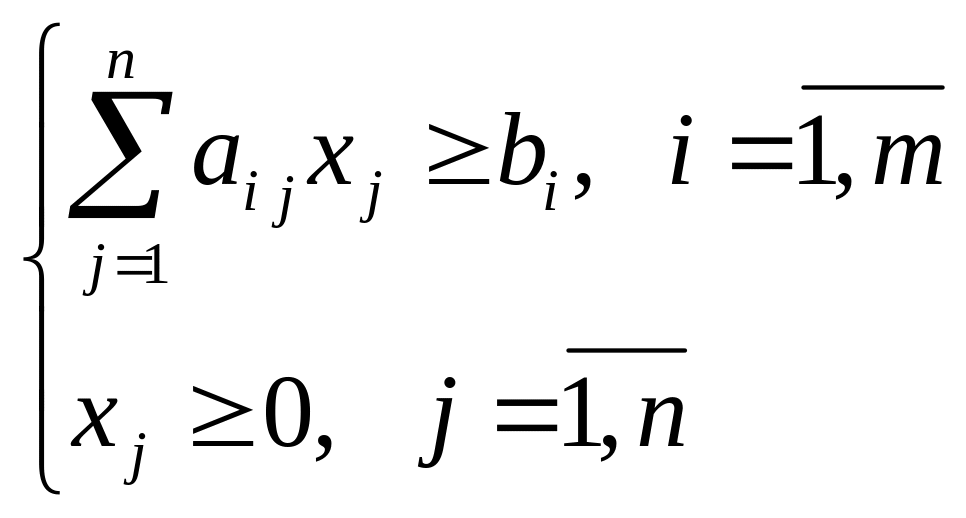
3. Транспортная задача.

   1. Экономическая постановка задачи

В некоторых пунктах A_i сосредоточен однородный товар в количестве соответственно а_i . Пункты B_j имеют потребность в этом товаре в количестве b_j соответственно. Известны тарифы перевозок единицы товара. Необходимо составить план перевозок, который обеспечит минимум транспортных затрат.