2. Задание на выполнение работы

1. Получить файл ранее полученного СЗМ изображения и произвести его анализ.

2. Выполнить фильтрацию изображения.

3. Измерить и сравнить параметры шероховатости изображений до и после фильтрации.

4. Построить Фурье-спектр изображения и измерить величины преобладающих пространственных частот спектра, сравнить соответствующие этим частотам периоды повторения элементов изображения с интервалами, полученными при измерениях на изображении.

Рис.3.1. Окно анализа изображений.

Выполнение анализа свойств поверхности изображения

3. Методические указания к выполнению работы

1. Ознакомиться с главой «Работа с полученными ранее файлами» Руководства пользователя.

2. Перейти к просмотру и обработке данных с помощью программы NOVA953.

2. Открыть файл, с которым будет проводиться работа, провести контрольное сечение изображения.

3. Определить характер имеющихся искажений и провести необходимую обработку и фильтрацию данных с помощью методов, доступных в программе.

4. Провести контрольные сечения файла после обработки и сравнить с сечением исходного изображения.

5. Вызвать окно Image Analysis (Рис.3.1.) при активном окне обработанного изображения. Изучить и описать гистограмму изображения. Зафиксировать значения величин средней и среднеквадратичной шероховатости.

- Открыть закладку Fourier Spectrum (Рис. 3.2., Рис. 3.3.). Определить по характеру спектра, имеются ли на изображении периодические структуры. Если имеются, то измерить величины преобладающих частот (переход в режим измерения частот осуществляется при нажатии кнопки Freq), указав на них на изображении Фурье-образа с помощью левой кнопки мыши. Сравнить периодичность изображений, измеренную при помощи инструмента расположенного над исходным изображением, с результатами, полученными с помощью Фурье-образа. Измерить величины углов между направлениями (инструмент ) по изображению Фурье-образа и сравнить с величинами углов между соответствующими сечениями исследуемого изображения.

Рис. 3.2. Окно анализа изображений. Выполнение анализа Фурье-спектра изображения

Рис. 3.3. Пример анализа изображения с помощью Фурье-спектра

4. Примерные контрольные вопросы и задания для допуска и сдачи работы

1. Какие типы искажений характерны для СЗМ изображений и по каким причинам они

возникают?

2. Каковы основные методы фильтрации СЗМ изображений?

3. Назовите некоторые методы определения количественных характеристик

изображений.

4. Для каких изображений следует воспользоваться частотным представлением?

5. Какую информацию об изображении можно получить по его Фурье-образу?

5. Литература

1. Дуда Р., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976, 511 стр.

2. Прэтт У. Цифровая обработка изображений – М.: Мир, 1982, книги 1, 2, 790 стр.

3. Ярославский Л.П. Введение в цифровую обработку изображений –

М.: Сов.радио, 1979. 312 стр.

5. Лабораторная работа №5 Исследование процесса субмикронной контактной фотолитографии

Цель работы

1. Ознакомиться с теоретическими основами субмикронной фотолитографии.

2. Овладеть навыками теоретической оценки некоторых режимов фотолитографии в УФ-диапазоне.

1. Теоретические основы фотолитографии

Известно, что вследствие волновой природы света изображение есть результат дифракции излучения на объекте [1, 2]. При экспонировании фоторезист регистрирует распределение интенсивности света на его поверхности, возникшее вследствие возмущения световой волны при ее прохождении через шаблон. С уменьшением размеров топологических фигур влияние дифракционных эффектов, связанных с волновой природой света, становится все более существенным.

Найдем распределение освещенности на слое фоторезиста с учетом дифракции. Будем считать, что на шаблон нормально к его поверхности падает плоская монохроматическая световая волна.

Любой фотошаблон можно характеризовать распределением прозрачности ε²(x^’, y^’), где x^’, y^’ – координаты в плоскости шаблона, фазой, которую приобретает световая волна при прохождении через шаблон, также зависящей от координат φ(x^’, y^’). Если маскирующий слой, нанесенный на шаблон полностью непрозрачен, то ε²(x^’, y^’) = 0 в тех областях шаблона, где этот слой имеется, и ε²(x^’, y^’) = ε²_с (ε²_с - прозрачность стеклянной пластины шаблона на участках свободных от маскирующего покрытия. Для так называемых транспарентных фотошаблонов прозрачность областей, имеющих маскирующее покрытие не равна нулю, а имеет конечную величину ε²_т.

Положим, что на наружной поверхности фотошаблона фаза φ(x^’, y^’)=0 (рис. 5.1). По мере прохождения монохроматической световой волны через толщу фотошаблона она приобретает фазу

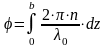(5.1),

где λ₀ – длина волны в вакууме, b – толщина фотошаблона, n – действительная часть показателя преломления.

Рис.5.1. Схема образования начального набега фазы.

Как толщина шаблона, так и показатель преломления в различных точках фотошаблона могут принимать различные значения, и поэтому фаза зависит от координат в плоскости фотошаблона x’и y’. Например, в транспарентных фотошаблонах толщина окрашенных областей обычно превосходит толщину светлых, т. е. имеется геометрический рельеф, приводящий к тому, что к плоскости b лучи 1 и 2 (рис.5.1) приходят с дополнительным набегом фазы.

Пусть на фотошаблон нормально к его поверхности падает плоская монохроматическая волна. Пусть на фотошаблоне имеется рисунок (рис.5.2), представляющий собой комбинацию прозрачных Г1 и темных Г2 участков. Предположим также, что на светлых участках поглощения волны не происходит, а темные области полностью поглощают излучение. Требуется определить освещенность в произвольной точке Р(x, y) на слое фоторезиста, отстоящем от фотошаблона на расстояние h. Данную задачу можно решить, воспользовавшись дифракционной формулой Кирхгофа [2]:

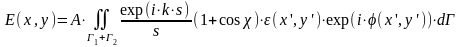(5.2),

где Е(x, y) – поле в точке (x, y) на поверхности фоторезиста, возбуждаемое участками волнового фронта Г1 и Г2; А – некоторая константа; k = 2·π/λ – волновое число; s – длина оптического пути от элемента волнового фронта dГ до точки наблюдения (x, y); χ – угол между нормалью к волновому фронту , проведенной из точки (x, y), и направлением из этой же точки на элемент dГ.

Рис. 5.2. Иллюстрация принципа суммирования световых волн на поверхности фоторезиста.

В случае транспарентных фотошаблонов формула (5.2) должна быть видоизменена. В этом случае так же, как в случае с непрозрачной маской, результирующее поле определяется суммой вкладов светлых участков изображения, однако к ним добавляется теперь сумма вкладов всех маскированных участков изображения. Очевидно, что в формуле (1.2) должен появиться член, содержащий множитель ε·exp(i·φ), учитывающий прозрачность маскирующего покрытия ε²т и начальный набег фазы φ.

Из рис. 5.2 видно, что длина оптического пути лучей

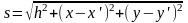, а косинусы углов их отклонения от нормали к поверхности волнового фронта .

Тогда на основании формулы Кирхгофа выражение для интенсивности света в точке P(x, y) можно записать в виде

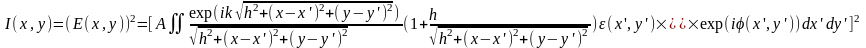
Если размеры элементов рисунка фотошаблона намного превосходят длину волны излучения, деленную на 2π, т. е. величины ε(x’, y’) и φ(x’, y’) мало меняются на длине λ/2π, то из-за быстрых осцилляций экспоненциального множителя в (1.2) существенный вклад в интеграл вносят области интегрирования (x-x’) и (y-y’) << h. Поэтому корни в предыдущей формуле можно разложить в ряд по (x-x’)²/h² и (y-y’)²/h². В результате получим:

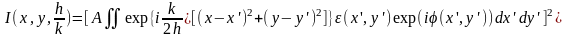(5.3)

С помощью выражения 5.3 легко проследить, как ведет себя функция интенсивности при стремлении зазора h к нулю. Видно, что экспоненциальный фактор осциллирует с изменением (x-x’) и (y-y’), причем характерный масштаб осцилляций 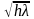. Если зазор стремится к нулю, то осцилляции становятся настолько быстрыми, что в фигурирующих под знаком интеграла функциях можно положить x=x’ и y=y’. Тогда функция распределения интенсивности будет пропорциональна прозрачности фотошаблона, т. е. рисунок с шаблона на фоторезист переносится идеально. Если же зазор на равен нулю, то вследствие волновых свойств света распределение интенсивности на фоторезисте не совпадает с распределением прозрачности на фотошаблоне, т. е. перенесенный рисунок искажается дифракционными эффектами.

Характерный масштаб искажений, так же, как и масштаб осцилляций интенсивности, составляет величину порядка , которая характеризует размер зоны Френеля.

Если маскирующие участки фотошаблона характеризуются прозрачностью ε²_т и фазой φ_т, а соответствующие величины для светлых участков - ε²_с и φ_т, то в выражении 5.3 можно заменить двойной интеграл суммой интегралов по светлой и темной областям. Кроме того, если в качестве общего множителя вынести величину ε_с•exp(i φ_c), тогда можно записать:

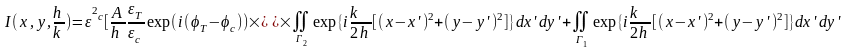(5.5)

Из (1.5) видно, что зависимость интенсивности света на фоторезисте от координат x и y определяется разностью фаз φ_т – φ_с = φ и отношением прозрачности темных и светлых участков ε²_Т/ ε²_с = ε², т. е. приведенной прозрачностью. Отношение прозрачности светлого участка к прозрачности маски называют контрастом:

К = ε²_с/ ε²_Т (5.6)

Если маскирующие участки полностью непрозрачны, т. е. ε²_Т = 0, то имеется случай бесконечного контраста. В этом случае первое слагаемое в выражении (1.5) исчезнет, и распределение интенсивности перестанет зависеть от фаз.

Если характерный размер топологического элемента обозначить 2а, то в зависимости от соотношения 2а и принято различать дифракцию Френеля ( <<2а) и Фраунгофера ( >>2а). Фраунгоферовская дифракция намного легче для анализа и рассматривается применительно к фотолитографии достаточно подробно, например в [3]. Анализ дифракции Френеля, а тем более промежуточных случаев ( ~2а), более сложен. Однако в практической контактной фотолитографии реализуются, как правило, именно френелевская, либо промежуточная дифракционные ситуации.

Распределение интенсивности в картине дифракции Френеля на непрозрачной полуплоскости можно найти в большинстве курсов физической оптики [4, 5]. Решение задачи о распределении интенсивности в случае транспарентной полуплоскости встречается значительно реже [6]. Однако мы более подробно рассмотрим дифракцию на полосках конечной ширины. Именно такая проблема наиболее часто возникает на практике, например, при моделировании процесса формирования области затвора МОП транзистора с длиной канала менее 1 мкм.

Наиболее часто в реальных топологических изображениях встречается простейший элемент – одиночная полоска. Это может быть темная маскирующая полоска на светлом поле или, светлая - на темном поле.

Рассмотрим дифракционную картину, порожденную одной бесконечной маскирующей полоской шириной 2а с приведенной прозрачностью ε² = ε²_Т/ ε²_с, расположенной параллельно экрану на расстоянии h от него (рис. 5.3).

Рис. 5.3. Схема для расчета дифракционного распределения интенсивности под маскирующей полоской.

За начало координат (x=0) принимают проекцию середины полоски на экран. Тогда дифракционная картина будет симметрична относительно линии x=0, и можно ограничиться рассмотрением ее половины, т. е. интервала от x=0 до x=∞. Кроме того, распределение интенсивности в этом случае не зависит от координаты y, и задача становится одномерной. В этом случае для распределения интенсивности можно записать:

(5.7)

Проведем замену переменной

, введем безразмерную координату 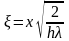и безразмерную полуширину полоски 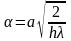. Тогда второй интеграл в (1.7) можно записать:

Исключим из рассмотрения константу перед интегралом и вычислим оставшееся выражение, предварительно разбив его на два интеграла по пределам интегрирования:

Первый интеграл равен:

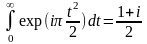
Второй интеграл выражается через интегралы Френеля:

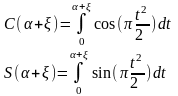
Аналогичным образом можно вычислить все остальные интегралы.

Введем обозначения

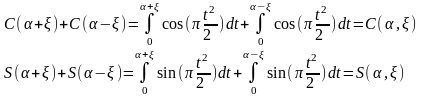
С учетом того, что константа равна I₀/2 выражение для интенсивности примет вид:

(5.8)

Для прозрачной полоски на маскирующем поле распределение интенсивности на фоторезисте можно рассчитать по этой же формуле, учитывая лишь, что прозрачность светлой полоски ε²_с = 1/ε², и в постоянный множитель перед I(α,ζ) войдет также величина 1/ε².

Характеристические точки кривой дифракционного распределения интенсивности

Очевидно, что для фотошаблона с ε² = 0 (полностью непрозрачная маска, например, фотошаблон с маскирующим покрытием на основе металлической пленки, скажем хрома) величина набега фазы φ не имеет физического смысла (φ=0). Поэтому для шаблонов такого типа может варьироваться только ширина полоски и зазор между шаблоном и фоторезистом. Кроме того, фотошаблон с ε² = 1 и φ=0 представляет собой прозрачную пластину без геометрического рельефа и не представляет интереса для рассмотрения.

Вид конкретного дифракционного распределения интенсивности приведен на рис. 5.4. На рисунке представлена правая часть распределения интенсивности при дифракции света на одиночной маскирующей полоске (напомним, что дифракционная картина симметрична относительно проекции центра маскирующей полоски). По оси ординат отложено значение отношения интенсивностей света I(ξ)/I₀ на поверхности фоторезиста в относительных единицах (при умножении на 100 мы получим интенсивность в %). По оси x приводится значение безразмерной координаты ξ. Граница геометрической тени соответствует координате ξ=0 (точка С на графике). Маскирующая полоска расположена в области отрицательных значений безразмерной координаты (влево от точки С). В области положительных значений ξ располагается светлая область фотошаблона, не замаскированная полоской.

Рис 5.4. Дифракционное распределение интенсивности.

Как видно из рисунка, распределение интенсивности носит достаточно сложный характер, и имеет следующие особенности.

1. В некоторых областях геометрической тени (область фоторезиста замаскированная элементом) интенсивность отлична от нуля. В этой области вблизи от края полоски располагается дифракционный максимум распределения (точка А на графике), в котором значение интенсивности имеет определенную величину (I=0,25 для данного примера) значительно отличающую от нуля.

2. В незамаскированной области фоторезиста распределение интенсивности также не постоянно. В этой области располагается дифракционный минимум (точка В на графике), в котором значение интенсивности может быть существенно меньше 1 (I=0,8 для данного примера).

3. Важным параметром при формировании изображения на фоторезисте является также значение интенсивности в точке соответствующей границе полоски (точка С на графике, I=0,2 для данного примера).

Наличие осцилляций на кривых распределения интенсивности приводит к тому, что при не правильно выбранном времени экспонирования или режиме проявления могут возникать характерные дефекты резистивной маски.

Например, при завышенном времени экспонирования экспозиция а точке А может оказаться достаточной для полного удаления фоторезиста в этой точке при проявлении. В этом случае в области тени, где требуется сохранить маскирующую пленку фоторезиста, появятся сквозные полосы обнаженной подложки, ориентированные вдоль края полоски, т. е. повторные контуры изображения или так называемый «двойной край». При заниженном времени экспонирования экспозиция в точке В может оказаться недостаточной для полного удаления фоторезиста и в освещенной области изображения вдоль края элемента сохранятся валики неудаленного при проявлении фоторезиста, т. е. образуется двойной край в элемента светлой области.

Очевидно, что разность интенсивностей главного дифракционного максимума в тени (точка А) и минимально освещенной точки светлого поля (точка В) определяет некоторый характерный интервал ΔI_р, обеспечивающий формирование изображение на слое фоторезиста без двойного края в области света и тени. С уменьшением рабочего интервала необходимо экспонировать фоторезист со все более жесткими допусками на экспозицию (допусками по времени облучения). При этом всякие случайные факторы (неоднородность освещенности рабочего поля, флуктуации яркости источника, неточность времени экспонирования и др.) все в большей мере будут снижать воспроизводимость Фотолитографического процесса и увеличивать вероятность появления брака.

Важной особенностью дифракционного распределения интенсивности оказывается размытие границ топологических элементов, приводящее к тому, что размеры реализованных элементов оказываются зависящими от экспозиции. Наклон переходной области между светлыми и темными участками изображения (краевой градиент в точке С на графике) определяет удельный уход размера на единичную ошибку экспонирования Δα_уд=Δ ξ/ ΔI.

Пусть заданы тип фоторезиста, его толщина и стабилизированы условия проявления (задан состав проявителя, время проявления, температура проявителя, объем проявителя и т. д.) Тогда темп удаления и толщина удаленного в процессе проявления слоя фоторезиста будут зависеть только от экспозиции. В этих условиях минимальная экспозиция, достаточная для полного удаления этого слоя фоторезиста в данных условиях проявления будет пороговой экспозицией Н_пор.

Предположим, что нам известна величина пороговой экспозиции в данных условиях проведения фотолитографического процесса. Обозначим I₀ интенсивность в светлых участках вдали от края геометрической тени, принятую за 100%, и t₀ – время экспонирования участков фоточувствительного слоя, освещаемых световым потоком интенсивности I₀, соответствующее Н_пор. Тогда время экспонирования t_э, необходимое для того, чтобы участки, освещаемые потоком с интенсивностью I(ξ), набрали суммарную экспозицию, равную Н_пор, определяется из соотношения:

t_э =(I₀/ I(ξ))*t₀

Знание распределения I(ξ) для заданного топологического элемента и t₀ из предварительного эксперимента дает все необходимые количественные данные для расчета условий формирования изображений на слое фоторезиста. В качестве примера воспользуемся распределением интенсивности приведенном на рис. 5.4.

Для точной передачи размера элемента необходимо, чтобы за время экспонирования t_э все участки на фоторезисте, подлежащие удалению при проявлении, накопили экспозицию Н>Н_пор и, наоборот, участки, на которых фоторезист должен быть сохранен, Н<Н_пор. Очевидно, что такая ситуация реализуется, когда интенсивность под краем геометрической тени I_к (точка С на графике) за время t_э обеспечит экспозицию

Н = (I₀/I_к)*t₀ = Н_опт

Будем эту экспозицию называть оптимальной. Из рис. 5.4 определяем, что I_к = 0,2 (20%). Тогда необходимое время экспонирования для точной передачи размера элемента

t_э = (I₀/I_к)*t₀ = (1/0,2)* t₀ = 5* t₀

Из этого же распределения можно найти максимальное время экспонирования t_эв, превышение которого приведет к образованию двойного края в области геометрической тени:

t_эв = (I₀/I_А)*t₀ = (1/0,25) *t₀ = 4*t₀

Точно также минимальное время экспонирования, занижение которого ведет к появлению двойного края в светлых областях:

t_эн = (I₀/I_В)*t₀ = (1/0,8) *t₀ = 1,25*t₀

Таким образом, мы можем оценить границы интервала Δt_э, экспонирование внутри которого не приводит к появлению дефекта в виде двойного края. Из определения пороговой экспозиции ясно, что при налаженной методике ее измерения на основании рассчитанных распределений освещенности на поверхности фоторезиста можно судить о геометрических размерах и форме вскрытых окон в сформированной резистивной маске.