5. Вычисление расчетных значений параметров оптимизации
Определим расчетные значения параметров оптимизации путем подстановки соответствующих знаков (+ или −) в выражение (3.6). Тогда получим следующие расчетные значения:
6. Определение критерия фишера и проверка модели на адекватность
6.1. Вычисление критерия Фишера
Адекватность модели в целом будем определять по критерию Фишера. Экспериментальное значение F-критерия (критерия Фишера) равно:
,
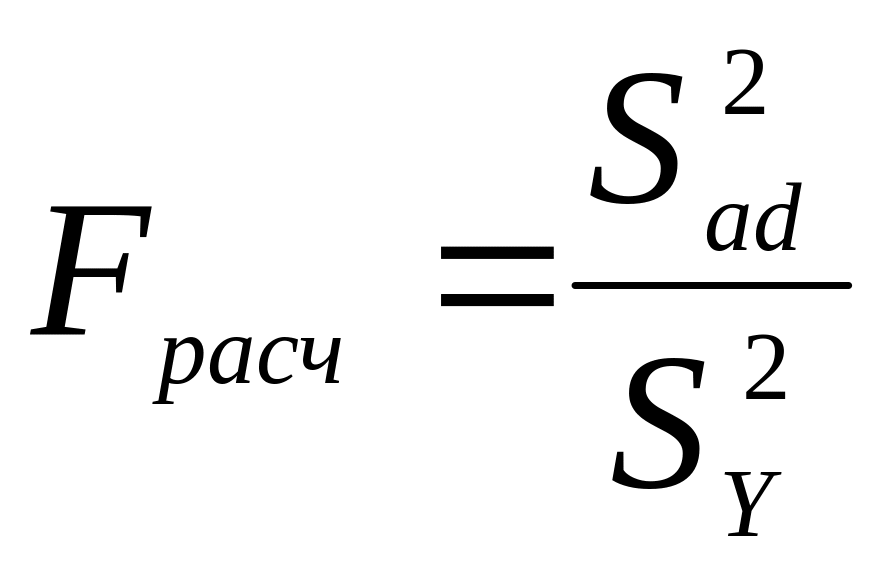(6.1)
где
− дисперсия адекватности модели
(остаточная дисперсия),
− дисперсия опыта (эксперимента).
Вычислим дисперсию адекватности по формуле:
,
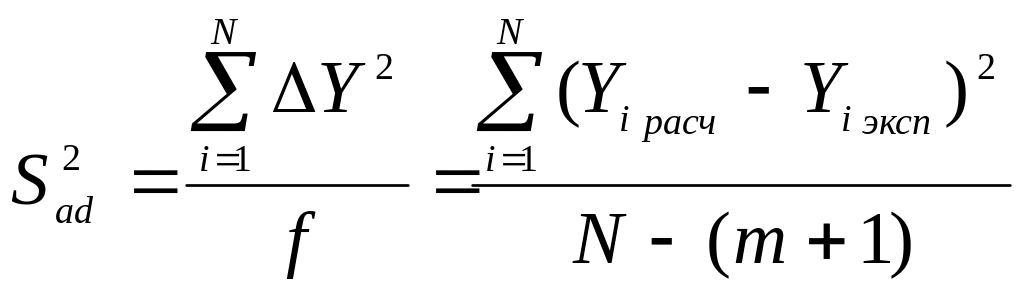(6.2)
где f − число степеней свободы, m − количество значимых коэффициентов модели (в уравнении регрессии, кроме ), N − количество опытов.
Сначала вычислим разницу между расчетными и экспериментальными значениями параметров оптимизации и заполним таблицу 2:
(6.3)
Также найдем (∆Y)2 и заполним таблицу 2.
Подставляя известные значения в выражение (6.2), вычислим дисперсию адекватности модели:
Экспериментальное значение F-критерия (критерия Фишера) вычислим по (6.1).
Табличное
значение критерия Фишера (
)
определяется по таблице. Значение
F-критерия
для уровня значимости
зависит от
(число степеней свободы большей
дисперсии),
(число степеней свободы меньшей
дисперсии). Учитывая уровень значимости
и зная степень свободы, табличное
значение критерия Фишера равно
.
6.2. Проверка модели на адекватность
Полученную
с помощью факторного планированного
эксперимента модель объекта необходимо
проверить на адекватность. Проверяется
адекватность модели, то есть пригодность
полученной модели для описания реального
объекта исследования, по отношению
дисперсий адекватности и параметра
оптимизации
.
Сравним
расчетные и табличные значения критериев
Фишера и сформулируем вывод об адекватности
модели. Согласно условию
− модель неадекватна и соответственно
при
− адекватна.
Таким образом, в нашем случае:
;
.
,
что говорит об адекватности модели.
Вывод:
Уравнение регрессии для данного полного факторного эксперимента выглядит следующим образом:
.
Так как , модель адекватна, то есть пригодна для описания реального объекта исследования.
Наибольшее
влияние на результат шлифования оказывает
скорость движения стола шлифовального
станка (
),
наименьшее же − твердость абразивного
инструмента (
).
Влияние такого фактора, как глубина
шлифования, также существенно (
).
Приложение
Таблица 1 – Варианты задания
№ |
Варианты значений, Yэксп |
|||||||||
опыта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
0,83 |
0,81 |
0,81 |
0,85 |
0,79 |
0,84 |
0,78 |
0,79 |
0,83 |
0,82 |
2 |
0,66 |
0,63 |
0,66 |
0,73 |
0,6 |
0,67 |
0,6 |
0,61 |
0,65 |
0,63 |
3 |
0,91 |
0,99 |
0,84 |
0,99 |
0,9 |
0,91 |
0,92 |
0,92 |
0,97 |
0,96 |
4 |
0,83 |
0,9 |
0,98 |
0,84 |
0,87 |
0,86 |
0,84 |
0,85 |
0,88 |
0,9 |
5 |
1 |
0,94 |
0,73 |
0,94 |
0,95 |
1 |
0,98 |
0,97 |
0,96 |
1 |
6 |
0,71 |
0,8 |
0,92 |
0,8 |
0,75 |
0,75 |
0,73 |
0,74 |
0,81 |
0,79 |
7 |
1 |
0,95 |
0,85 |
1 |
0,94 |
0,96 |
0,98 |
0,95 |
1 |
0,99 |
8 |
1 |
0,97 |
1 |
0,98 |
0,97 |
1 |
0,99 |
0,97 |
0,98 |
0,99 |
№ |
Варианты значений, Yэксп |
|||||||||
опыта |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
1 |
0,95 |
1 |
0,98 |
0,97 |
0,96 |
1 |
0,8 |
0,73 |
0,8 |
0,75 |
2 |
0,75 |
0,75 |
0,73 |
0,74 |
0,81 |
0,79 |
0,95 |
0,96 |
1 |
0,94 |
3 |
0,91 |
0,99 |
0,98 |
0,99 |
0,9 |
0,91 |
0,92 |
0,92 |
0,97 |
0,96 |
4 |
0,85 |
0,84 |
0,87 |
0,86 |
0,84 |
0,85 |
0,88 |
0,99 |
0,98 |
0,99 |
5 |
0,95 |
0,94 |
0,95 |
1 |
0,98 |
0,97 |
0,96 |
0,9 |
0,85 |
0,84 |
6 |
0,73 |
0,8 |
0,75 |
0,75 |
0,73 |
0,74 |
0,81 |
0,94 |
0,95 |
0,94 |
7 |
0,99 |
0,9 |
0,91 |
0,92 |
0,92 |
0,97 |
0,63 |
0,66 |
0,73 |
0,6 |
8 |
0,84 |
0,87 |
0,86 |
0,84 |
0,85 |
0,88 |
0,99 |
0,98 |
0,99 |
0,9 |
№ |
Варианты значений, Yэксп |
|||||||||
опыта |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
1 |
0,84 |
0,87 |
0,86 |
0,84 |
0,85 |
0,88 |
0,99 |
0,75 |
0,73 |
0,74 |
2 |
0,94 |
0,95 |
1 |
0,98 |
0,97 |
0,96 |
0,9 |
0,92 |
0,92 |
0,97 |
3 |
0,98 |
0,99 |
0,9 |
0,91 |
0,92 |
0,84 |
0,87 |
0,86 |
0,84 |
0,85 |
4 |
0,87 |
0,86 |
0,84 |
0,85 |
0,88 |
0,94 |
0,95 |
1 |
0,98 |
0,97 |
5 |
0,74 |
0,81 |
0,79 |
0,95 |
0,96 |
0,8 |
0,75 |
0,75 |
0,73 |
0,74 |
6 |
0,99 |
0,9 |
0,91 |
0,92 |
0,92 |
0,75 |
0,75 |
0,75 |
0,73 |
0,74 |
7 |
0,86 |
0,84 |
0,85 |
0,88 |
0,99 |
0,96 |
0,91 |
0,92 |
0,92 |
0,97 |
8 |
1 |
0,98 |
0,97 |
0,96 |
0,9 |
1 |
0,86 |
0,84 |
0,85 |
0,88 |