
- •Математические основы теории автоматического управления
- •Цели и задачи курсовой работы
- •Содержание.
- •Список литературы.
- •Пример решения
- •Описание пассивного четырёхполюсника при помощи дифференциального уравнения.
- •Получение передаточной функции пассивного четырёхполюсника по каналу «Вход» - «Выход» и нахождение величины выходного напряжения.
- •Получение частотных характеристик.
- •Получение передаточной функции в терминах пространства состояний
- •Получение передаточной функции пассивного четырёхполюсника в дискретной форме
- •Институт металлургии и химической технологии им. С. Б. Леонова Кафедра автоматизации производственных процессов
Получение частотных характеристик.
Частотные
характеристики могут быть получены из
передаточной функции
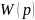 путем замены комплексной переменной
путем замены комплексной переменной
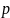 на
на
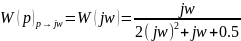
Воспользовавшись
выражением
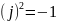 ,
а так же правилом деления двух комплексных
чисел преобразуем получившееся выражение
и выделим действительную и мнимую части
,
а так же правилом деления двух комплексных
чисел преобразуем получившееся выражение
и выделим действительную и мнимую части
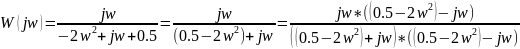 =
=
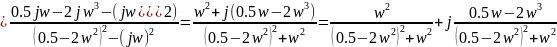
Таким
образом мы получили функцию
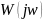 , которая представляет собой
амплитудно-фазовуя частотную характеристику (АФЧХ).
, которая представляет собой
амплитудно-фазовуя частотную характеристику (АФЧХ).
Далее выделяем из неё действительную частотную характеристику ДЧХ:
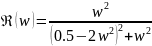
и мнимую частотную харакеристику (МЧХ)
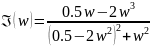


По известным ДЧХ и МЧХ находим амплитудно-частотную характеристику АЧХ и фазо-частотную характеристику (ФЧХ)
Амплитудно-частотная характеристика (АЧХ) — зависимость амплитуды выходного сигнала от частоты входного гармонического сигнала
Фазочастотная характеристика (ФЧХ) — зависимость разности фаз между выходным и входным сигналами от частоты сигнала, функция, выражающая (описывающая) эту зависимость, также — график этой функции.
АЧХ:


ФЧХ:




Далее построим логарифмическую амплитудно-фазовую частотную характеристику (ЛАФЧХ, в иностранной литературе часто называют диаграммой Боде)- представление частотного отклика линейной стационарной системы в логарифмическом масштабе.
ЛАФЧХ строится в виде двух графиков: логарифмической амплитудно-частотной характеристики(ЛАЧХ) и логарифмической фазо-частотной характеристики(ЛФЧХ), которые обычно располагают друг под другом.
ЛАЧХ — это зависимость модуля коэффициента усиления устройства, от частоты в логарифмическом масштабе.
По оси абсцисс откладывается частота в логарифмическом масштабе, единица измерения — безразмерная величина
По оси ординат откладывается амплитуда выходного сигнала в логарифмических безразмерных величинах: A_log(w)
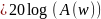
ЛФЧХ — это зависимость фазы выходного сигнала от частоты в полулогарифмическом масштабе:
по оси абсцисс откладывается частота в логарифмическом масштабе
по оси ординат откладывается выходная фаза в угловых градусах или радианах.

Получение передаточной функции в терминах пространства состояний
Пространство состояний — в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение её состояний.
В пространстве состояний создаётся модель динамической системы, включающая набор переменных входа, выхода и состояния, связанных между собой дифференциальными уравнениями первого порядка, которые записываются в матричной форме. В отличие от описания в виде передаточной функции и других методов частотной области, пространство состояний позволяет работать не только с линейными системами и нулевыми начальными условиями.
Для
случая линейной системы c
входами, {\displaystyle
q}  выходами и {\displaystyle
n}
выходами и {\displaystyle
n}  переменными состояния описание имеет
вид:
переменными состояния описание имеет
вид:
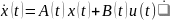 {\displaystyle
{\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}
{\displaystyle
{\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}
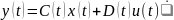 {\displaystyle
{\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}
{\displaystyle
{\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}
{\displaystyle \mathbf {y} (t)=C(t)\mathbf {x} (t)+D(t)\mathbf {u} (t)}
Где
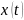 {\displaystyle
x(\cdot )} — вектор
состояния,
элементы которого называются состояниями
системы
{\displaystyle
x(\cdot )} — вектор
состояния,
элементы которого называются состояниями
системы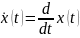
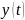 {\displaystyle
y(\cdot )} — вектор
выхода,
{\displaystyle
y(\cdot )} — вектор
выхода,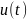 {\displaystyle
u(\cdot )} — вектор
управления,
{\displaystyle
u(\cdot )} — вектор
управления,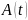 {\displaystyle
A(\cdot )} — матрица
системы,
{\displaystyle
A(\cdot )} — матрица
системы,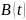 {\displaystyle
B(\cdot )} — матрица
управления,
{\displaystyle
B(\cdot )} — матрица
управления,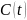 {\displaystyle
C(\cdot )} — матрица
выхода,
{\displaystyle
C(\cdot )} — матрица
выхода, {\displaystyle
D(\cdot )} — матрица
прямой связи.
{\displaystyle
D(\cdot )} — матрица
прямой связи.
Размерности матриц и векторов
- матрица
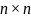
- матрица
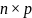
- матрица
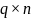
- матрица

Таким образом, для нашей цепи необходимо составить систему дифференциальных уравнений первого порядка, которые описывали бы её.
В
данной цепи изменение двух параметров
описывается дифференциальными
уравнениями: это ток
 протекающий через индуктивность
протекающий через индуктивность
 и напряжение
и напряжение
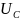 на конденсаторе
на конденсаторе
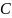 .
Эти два параметра и примем за параметры
системы
.
.
Эти два параметра и примем за параметры
системы
.
Используя закономерности электротехники, применяемые ранее для данной цепи запишем.
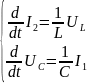
При этом
Сделаем следующие замены
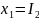
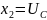
Система примет следующий вид

Далее
выразим
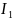 через параметры цепи
через параметры цепи
По 1-му закону Кирхгофа
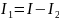
По закону Ома
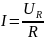
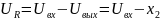
Подставляем в ()
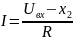
Получаем
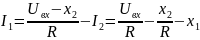
Подставляем выражение для в систему уравнений

Составим уравнение описывающее выход объекта:
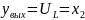
Таким образом, система уравнений, описывающая данную цепочку в терминах пространства состояний, будет иметь следующий вид с учетом нулевых коэффициентов:
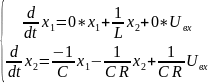
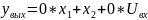
Далее по данной системе уравнений составляем матрицы
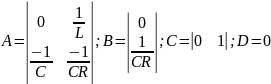
Для
проверки воспользуемся формулой перехода
от записи в пространстве состояния к
передаточной функции, предварительно
подставив значение параметров
 :
:
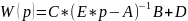
Где,
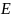 – единичная матрица , совпадающая по
размеру с матрицей A,
– комплексная переменная,
– единичная матрица , совпадающая по
размеру с матрицей A,
– комплексная переменная,
 – матрицы описания объекта в пространстве
состояния
– матрицы описания объекта в пространстве
состояния
В результате получаем такую же передаточную функцию как в разделе 2
Получить запись в пространстве состояния можно и другим способом. Сейчас мы получили запись в пространстве состояний основываясь на известных уравнениях электротехники, изначально строя запись в соответствии с стандартной записью
{\displaystyle {\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}
{\displaystyle {\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}
Так же запись в пространстве состояний можно получить, если уже имеем дифференциальное уравнение, которое описывает наш объект. В данном случае у нас данное уравнение получено в разделе 1.
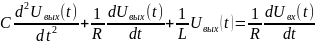
Далее рассмотрим общую методику на случай линейной системы с постоянными параметрами одним входом и одним выходом описываемой уравнением
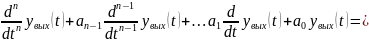
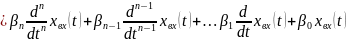
Данное уравнение приведено к виду что бы коэффициент перед старшей производной в левой части был равен 1 .
Далее в сокращенной форме представим получение записи в пространстве состояний. Более подробное объяснение можно получить в соответствующей литературе.
Путем замен понижаем порядок данного дифференциального уравнения, получая при этом систему дифференциальных уравнений первого порядка.
Делаем следующие замены
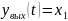 ,
,
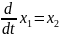 ,
,
 …
…
Из
первоначального дифференциального
уравнения выражаем производную высшего
порядка, относящуюся к выходной переменной
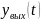
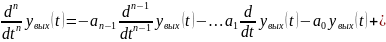
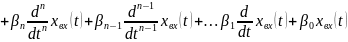
На основании произведенных замен составляем систему дифференциальных уравнений первого порядка
………….

Из
данной системы дифференциальных
уравнений получим матрицу A,
состоящую из коэффициентов перед
неизвестными
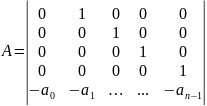
Далее
необходимо найти коэффициенты
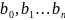 ,
которые вычисляются по следующим
формулам
,
которые вычисляются по следующим
формулам
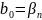


……………………………….
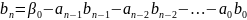
Из этих коэффициентов формируем вектор B

Уравнение выхода
{\displaystyle {\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}
в нашем случае запишется следующим образом

Таким
образом, вектор
 ,
а вектор C
запишется в следующем виде
,
а вектор C
запишется в следующем виде
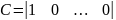
Количество элементов в векторе С равно n
Получим запись в пространстве состояний для нашего объекта
Делаем следующие замены
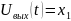 ,
,
Выражаем из нашего уравнения вторую производную, делаем соответствующие замены и записываем систему дифференциальных уравнений первого порядка
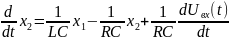
Уравнение выхода
Получаем матрицу A

Вектор C
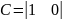
Произведем
расчёт коэффициентов
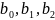
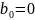
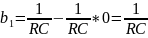
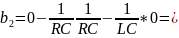
Таким образом, вектор B запишется как
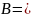
Вектор
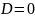
Так же сделаем проверку и воспользуемся формулой перехода от записи в пространстве состояния к передаточной функции, предварительно подставив значение параметров :
В результате снова получаем такую же передаточную функцию как в разделе 2
Стоит отметить, что разными способами мы получили разные записи в пространстве состояний, при этом передаточная функция получается одинаковой в обоих случаях. Одной передаточной функции может соответствовать множество записей в пространстве состоянии, но записи в пространстве состояний соответствует единственная передаточная функция.
