2.1.2.Отражение и преломление света тонкими слоями.

Параметрами образца со слоем (рис.2.1.,a), измеряемыми оптическими способами или влияющими на результат измерения являются:

- n₁-показатель преломления окружающей среды;

- n₂= n₂-ik₂ - комплексный показатель преломления слоя;

- n₃=n₃-ik₃ - комплексный показатель преломления подложки;

- h₂ и h₃ -_{_}толщина слоя и подложки;

Величины n и k представляют показатель преломления и главный показатель поглощения соответственно и называются оптическими постоянными или оптическими характеристикми среды.

Показатель поглощения , причем 4,34[см^-1]=-10lgT,

где Т - коэффициент пропускания.

Параметрами, определяющими конструкцию покрытия, являются:

- оптические толщины слоев nh;

- показатели преломления слоев n_m и n_m+1 и т.д. ;

- число слоев m.

В общем случае оптические толщины выражаются в долях от некоторой длины волны , находящейся в заданном участке спектра ₁- ₂ (рис.2.1, в).

Рис.2.1., в. Спектральные кривые отражения трехслойных систем.

К основным параметрам, характеризующим эффективность покрытия, относятся:

- остаточное отражение _ост;

- ширина зоны просветления, ограниченная длинами ₁ и ₂, отражение для которых составляет 0,5% или 1%.

Для удобства сопоставления покрытий, снимающих отражение в различных участках спектра, ширина зоны просветления может быть представлена в виде отношений:

₂/₁ или _0,5=

Информация о параметрах покрытия при оптических измерениях содержится в характеристиках световой волны, прошедшей через покрытие, или отраженной от него. Основными измеряемыми характеристиками световой волны являются интенсивность, скачок фазы, форма волнового фронта, состояние поляризации, спектр и направление распространения. В основе большинства оптических способов измерения параметров слоев лежит использование энергетических коэффициентов отражения R и пропускания T слоя, нанесенного на подложку.

Формулы для R и T получаются с учетом многолучевой интерференции световых пучков, многократно отраженных внутри слоя, который рассматривается как однородная среда, заключенная между двумя однородными, в общем случае различными средами (рис.2.3.)

Рис.2.3. Ход световых лучей в слое.

С практической точки зрения удобно выделить следующие случаи:

- прозрачный слой на прозрачной подложке (при измерении просветляющего и фильтрующего покрытия);

- прозрачный слой на поглощающей подложке (светоделительное, отражающее и фильтрующее покрытие);

- прозрачный слой на прозрачной подложке (светоделительное и отражающее покрытие);

- поглощающий слой на поглощающей подложке (зеркальное отражающее покрытие).

Применительно к полупроводниковым и диэлектрическим материалам главный показатель поглощения k~0,1 и тогда говорят о слабопоглощающем покрытии, или слабопоглощающей подложке.

Прозрачный слой на прозрачной подложке.

(к₂=к₃=0)

При падении световой волны под произвольным углом ₁ на прозрачный слой, нанесенный на поверхность прозрачной подложки, амплитудные коэффициенты отражения (r₁₃) и пропускания (₁₃) системы поверхность подложка-слой, а также выражения для скачка фазы в отраженной (_r)₁₃ и прошедшей (_)₁₃ волнах имеют следующий вид:

(2.9)

(2.10)

tg(_r)₁₃= 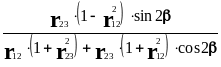(2.11)

tg(_)₁₃= , (2.12)

где () n₂h₂cos₂, а цифровые индексы при величинах r, ,  относятся к средам в соответствии с их нумерацией, причем изменение фазы (_r)₁₃ оценивают на первой границе, а (_)₁₃ - на второй границе. Амплитудные коэффициенты отражения (r_m) и пропускания (r_m+1) на границе раздела двух сред с индексами m и m+1 зависят от направления поляризации падающей волны и вычисляются по общеизвестным формулам Френеля. Для линейной поляризации в плоскости падения и ей перпендикулярной, обозначаемыми соответственно индексами , эти формулы имеют вид:

=-

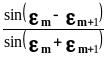
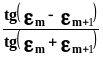=- (2.13)

=

Знаки в правых частях формул (2.13) соответствуют направлению векторов , изображенных на рис.2.4. для случая . Амплитуда отраженной волны для поляризации в плоскости падения меняет знак при , т.е. меняет фазу на 180 . Соответствующий этому случаю угол падения называется углом Брюстера.

Рис.2.4. Направление составляющих в падающей, отраженной и преломленной волнах.

Энергетические коэффициенты отражения и пропускания системы поверхность подложка-слой вычисляют в соответствии со следующими выражениями:

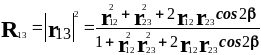(2.14)

(2.15)

При нормальном падении (₁=) амплитудные коэффициенты не зависят от состояния поляризации падающей волны. Формулы (2.13.-2.15) упрощаются и приобретают следующий вид:

(2.16)

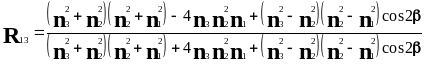(2.17)

(2.18)

Примеры зависимостей и от при ₁=0 для различных n₂ при n₁=1, n₃=1,5 приведены на рис.2.5.

Рис.2.5. Кривые зависимости ( ) и ( ) при ₁ =0.

Прозрачный слой на поглощающей подложке.

(к₂=0, к₃>0)

При отражении световой волны на границе слоя с поглощающей подложкой скачок фазы ₂₃ может принимать любое значение от 0 до  и поэтому амплитудный коэффициент отражения r₂₃ становится комплексной величиной. Энергетический коэффициент системы поверхность подложка-слой в этом случае может быть определен:

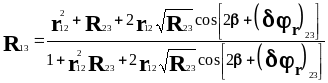(2.19)

где

Комплексный амплитудный коэффициент отражения вычисляется по формулам (2.13) при замене n₃ на n₃=n₃-ik₃.

Изменение фазы при отражении можно определить с помощью следующего выражения:

(2.20)

Поглощающий слой на прозрачной подложке.

(к₂>0, к₃=0)

Для получения соответствующих формул введем следующие дополнительные обозначения:

n₂ ;

, где (2.21)

Используя соотношение (2.21), можно записать выражения для и и соответствующих скачков фазы (_r)₁₃ и (_)₁₃:

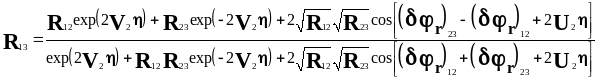(2.22)

(2.23)

(2.24)

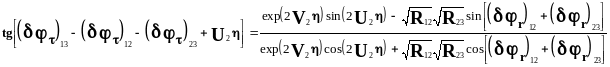(2.25)

Комплексные амплитудные коэффициенты отражения и пропускания

; ;

;

вычисляются по формулам (2.13) при замене n₂ на n₂= n₂-ik₂.

На рис.2.6. представлены зависимости энергетического коэффициента отражения от оптической толщины слоя для нескольких значений k₂. Поглощение в слое уменьшает величину последующих максимумов и вызывает смещение их в направлении меньших толщин.

Рис.2.6. Кривые зависимсти ( n₂ h₂) при различных значениях К₂ (n₁=1, n₂=3,5, n₃=1,5, ₁=).

Поглощающий слой на поглощающей подложке.

(к₂>0, к₃>0)

Для их расчета можно использовать формулы предыдущего раздела при подстановке в них комплексного показателя подложки n₃=n₃-ik₃. При контроле параметров покрытий, соответствующих этому случаю, целесообразно вычислить ряд значений в зависимости от толщины покрытия для различных показателей преломления покрытия и подложки. Полученные расчетные кривые можно использовать для сравнения с экспериментальными данными.