2 .Несобственный интеграл с бесконечными
РАЗРЫВАМИ (2-ГО РОДА).
Определение.
Пусть функция f(x)
задана на полуинтервале [a,b)
и терпит на этом интервале бесконечный
разрыв второго рода в точке b.
Пусть для любого
существует интеграл
.
Несобственным
интегралом второго рода
называется предел
,
т.е.
,
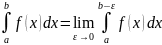при этом, если предел –конечен, то
говорят, что интеграл сходится, если же
предел равен бесконечности или не
существует, то интеграл расходится.
Аналогично вводится понятие несобственного интеграла второго рода для случаев бесконечных разрывов на левом конце и во внутренней точке С интервала (a,b):
(если a
– точка бесконечного разрыва функции
f(x))
(если
и с – точка бесконечного разрыва 2-го
рода)
Если
вычисление первообразной или предела
затруднительно, то применяют теоремы
сравнения, аналогичные теремам сравнения
для несобственных интегралов 1-го рода,
однако сравнение ведется с интегралами
вида
и
.
Эти
интегралы сходятся если p<1
и
расходятся p≥1.
Теорема 4.
Пусть
для всякого 
выполнено
неравенство 
.
Тогда, если интеграл 
сходится,
то интеграл 
сходится,
а если интеграл
расходится,
то интеграл
расходится.
Теорема 5.
Если
f(x)
и g(x)
бесконечно большие одного порядка
роста, то есть 
,
то интегралы
и
сходятся либо расходятся одновременно.
Теорема 6.(Критерий Коши).
Несобственный
интеграл второго рода сходится тогда
и только тогда, когда для всякого ε>0
существует 
такое,
что для всех 
выполняется
неравенство 
Пример
Чтобы определить точки бесконечного разрыва, найдем нули знаменателя.
Так как в промежуток интегрирования [0;2] попадает одна точка бесконечного разрыва подынтегральной функции x=1 , то разобьем исходный интеграл на сумму
Заметим, что так как при вычислении уже первого предела возникла бесконечность, то второй предел можно было не считать.
Если подынтегральная функция имеет на промежутке [a,b] n точек бесконечных разрывов, то количество слагаемых возрастет до n+1, т.е.
.
Такой интеграл будет считаться сходящимся, если каждое слагаемое будет являться сходящимся интегралом.