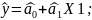- •О выполнении практического задания
- •Описание исходных данных.
- •Предварительный анализ данных.
- •Построение моделей регрессии на всей выборке
- •Регрессионная модель
- •Тесты на гетероскедастичность
- •Тесты на автокорреляцию остатков
- •Тест на нормальность остатков
- •Тест Рамсея
- •Регрессионная модель
- •Регрессионная модель
- •Тесты на гетероскедастичность
- •Тесты на автокорреляцию остатков
- •.Тест на нормальность остатков
- •Тест Рамсея
- •Регрессионная модель
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»
Кафедра математических методов в экономике и управлении
ОТЧЁТ
О выполнении практического задания
по дисциплине Экономика (продвинутый курс)
вариант (тема) 6
Выполнила студентка Сергиенко Алена Валентиновна очной формы обучения
1 курса магистратуры группы Экономика труда 1-1
Проверил:
Писарева Ольга Михайловна
Москва – 2017 г.
Описание исходных данных.
Из файла с заданием были извлечены данные в соответствии с 6 вариантом:
Выборка по наблюдениям |
Выборка по показателям |
|||||||
Первое наблюд-е |
Последнее наблюд-е |
Для прогноза |
Y |
X1 |
X2 |
X3 |
X4 |
|
51 |
100 |
101-103 |
6 |
10 |
11 |
13 |
17 |
|
Rev
|
Assets
|
Curr_Liab
|
Comm_Stock
|
CF_Fin_Act
|
||||
Rev - Выручка, тысяч долл.США
Assets - Активы без учёта оборотных, тысяч долларов США
Curr_Liab - Текущие обязательства, тысяч долларов США
Comm_Stock - Стоимость обыкновенных акций, тысяч доллларов США
CF_Fin_Act - Денежный поток от финансовой деятельности, тыс. дол. США
Таблица исходных данных представлена в Приложении 1.
Предварительный анализ данных.
Построим графики взаимного разброса всех показателей.

1
2
3
4
Рис.1. Графики взаимного разброса переменных
По этим графикам можно сделать следующие выводы:
На графике 2 просматривается линейная взаимосвязь Y и X2, поскольку точки расположены вблизи воображаемой прямой. Связь прямая, поскольку с ростом X2 – Y тоже увеличивается.
На графике 1 в левой стороне расположена точка, которая не вписывается в общую линейную тенденцию взаимосвязи Y и Х1.
На всех четырёх графиках видны «влияющие наблюдения» – это
точки, далеко отстоящие от основного облака точек.
Далее сформируем корреляционную матрицу всех переменных модели.

Рис.2. Корреляционная матрица переменных
Все значения коэффициентов, которые по модулю меньше критического, а именно 0,2787, можно признать незначимыми, или, иными словами, статистически равными нулю.
Исходя из корреляционной матрицы, можно сделать вывод о том, что связи между Y и X1, X2, X3, X4 статистически значимы (так как все коэффициенты по модулю больше критического значения).
Ориентируясь на графики разброса и корреляционную матрицу, получаем следующие варианты моделей парной регрессии, в порядке убывания силы взаимосвязи между Y и фактором:
Построение моделей регрессии на всей выборке
Результаты оценки параметров модели
Регрессионная модель

Рис.3. Результаты оценки регрессии

Модель имеет вид:

Проверим гипотезы о незначимости параметров модели:
Константа
(
Нулевая гипотеза
(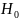 ):
):
 в
генеральной совокупности константа
незначима.
в
генеральной совокупности константа
незначима.
Альтернативная
гипотеза ( ):
):
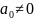 ,
в генеральной совокупности константа
значима.
,
в генеральной совокупности константа
значима.
P – значение = 0,0627 >0,05. Следовательно, нулевая гипотеза не отклоняется с вероятностью (1-0,05) = 0,95, или 95%, то есть константа модели незначима.
Коэффициент
перед X2
(
 ,
в генеральной
совокупности коэффициент перед X2
незначим.
,
в генеральной
совокупности коэффициент перед X2
незначим.
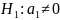 ,
в генеральной
совокупности коэффициент перед X2
значим.
,
в генеральной
совокупности коэффициент перед X2
значим.
P
– значение =
 .
Следовательно,
нулевая гипотеза отклоняется в пользу
альтернативной с вероятностью (1-0,05) =
0,95, или 95%, то есть коэффициент модели
при X2 значим.
.
Следовательно,
нулевая гипотеза отклоняется в пользу
альтернативной с вероятностью (1-0,05) =
0,95, или 95%, то есть коэффициент модели
при X2 значим.
В данном случае незначима константа, из модели ее исключать не будем.
Проверим гипотезу о незначимости модели в целом.
 :
все параметры модели (кроме константы)
равны друг другу и равны нулю, т.е. модель
в целом незначима.
:
все параметры модели (кроме константы)
равны друг другу и равны нулю, т.е. модель
в целом незначима.
: все параметры модели (кроме константы) не равны друг другу и не равны нулю, т.е. модель в целом значима.
P-значение (F) = . Следовательно, нулевая гипотеза отклоняется в пользу альтернативной с вероятностью 95%, то есть модель в целом значима.
Оценка качества модели по графикам

Рис.4. График «прогноз-реализация» для модели

Рис.5. Линия регрессии
Исходя из графика видно, что на нем присутствуют аномальные наблюдения (далеко стоят от прямой регрессии по сравнению с остальными точками). Судя по графику можно предположить, что аномальными являются IOC.BO, ORG.AX, LIN.DE. Для того чтобы точно определить аномальные точки, посмотрим отчет по остаткам.

Рис.6. Выдержка из отчета по предсказанным значениям
Итак, аномальные наблюдения: LIN.DE и ORG.AX. С помощью отчета по значимым наблюдениям определим значимые наблюдения (точки, расположенные вдали от основного облака точек и «натягивающие» регрессионную прямую).

Рис.7. Выдержка из отчета по значимым наблюдениям
Итак, значимые наблюдения: IOC.BO и 0857.НК.
Судя по графику «прогноз – реализация» и графику регрессии - модель
неплохая, однако наличие нескольких аномальных наблюдений увеличивает её стандартную ошибку. Несколько влияющих наблюдений могут сильно влиять на воспроизводимость результатов моделирования: если перестроить модель без них, вероятно, значения параметров модели сильно изменятся.
Проверка наличия ошибок спецификации модели