1.5. Представление чисел в компьютере

Каждый разряд двоичного числа представляется в ЭВМ физическим элементом, обладающим двумя устойчивыми состояниями, одному из которых приписывается значение 0, а другому - 1. Совокупность опреде­ленного количества этих элементов служит для представления многоразрядных двоичных чисел и составляет разрядную сетку или формат пред­ставления числовых данных.

В ЭВМ, как и в математике, используется как естественная, так и нор­мальная формы записи чисел. Каждая из форм имеет определенные форматы для каждого типа ЭВМ, составленные из целого количества байтов. Длину формата данных измеряют в машинных словах или в количестве двоичных разрядов (бит). Например, в вычислительных машинах единой системы ЕС ЭВМ (предшествующих персональным ЭВМ) использовались форматы: полуслово - 2 байта (16 бит), слово - 4 байта (32 бит), двойное слово - 8 байт (64 бит); в персональных ЭВМ: слово - 2 байта, двойное слово - 4 байта.

Естественной формой представления данных обычно называют пред­ставление чисел с фиксированной запятой, положение которой строго устанавливается, для правильных дробей - перед старшим разрядом, для смешанных дробей - в определенном месте, отделяющем целую и дроб­ную части числа, для целых чисел - после младшего разряда. В совре­менных ЭВМ естественная форма используется в основном для пред­ставления целых чисел. Во всех форматах знак числа занимает место перед старшим разрядом и кодируется 0 - знак "плюс" и 1 - знак "минус". Знак от числа отделяется воображаемой точкой.

Рассмотрим диапазон представления чисел в коротком формате Н = 2 байта и в длинном - F = 4 байта (рис 1.1) В разрядных сетках вместе указаны коды наименьшего и наибольшего значений чисел.

Формат Н

Знак 2¹⁴ 2¹³ 2¹ 2⁰

0	0	0	...	0	1
0	1	1	...	1	1
Формат F
0	0	0	...	0	1
0	1	1	...	1	1

Рис 1.1. Форматы чисел в естественной форме

Числа в формате Н имеют значения:

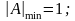
Числа в формате F имеют значения:

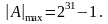
При представлении правильных дробей, например в формате Н, наи­меньшее и наибольшее значения определяются как:

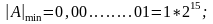
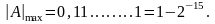
Для сокращения записи двоичных чисел можно использовать шестнадцатеричную систему. Так, в формате

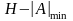= 0001; 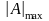= 7FFF,

в формате

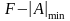= 00000001, = 7FFFFFFF.

Каждая шестнадцатеричная цифра представляет собой двоичную тет­раду.

Пример: Даны 2 числа в форматах Н и F представить числа A=173, B=-173

А₂^H = 0000000010101101; В₂^Н = 1000000010101101;

А₁₆^Н = 00АD; А₁₆^F = 000000АD; В₁₆^Н = 80АD; В₁₆^F = 800000АD.

По первой шестнадцатеричной цифре можно определить знак числа. Если первая цифра меньше 8, то число положительное, если ее значение от 8 до F, то отрицательное.

Достоинствами естественной формы являются простота и наглядность представления чисел, простота алгоритмов реализации операций а, сле­довательно, простота устройств и высокая скорость выполнения опера­ций. Существенным недостатком является ограниченный диапазон пред­ставления величин. Если результаты вычислений выходят за допустимые пределы, то наступает переполнение разрядной сетки и результат иска­жается. В больших машинах вырабатывается при этом запрос на преры­вание программы, а в персональных производится автоматический пере­ход к представлению данных в нормальной форме.

Нормальной формой представления числа называется представление его в виде мантиссы и основания системы в соответствующей степени.

Любое число можно представить в различной форме записи, напри­мер:

А= 55,25 = 5525 *10^-2 = 0,5525 * 10² = 0,005525 * 10⁴.

Любое число в нормальной форме представляется в виде

(1.3)

где m_A- мантисса числа А,

q - основание системы счисления,

Р - порядок.

Для однозначности представления чисел используется нормализован­ная форма, при которой мантисса должна отвечать условию:

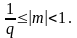(1.4)

Ограничение справа требует, чтобы мантисса представлялась пра­вильной дробью, ограничение слева - чтобы после запятой присутствова­ла значащая цифра (не 0).

Нормальную форму называют также полулогарифмической или с пла­вающей запятой, положение которой определяется порядком, а также экспоненциальной.

Для представления чисел в нормальной форме используются фикси­рованные форматы разной длины. В разрядной сетке форматов отводятся места для знака мантиссы (нулевой разряд), знака порядка (первый раз­ряд), значение порядка (6 разрядов, со 2-го по 7-ой), в остальные разря­ды записывается мантисса числа. В других форматах первый байт не из­меняется, а увеличивается область под мантиссу. На рис. 1.2 представлена разрядная сетка в формате 4 байта.

0	1	2		7	8	9		30	31

Рис. 1.2. Формат числа в нормальной форме

Диапазон представления чисел можно оценить по максимальному значению:

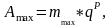
где

При q= 2:

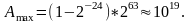
По сравнению с естественной формой диапазон представления чисел при той же разрядной сетке увеличился на 10 порядков.

В ЭВМ ЕС используются три формата: короткий Е (4 байта), длин­ный О (8 байт) и повышенной точности (16 байт). Особенностями нор­мальной формы в ЭВМ ЕС являются следующие:

1. Смещение числовой оси порядков в область положительных значе­ний для облегчения действий над порядками, не имеющими знака. В форматах 7 разрядов отводится под значение порядка и его знак, Сле­довательно, числовая ось порядков находится в диапазоне

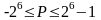или .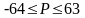

Смещенный порядок, называемый характеристикой, определяется смещением порядка на +2⁶ = 64 = 40₁₆, то есть характеристика Р_х = Р +40

не имеет знака.

Теперь характеристика может принимать значения в диапазоне 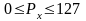=7F₁₆ и под ее значение отводятся 7 разрядов (2⁷ - 1 = 127). Оче­видно, если Р_х = 40, то Р = 0, если Р_х < 40, то порядок отрицательный (Р < 0), при Р_х > 40 - порядок положительный (Р > 0). Если Р_х < 0 или Р_х > 7F, то значение характеристики пропадает и результаты искажаются.

2. Мантиссы и порядки чисел выражаются в шестнадцатеричной сис­теме счисления в двоичном виде, что обеспечивает увеличение диапазона представления чисел, так как изменение характеристики на 1 приводит к сдвигу мантиссы на одну шестнадцатеричную цифру, то есть сразу на одну двоичную тетраду.

Действительно, если в формулу 1.3 подставить q = 16, то

Таким образом, значение порядка увеличилось в 4 раза.

Пример:

Представить в разрядной сетке формата Е два числа:

А = 32008,5₁₀

и

В = -32008,5.

Запишем заданные числа в шестнадцатеричной системе: А = 7D08,8₁₆ и В = -7D08, 8₁₆. Найдем нормализованные мантиссы и характеристики:

m_A=0,7D088,

Р_ха=40+4-44;

m_в=-0,7D088,

Р_хв=40+4=44 (см. рис. 1.3)

Зн.m Р_х m

0	100 0100	0111	1101	0000	1000	1000	0000
1	1000100	0111	1101	0000	1000	1000	0000

0 1 31

Рис. 1.3. Представление чисел в формате Е

А₁₆ = 55700880 > 0, В_1б = С47D0880 < 0

Здесь также по первой шестнадцатеричной цифре кода числа опреде­ляется его знак.