1.1.1. Количество информации

Количество информации - числовая характеристика сигнала, которая не зависит от его формы и содержания и характеризует степень неопре­деленности, которая исчезает после выбора (получения) сообщения в виде данного сигнала.

Р. Хартли предложил в качестве меры неопределенности логарифм от числа возможностей. Обычно количество информации представляется в виде, 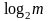, где m - число возможных выборов. Тогда стандартной единицей количества информации будет выбор из двух возможностей. Такая единица получила наименование бит и пред­ставляется одним символом двоичного алфавита, обычно это 0 или 1.

1.2. Системы счисления

Системой счисления называют способ наименования и записи чисел. За время существования человечества были созданы десятки сотен сис­тем счисления. Одни системы можно отнести к позиционным системам, другие к не позиционным, были смешанные системы счисления.

В непозиционных системах количественное значение символа опре­деляется только его изображением и не зависит от его места (позиции) в числе. Например, десятичное число 27 представляется в римской системе счисления

XXVII =10+10+5+1+1,

другими словами, количест­венное значение числа определяется суммой значений символов. Однако значение символа зависит от его места по отношению к другому симво­лу, то есть значение символа неоднозначно. (Например, IX = 9, а XI =11.) В непозиционных системах счисления не представлены дробные и отрицательные числа.

Система счисления называется позиционной, если значение числа в ней определяется как цифрами, принятыми в системе, так и положением (позицией) этих цифр в числе. Закономерность построения позиционных чисел имеет простое математическое представление.

Основание системы - это целое положительное число, большее 1 и равное максимальному количеству различных символов, употребляемых в данной системе счисления. В частности, для десятичной системы счисления q=10.

Введем следующие обозначения:

q - основание системы счисления.

- любая цифра из множества цифр, принятых в данной системе счисления (в случае десятичной системы - любая цифра из множества 0, 1, 2, ..., 9);

i - индекс, который обозначает номер позиции, занимаемой цифрой в числе.

Позицию для целых чисел будем условно обозначать номерами 1, 2, ..., n, а позиции в правильных дробях - номерами -1, -2, ..., - m. Тогда любое число А в произвольной позиционной системе счисления с осно­ванием q может быть записано следующим образом:

(1.1)

где удовлетворяет неравенству

0 < < q – 1 (1.2)

и принимает в этом диапазоне только целые значения, и называется весом i-го разряда. Формулу (1.1) будем называть общей формулой записи числа в позиционной системе счисления с произвольным целым основанием q. Тогда число А в десятичной системе счисления будет иметь вид:

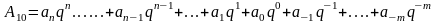
Для десятичной системы счисления понятие веса разряда соответству­ет общепринятым названиям позиций - единицы, десятки, сотни, деся­тые доли, сотые доли и т.д. Например:

1325₁₀ = 1 * 10³ + 3 *10² + 2 * 10¹ + 5 * 10⁰;

67,09₁₀ = 6 * 10¹ + 7 * 10° + 0 * 10^-1 + 9 * 10^-2.