
- •Раздел: «кодирование информации. Системы счисления. Основы алебры логики. Логические основы компьютера»
- •Введение
- •Теоретическая часть глава 1. Кодирование информации. Системы счисления
- •1.1. Понятие информации
- •1.1.1. Количество информации
- •1.2. Системы счисления
- •1.3. Перевод чисел из одной системы счисления в другую
- •1.3.1. Перевод дробных чисел из одной системы счисления в другую
- •1.4. Арифметические операции в позиционных системах
- •1.5. Представление чисел в компьютере
- •1.6. Кодирование текстовой информации. Кодировка ascii.
- •1.6.1. Вычисление информационного объема сообщения.
- •1.6.2. Кодирование и декодирование информации.
- •1.7. Кодирование и обработка графической информации.
- •Глава 2. Основы алебры логики. Логические основы компьютера
- •2.1. Основы логики
- •2.2. Логические выражения и таблицы истинности
- •6) Операция "исключающее или"
- •2.3. Логические законы и правила преобразования логических выражений.
- •2.4. Логические основы компьютера
- •Примеры типовых решений пример решения типового варианта по теме «система счисления» Задача №1
- •Задача №2.
- •Задача №3
- •Задача №4.
- •2 1 0 ← Разряды
- •4 3 2 1 0 ← Разряды
- •Пример решения типового варианта по теме «кодирование информации» Задача №1
- •Задача №2
- •Задача №3
- •Задача №4
- •Задача №5
- •Пример решения типового варианта по теме «алгебра логики» Задача №1
- •Задача №2
- •Задача №3
- •Задача №4
- •Задача №5
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант №20
- •Вариант №13
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант №20
- •Задача №5 Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант №20
- •«Кодирование информации. Системы счисления. Основы алебры логики. Логические основы компьютера»
Задача №2.
Даны
два числа х и у. Чему равна сумма этих
чисел, если
 и
и
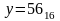 ?
?
1) 1218
2) 1718
3) 6916
4) 10000012
Общий подход: перевести оба исходных числа и ответы в одну (любую!) систему счисления, и выполнить сложение
Решение (вариант 1, через десятичную систему):

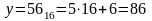
сложение: 35 + 86 = 121
переводим результат во все системы, в которых даны ответы (пока не найдем нужный):
121 = 11110012 = 1718 = 7916
или переводим все ответы в десятичную систему
1218 = 81,
1718 = 121,
6916 = 105,
10000012 = 65
таким образом, верный ответ – 2.
Решение (вариант 2, через двоичную систему):
 (каждая
цифра восьмеричной системы отдельно
переводится
в три двоичных – триаду,
старшие нули можно не писать)
(каждая
цифра восьмеричной системы отдельно
переводится
в три двоичных – триаду,
старшие нули можно не писать)
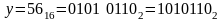 (каждая
цифра шестнадцатеричной системы
отдельно
переводится
в четыре двоичных – тетраду)
(каждая
цифра шестнадцатеричной системы
отдельно
переводится
в четыре двоичных – тетраду)складываем
1000112
+ 10101102
11110012
переводим все ответы в двоичную систему
1218 = 001 010 0012 = 10100012 (по триадам)
1718 = 001 111 0012 = 11110012 (по триадам)
6916 = 0110 10012 = 11010012 (по тетрадам)
10000012 не нужно переводить
правильный ответ – 2.
Решение (вариант 3, через восьмеричную систему):
, никуда переводить не нужно
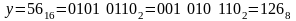 (сначала
перевели в двоичную систему, потом
двоичную запись числа разбили на триады
справа
налево,
каждую триаду перевели отдельно
в десятичную систему, так как для чисел
от 0 до 7 их восьмеричная запись совпадает
с десятичной)
(сначала
перевели в двоичную систему, потом
двоичную запись числа разбили на триады
справа
налево,
каждую триаду перевели отдельно
в десятичную систему, так как для чисел
от 0 до 7 их восьмеричная запись совпадает
с десятичной)складываем
438
+ 1268
1718
видим, что такой ответ есть, это ответ 2.
Решение (вариант 4, через шестнадцатеричную систему):
 (сначала
перевели в двоичную систему, потом
двоичную запись числа разбили на тетрады
справа
налево,
каждую тетраду перевели в шестнадцатеричную
систему; при этом тетрады можно переводить
из двоичной системы в десятичную,
а
затем заменить все числа, большие 9, на
буквы – A,
B,
C,
D,
E,
F)
(сначала
перевели в двоичную систему, потом
двоичную запись числа разбили на тетрады
справа
налево,
каждую тетраду перевели в шестнадцатеричную
систему; при этом тетрады можно переводить
из двоичной системы в десятичную,
а
затем заменить все числа, большие 9, на
буквы – A,
B,
C,
D,
E,
F), никуда переводить не нужно
складываем
2316
+ 5616
7916
переводим в шестнадцатеричную систему все ответы:
1218 = 001 010 0012 = 0101 00012 = 5116 (перевели в двоичную систему по триадам, разбили на тетрады справа налево, каждую тетраду перевели отдельно в десятичную систему, все числа, большие 9, заменили на буквы – A, B, C, D, E, F)
171 2 = 001 111 0012 = 0111 10012 = 7916,
6916, переводить не нужно
10000012 = 0100 00012 = 4116
таким образом, верный ответ – 2.
Задача №3
Пример 1. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход:
вспомним алгоритм перевода числа из десятичной системы в систему с основанием
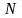 ,
из него следует, что младшая цифра
результата – это остаток от деления
исходного числа на
,
а две младших цифры – это остаток от
деления на
,
из него следует, что младшая цифра
результата – это остаток от деления
исходного числа на
,
а две младших цифры – это остаток от
деления на
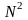 и т.д.
и т.д.в данном случае
 ,
остаток от деления числа на
,
остаток от деления числа на
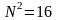 должен быть равен 114
= 5
должен быть равен 114
= 5потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16
Решение (вариант 1, через десятичную систему):
общий вид чисел, которые дают остаток 5 при делении на 16:
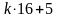
где
 – целое неотрицательное число (0, 1, 2, …)
– целое неотрицательное число (0, 1, 2, …)
среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при
 )
и 21 (при
)
и 21 (при
 )
)таким образом, верный ответ – 5, 21 .
Решение (вариант 2, через четверичную систему, предложен О.А. Тузовой):
переведем 25 в четверичную систему счисления: 25 = 1214, все интересующие нас числа не больше этого значения
из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:
это 114 = 5 и 1114 = 21
таким образом, верный ответ – 5, 21 .
Пример 2. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Общий подход:
здесь обратная задача – неизвестно основание системы счисления, мы обозначим его через
поскольку последняя цифра числа – 2, основание должно быть больше 2, то есть
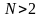
вспомним алгоритм перевода числа из десятичной системы в систему с основанием (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на
Решение:
итак, нужно найти все целые числа
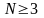 ,
такие, что остаток от деления 23 на
равен 2, или (что то же самое)
,
такие, что остаток от деления 23 на
равен 2, или (что то же самое)
 (*)
(*)
где – целое неотрицательное число (0, 1, 2, …);
сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
из формулы (*) получаем
 ,
так что задача сводится к тому, чтобы
найти все делители числа 21, которые
больше 2
,
так что задача сводится к тому, чтобы
найти все делители числа 21, которые
больше 2в этой задаче есть только три таких делителя:
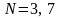 и
и

таким образом, верный ответ – 3, 7, 21 .
