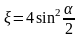Внезапное расширение.

Рисунок 4.1 – Внезапное расширение потока.

При внезапном расширении потока в трубке от сечения 1 до сечения 2 жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы, а также трение внутри вращающихся потоков, вследствие чего происходят существенные потери энергии. Вследствие действия сил инерции потока движущейся жидкости вихреобразование прекращается на некотором достаточно большом расстоянии от зоны выхода жидкости в большее сечение. В результате давление нарастает постепенно.

На рисунке видно, что показания пьезометра во втором сечении больше, чем в первом. Показания пьезометра в данном случае зависят не только от потерь энергии, но и от величины давления. Давление во втором сечении становится больше из-за уменьшения скоростного напора за счёт расширения потока и падения скорости. В этом случае если бы не было потерь напора на местном сопротивлении, то высота жидкости во втором пьезометре была бы ещё больше. Теоретический коэффициент местного сопротивления при внезапном расширении потока равен:

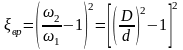(4.4)

если определять по скорости .

Формула для теоретического определения потерь напора при внезапном расширении имеет вид:

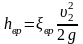(4.5)

Расчетную формулу для теоретического определения потерь напоров применительно к круглым трубам получил также французский инженер Борда.

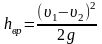(4.6)

т.е. потери напора вследствие внезапного расширения равны скоростному напору потерянной скорости.

Рисунок 4.1 – Внезапное сужение потока

При внезапном сужении, так же как и при внезапном расширении потока, создаются пространства с завихрениями вращающейся жидкости, которые образуются в пристенном пространстве широкой части трубы. Такие же завихрения образуются в начале узкой части трубы за счёт того, что при входе в неё (узкую часть) жидкость продолжает некоторое время двигаться по инерции в направлении центра трубы, и основное русло потока ещё некоторое время продолжает сужаться. Следовательно, при внезапном сужении потока возникает как бы два подряд идущих местных сопротивления. Местное сопротивление за счёт сужения основного русла и сразу же за ним местное расширение, уже рассмотренное выше.

Теоретический коэффициент сопротивления при внезапном сужении потока можно определить по эмпирической зависимости, предложенной И.Е. Идельчиком:

(4.7)

Произведя преобразования и подстановку определённых значений в формулу Борда (4.6) можно получить ещё одну формулу для теоретического определения коэффициента сопротивления при внезапном сужении потока:

, (4.8)

где .

Общей формулой для теоретического определения потерь напора при внезапном сужении потока в обоих случаях будет:

(4.9)

где - безразмерный коэффициент местного сопротивления,

- средняя скорость потока за местным сопротивлением.

Рисунок 4.3 – Поворот потока

Поворот потока (отвод или закруглённое колено) значительно увеличивает вихреобразование и, следовательно, потери энергии. Величина потерь существенно зависит от отношения и угла .