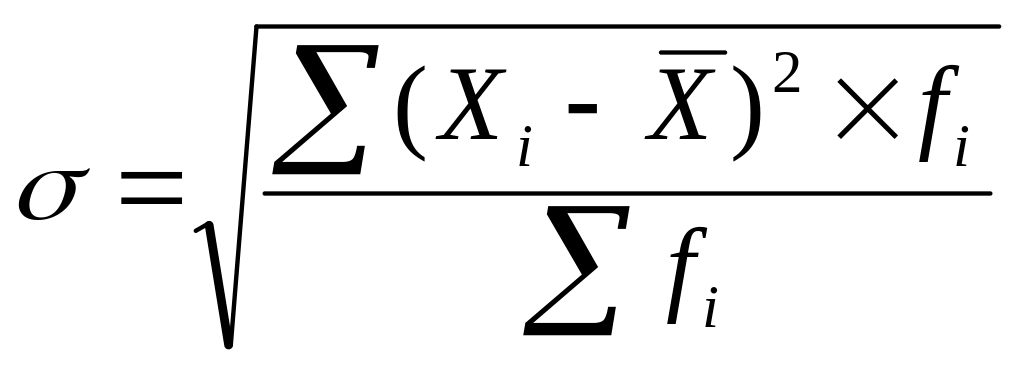3. Средние величины и показатели вариации

Задание 1

С целью изучения затрат времени на обслуживание одного покупателя в магазине бытовой техники было проведено выборочное наблюдение. Результат наблюдения представлен в таблице.

Затраты времени, мин.	Число продавцов, чел
До 5	3
5-7	5
7-9	11
9-11	27
Свыше 11	18

Рассчитать: среднее время на обслуживание одного покупателя; размах вариации; среднее квадратическое отклонение; коэффициент вариации.

Сделать вывод об однородности статистической совокупности и о надежности средней величины.

Решение:

В данном случае необходимо вычислить среднюю интервального ряда. Поэтому в качестве значения признаков в группах принимаются середины интервалов (простая средняя между верхней и нижней границей каждого интервала), в результате чего образуется дискретный ряд.

Если имеются интервалы с открытыми границами (в данной задаче это первый и последний интервал), то для расчета средней в этих условиях условно определяют неизвестную границу интервала. Обычно в этих условиях берут значение последующего интервала (для первого) или предыдущего (для последнего).

С учетом этих замечаний рассчитаем среднюю оценку по формуле средней арифметической взвешенной (т.к. каждое значение признака в исследуемой совокупности встречается неодинаковое число раз)

где x_i – значение признака;

f_i – частота

Вариация признака – различие индивидуальных значений признака внутри совокупности. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом конкретном случае.

Средняя величина – обобщающий показатель совокупности, она не показывает строение совокупности, не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от неё. Для изучения величины отклонений применяют показатели вариации.

1. Размах вариации – наиболее простой измеритель вариации и представляет собой разность между наибольшим (X_max) и наименьшим (X_min) значением признака:

Величина R показывает в каких пределах колеблется размер признака. Показатель указывает на общие размеры вариации, но не дает представления о степени колеблемости внутри совокупности. С помощью размаха вариации определяют допустимые размеры колебаний.

2. Среднее квадратичное отклонение равно корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии:

,

где G² – дисперсия, определяемая по формуле:

- для простых величин;

- для взвешенных величин.

Чем меньше оно, тем лучше среднее значение отражает собой представленную совокупность.

На основании вышеперечисленных показателей вариации рассчитывается показатели относительного рассеивания, а именно коэффициент вариации – процентное соотношение среднего квадратического отклонения к средней величине:

.

Чем больше величина коэффициента вариации, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Если V превышает 40%, то середина рассчитана по неоднородной совокупности и не будет являться типичной для данной совокупности.

Данные для расчета средней величины, размаха вариации, среднего квадратического отклонения и коэффициента вариации представлены в таблице.

Затраты времени, мин.	Величина признака (хi)	Число продавцов, (fi)	xi ×fi	(xi – хср)	(xi – хср)2	(xi – хср)2×fi
До 5	(3+5) / 2 = 4	3	12	-5,625	31,64	94,92
5-7	(5+7)/2 = 6	5	30	-3,625	13,14	65,70
7-9	8	11	88	-1,625	2,64	29,05
9-11	10	27	270	0,375	0,14	3,80
Свыше 11	(11 + 13)/2=12	18	216	2,375	5,64	101,53
Итого	-	64	616	-	-	295

Непосредственно расчет средней величины, размаха вариации, среднего квадратического отклонения и коэффициента вариации представлены в таблице.

Показатель	Формула расчета	Значение
Средние затраты времени, мин		= 9,625
Среднее квадратическое отклонение		= 2,15
Коэффициент вариации		= 22,31
Размах вариации		12 – 4 = 8

Вывод: средние затраты времени на обслуживание одного покупателя в магазинах бытовой техники составляют 9,625 минут. При этом время на обслуживание клиентов может колебаться от 4 до 12 минут (т.е. допустимый размах колебаний составляет 8 минут). Данная совокупность является однородной: значение коэффициента вариации (22%) не превышает пороговое значение в 40%.

Таким образом, рассчитанное среднее время на обслуживание одного клиента является типичной для данной совокупности.

Задание 2

Имеются данные о численности работников предприятия на начало каждого квартала года. Определить средние характеристики динамического ряда: средний уровень ряда (средняя численность работников), средний абсолютный прирост и средний темп роста и прироста. Указать виды средних, которые были использованы.

Кварталы	Первый	Второй	Третий	Четвертый	Первый следующего года
Численность работников на начало квартала, чел.	300	310	315	328	330

Решение:

1. Определим среднюю численность работников по средней хронологической, т.к. известны данные на начало каждого квартала (это моментный временной ряд):

,

где Т₁, Т₂, Т₃, Т₄, Т₅ – численность работников на начало каждого квартала;

n – число кварталов.

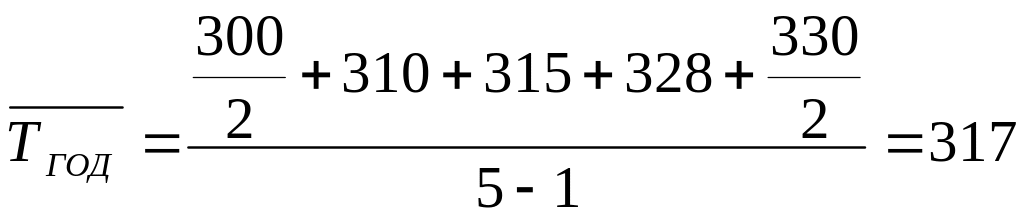чел.

Таким образом, средняя численность работников по предприятию в течение года составила 317 человек.

Задание 3

Данные по предприятиям объединения, выпускающим однородную продукцию, за два периода:

Предприятие	Базисный период		Отчетный период
	Затраты времени на единицу продукции, ч (xi)	Произведено продукции, тыс. шт. (fi)	Затраты времени на единицу продукции, ч (xi)	Затраты времени на всю продукцию, тыс. ч (Wi)
1-е	4	30	3	99
2-е	5	50	4	216
3-е	3	70	3	222

Рассчитайте затраты времени на производство единицы продукции в среднем по объединению за каждый период. Обоснуйте применение формул средних для расчета заданных показателей. Сделайте выводы.

Решение:

Средние затраты времени на производство единицы продукции определяются как отношение затрат времени на производство всей продукции к объему произведенной продукции.

Затраты на производство всей продукции определяются как произведение количества произведенной продукции (частоты) и времени, которое затрачивает на производство единицы продукции (признак).

Для расчета средних затрат времени на производство единицы продукции в базисном можно использовать формулу средней арифметической взвешенной. Здесь выделен признак и его частота, и признак в исследуемой совокупности встречается неодинаковое число раз. Кроме того, в логической формуле средней не известен числитель.

, где

x_i – значение признака;

f_i – частота.

Средние затраты времени на производство единицы продукции в базисном периоде составят:

часа

Затраты на производство всей продукции определяются как произведение количества произведенной продукции и времени, которое затрачивает на производство единицы продукции. В этом случае в формуле расчета средней не известен знаменатель, поэтому логично использовать формулу средней гармонической.