Математическая модель структуры системы
Структуры систем могут быть описаны различными способами, к основным из которых относятся: графический, списочный, матричный, графовый и теоретико-тождественный [].
Для систем управления предприятием, имеющим множество связей с производством, с вышестоящими организациями, наиболее наглядным является графовое представление структуры, задаваемое множеством вершин (элементов) X1, множеством рёбер (связей)U, с выделенным подмножеством краевых рёберU0и отношением инцидентности рёбер и вершинE. Графически вершины изображаются точкой, ориентированное ребро - направленным отрезком, неориентированное ребро - отрезком. С краевыми рёбрами можно связать фиктивные вершины, называемые полосами структуры. Тогда множество вершинX1можно доопределить:X = X1X0, гдеX0 - множество фиктивных вершин,|X0| = | U0|, | |- мощность множества, а структуру системы представить в виде тройки.
C = <X, U : E>,
где E-предикат, определённый на всех таких упорядоченных тройкахx,u,y, для которыхx,yX,uUи обладающий свойством,
uU x, yX {E(x, u, y) &
x’, y’X [E(x’, u, y’) (x = x’ & y = y’) (x = y’ & y = x’)]},
означающим, что любая дуга u, принадлежащая множеству U, соединяет только две вершины x и y,принадлежащие множеству X.
Использование трёхместного предиката E для представления мультиграфа позволяет легко перейти к списочному способу описания, являющемуся наименее избыточным при решении задач преобразования структур на ЭВМ.
Подмножества
представляют
собой множества ориентированных рёбер
(
),
петель (
)
и неориентированных рёбер (
).
Операции над структурами, композицией которых можно добиться любого желаемого изменения структуры в нужном направлении приведены ниже в таб. 2.
Операции по преобразованию структур
Таблица 2.
|
Название операции |
Описание операции |
Графическое представление |
x, y uU1 |
C1 = <X1, U1; E> C2 = <X2, U2; E> X2 = (X1\{x, y}){z}, U2 = U1 u1Ux, u2Uy u1, u2Uz Ux = {uU| E(, u, x) E(x, +u, )} |
z={x,y} |
u1, u2 u1Ux & u1Uy u2Ux & u2Uy E(x, u1, y) & E(x, u2, y) |
C1 = <X1, U1; E> C2 = <X2, U2; E> X2 = X1, U2 = (U1\{u1, u2}){u} uUx & uUy & E(x, u, y) |
|
uUx & uUy E(x, u, y) |
C1 = <X1, U1; E> C2 = <X2, U2; E> X2 = X1{x01, x02}, U2 = (U1\{u}){u1, u2} u1Ux, u2Uy E(x, u1, x01) & E(x02, u2, y) |
|
E(x, u, y)
|
C1 = <X1, U1; E> C2 = <X2, U2; E> X2 = X1, U2 = U1{u}, E(x, u, y) Uxc2 = Uxc1{u}, Uyc2 = Uyc1{u} |
|
|
C1 = <X1, U1; E> C2 = <X2, U2; E> X2 = X1, U2 = U1\{u} Uxc2 = Uxc1\{u}, Uyc2 = Uyc1\{u} |
|
|
C1 = <X1, U1; E> C2 = <X2, U2; E> X2 = X1{x}, U2 = (U1\{u}){u1, u2} uUz & uUy u1Uz, u2Uy E(z, u1, x) & E(x, u2, y) |
|
E(x1,u1,x) &E(x,u2,x2) |
C1 = <X1, U1; E> C2 = <X2, U2; E> X2 = X1\{x}, U2 = (U1\{u1, u2}){u} E(x1, u, x2) |
|
E(x, u1, y) & E(x, u2, y) |
C1 = <X1, U1; E> C2 = <X2, U2; E> X2 = (X1\{x}){x1, x2}, U2 = U1 u1Ux1 & u1Ux2, u2Ux2 & u2Ux1 |
|
E(x1, u, x2) |
X2 = X1, U2 = (U1\{u}){u1, u2} E(x1, u1, x2) & E(x1, u2, x2) |
|
|
C = <X, U; E> C2 = <X2, U2; E> X2 = (X\X1){x}, U2 = (U\U1)U01 Ux = U01, где U01 - множество краевых рёбер структуры C1 |
|
C1 = <X1, U1; E> и C2 = <X2, U2; E> |
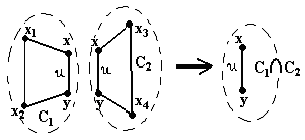
С1С2 C3 = <X3, U3; E> X3 = X1X2, U3 = U1U2 |
|
C1 = <X1, U1; E> и C2 = <X2, U2; E> |
С1С2 C3 = <X3, U3; E> X3 = X1X2, U3 = U1U2 |
|
C1 = <X1, U1; E> и C2 = <X2, U2; E> X1X2 = {x01, x02} |
С1-С2 C3 = <X3, U3; E> X03 = X01(X02\{x01, x02}) X3 = (X1\X01)(X2\X02)X03 U03 = U01(U02\{u01, u02}) U3 = (U1\U01)(U2\U02)U03{u} |
|
C2 = <X2, U2; E> до структуры C1 = <X1, U1; E> |
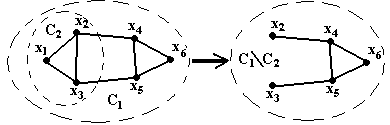
С1\С2 C3 = <X3, U3; E> X3 = X1\X2, U3 = U1\U2
|
|
Набор операций перечисленный в табл. 2 позволяет сделать преобразование структуры в нужном направлении.