Разбиение графа на подграфы с минимальной связностью.
существует тривиальный прием решения - перебор всех возможных вариантов разбиения графа и выбор из них оптимального разбиения.
Если число вершин в
графе
,
то число сочетаний
существуют алгоритмы направленного( упорядоченного ) перебора.
Алгоритмы:
предлагает решать целочисленную задачу квадратичного программирования с минимизацией суммы внешней связи между подграфами. Такая задача решается методом ветвей и границ, где на каждом шаге ветвления решаются линейные задачи;
алгоритм эвристический.
Суть первого алгоритма состоит в следующем:
если нам необходимо
разрезать граф, заданный матрицей
смежности на
подграфов, то эту процедуру сводят к
последовательному разрезанию на 2
подграфа.
Для реализации этой
цели выделяют в матрице
две
подматрицы. Размерность подматриц
равна числу вершин первого и второго
подграфов.
Для каждой строки
матрицы
подсчитывают числа внешней связности
-
и числа внутренней связности -
.
Эти числа подсчитывают следующим образом:
,
- количество вершин,
которые будут в первом подграфе.
.
Пример.
Имеется граф, содержащий 9 вершин. Требуется разбить его на 3 подграфа по 3 вершины в каждом.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
1 |
2 |
0 |
3 |
0 |
1 |
0 |
2 |
|
2 |
1 |
0 |
0 |
1 |
0 |
2 |
0 |
3 |
1 |
|
3 |
2 |
0 |
0 |
2 |
1 |
3 |
1 |
2 |
1 |
|
4 |
0 |
1 |
2 |
0 |
0 |
1 |
2 |
1 |
0 |
|
5 |
3 |
0 |
1 |
0 |
0 |
2 |
1 |
0 |
3 |
|
6 |
0 |
2 |
3 |
1 |
2 |
0 |
1 |
2 |
3 |
|
7 |
1 |
0 |
1 |
2 |
1 |
1 |
0 |
0 |
1 |
|
8 |
0 |
3 |
2 |
1 |
0 |
2 |
0 |
0 |
2 |
|
|
2 |
1 |
1 |
0 |
3 |
3 |
1 |
2 |
0 |
9
После вычисления
чисел: числа внешней связности -
и числа внутренней связности -
вычисляются элементы вспомогательной
матрицы по следующей формуле:
.
Получают матрицу
.
Элементы этой матрицы характеризуют
изменение числа связей при перестановке
вершин
и
.
Анализируя матрицу
находим
максимальный элемент
.
При наличии нескольких одинаковых
максимальных элементов выбирается
один из них(любой). Осуществляется
перестановка в матрице
столбцов и строк с номерами
и
.
Получим
.
Для матрицы
снова вычисляем числа
и
и строим матрицу
.
Если в матрице
нет положительных элементов, то из
исходного графа удаляем подграф, который
соответствует матрице смежности из
вершин. Для рассмотрения остается
матрица размером
.
Если в матрице
есть положительные элементы, то повторяем
процесс.
Пример.
( продолжение )
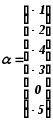
Построим теперь матрицу
:
4 5 6 7 8 9
-
-1
-2
-4
-3
0
-5
3
2
-5
-1
-2
3
-6
1
6
3
4
-2
3
0
-1
2
8
3
4
-2
3
4
1
3
4 - максимальный элемент. Выбранный элемент (3, 5) - произвольный из трех максимальных элементов.
Меняем местами 3 и 5 строки и столбцы в исходной матрице.
|
|
1 |
2 |
5 |
4 |
3 |
6 |
7 |
8 |
9 |
|
1 |
0 |
1 |
3 |
0 |
2 |
0 |
1 |
0 |
2 |
|
2 |
1 |
0 |
0 |
1 |
0 |
2 |
0 |
3 |
1 |
|
5 |
3 |
0 |
0 |
0 |
1 |
2 |
1 |
0 |
3 |
|
4 |
0 |
1 |
0 |
0 |
2 |
1 |
2 |
1 |
0 |
|
3 |
2 |
0 |
1 |
2 |
0 |
3 |
1 |
2 |
1 |
|
6 |
0 |
2 |
2 |
1 |
3 |
0 |
1 |
2 |
3 |
|
7 |
1 |
0 |
1 |
2 |
1 |
1 |
0 |
0 |
1 |
|
8 |
0 |
3 |
0 |
1 |
2 |
2 |
0 |
0 |
2 |
|
9 |
2 |
1 |
3 |
0 |
1 |
3 |
1 |
2 |
0 |
Получаем матрицу
.
Для матрицы
снова вычисляем числа
и
и строим матрицу
.
Построим теперь матрицу
:
4 3 6 7 8 9
-
-5
-6
-6
-3
-4
-1
1
-4
-9
-5
-4
-3
-4
1
6
-1
0
-4
3
-4
3
2
4
-1
-4
-6
-1
0
-3
5
3 - максимальный элемент. Выбранный элемент (2, 9) - произвольный из двух максимальных элементов.
Меняем местами 2 и 9 строки и столбцы в исходной матрице.
|
|
1 |
9 |
5 |
4 |
3 |
6 |
7 |
8 |
2 |
|
1 |
0 |
2 |
3 |
0 |
2 |
0 |
1 |
0 |
1 |
|
9 |
2 |
0 |
3 |
0 |
1 |
3 |
1 |
2 |
1 |
|
5 |
3 |
3 |
0 |
0 |
1 |
2 |
1 |
0 |
0 |
|
4 |
0 |
0 |
0 |
0 |
2 |
1 |
2 |
1 |
1 |
|
3 |
2 |
1 |
1 |
2 |
0 |
3 |
1 |
2 |
0 |
|
6 |
0 |
3 |
2 |
1 |
3 |
0 |
1 |
2 |
2 |
|
7 |
1 |
1 |
1 |
2 |
1 |
1 |
0 |
0 |
0 |
|
8 |
0 |
2 |
0 |
1 |
2 |
2 |
0 |
0 |
3 |
|
2 |
1 |
1 |
0 |
1 |
0 |
2 |
0 |
3 |
0 |
Получаем матрицу
.
Для матрицы
снова вычисляем числа
и
и строим матрицу
.
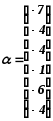
Построим теперь матрицу
:
4 3 6 7 8 2
-
-7
-4
-4
-1
-6
-4
-1
-8
-9
-5
-4
-7
-7
1
3
-4
-3
-7
0
-7
-3
9
-2
-9
-8
-10
-5
-8
-6
5
Поскольку в матрице
нет
положительных элементов, то из исходного
графа удаляем подграф, соответствующий
матрице смежности из трех вершин. Для
рассмотрения остается матрица размерности
6.
Полученный подграф -
.
Теперь рассматриваем матрицу:
|
|
4 |
3 |
6 |
7 |
8 |
2 |
|
4 |
0 |
2 |
1 |
2 |
1 |
1 |
|
3 |
2 |
0 |
3 |
1 |
2 |
0 |
|
6 |
1 |
3 |
0 |
1 |
2 |
2 |
|
7 |
2 |
1 |
1 |
0 |
0 |
0 |
|
8 |
1 |
2 |
2 |
0 |
0 |
3 |
|
2 |
1 |
0 |
2 |
0 |
3 |
0 |
Получаем матрицу
.
Для матрицы
снова
вычисляем числа
и
и строим матрицу
.
Построим теперь матрицу
:
7 8 2
-
4
2
0
1
1
1
-1
4
-2
0
-4
-2
3
1
3
-1
-3
6
3 - максимальный элемент. Выбранный элемент (6, 7).
Меняем местами 6 и 7 строки и столбцы в исходной матрице.
|
|
4 |
3 |
7 |
6 |
8 |
2 |
|
4 |
0 |
2 |
2 |
1 |
1 |
1 |
|
3 |
2 |
0 |
1 |
3 |
2 |
0 |
|
7 |
2 |
1 |
0 |
1 |
0 |
0 |
|
6 |
1 |
3 |
1 |
0 |
2 |
2 |
|
8 |
1 |
2 |
0 |
2 |
0 |
3 |
|
2 |
1 |
0 |
0 |
2 |
3 |
0 |
Получаем матрицу
.
Для матрицы
снова вычисляем числа
и
и строим матрицу
.
Построим теперь матрицу
:
6 8 2
-
1
-2
-4
-1
-2
-5
-7
4
2
-3
-4
-2
3
-2
-3
-4
-6
7
Поскольку в матрице
нет
положительных элементов, то из исходного
графа удаляем подграф, соответствующий
матрице смежности из трех вершин. Для
рассмотрения остается матрица размерности
3.
Полученный подграф -
.
Теперь рассматриваем матрицу:
|
|
6 |
8 |
2 |
|
6 |
0 |
2 |
2 |
|
8 |
2 |
0 |
3 |
|
2 |
2 |
3 |
0 |
Полученный подграф -
.
Таким образом исходный граф из 9 вершин разбит на 3 подграфа по 3 вершины в каждом. Получили:
.
Сделали 5 итераций.
Число внешних связей
между подграфами
.