86

9. Задачи дискретной оптимизации.

   1. Методы решения задач дискретной оптимизации.

Развитие методов решения задач дискретной оптимизации обусловлено теоретической и практической важностью этих задач, встречающихся в различных областях науки и техники. Развитие методов идет в основном по пути создания новых численных методов для решения как общих задач дискретного программирования (оптимизации), так и задач частного вида.

Существующие сейчас методы дискретного программирования по способу достижения оптимума можно разделить на три основных вида:

1. методы отсечения;

2. комбинаторные методы;

3. приближенные методы.

На основе этих методов иногда разрабатываются гибридные методы.

Интенсивное развитие получили комбинаторные методы. Это вызвано тем, что на практике необходимо решать большое количество оптимизационных, комбинаторных задач. Такими задачами, к примеру, являются:

1. задача о ранце;

2. задача о коммивояжере;

3. задача минимизации среднего времени обработки партии деталей;

4. задача о назначениях;

5. задача о покрытии;

6. задача компоновки;

и так далее.

Определить понятие оптимизационно-комбинаторной задачи можно следующим образом:

пусть имеется множество из n элементов. На этом множестве задается множество комбинаций , где под комбинациями понимаются сочетания, подстановки, перестановки, свойственные каждой задаче. На множествезадается функция. В оптимизационно-комбинаторной задаче ищется экстремум(максимум или минимум) и отыскиваются те элементы множества, на которых функцияэкстремальна.

При решении оптимизационно-комбинаторных задач:

1. нужно уметь перебирать множество значений функции ;

2. вычислять эти значения и сравнивать.

Для решения оптимизационно-комбинаторных задач было разработано большое число алгоритмов, общая идея которых состоит в замене полного перебора всех вариантов частичными переборами меньших объемов.

Для осуществления этого производится отбрасывание некоторых подмножеств, заведомо не содержащих искомого экстремума и сужении области перспективных вариантов. При этом получаются весьма разнообразные методы, определяемые структурой соответствующих конечных множеств .

В настоящее время наиболее широко применяемыми являются три группы методов:

1. локальная оптимизация;

2. случайный поиск;

3. метод ветвления.

Рассмотрим кратко суть этих методов.

При локальной оптимизации для каждой комбинации определяется множество- множество комбинаций, соседних с. Исходной операцией является случайный выбор начальной комбинации. Затем в множественаходят локальный экстремум. Этот процесс повторяется многократно и среди полученных локальных экстремумов выбирается наименьший и именно он принимается за приближенное значение.

Случайный поиск.

При случайном поиске выбор всех комбинаций происходит случайно согласно некоторому закону распределения. Значения целевой функции на этих комбинациях вычисляются и среди них выбирается та комбинация, которая дает экстремальное значение целевой функции. Основной проблемой при случайном поиске является выбор существенных признаков комбинаций. Существуют два подхода:

1. признаки выбираются заранее путем анализа условий задачи;

2. признаки получают из анализа уже полученных решений.

Методы ветвления.

Впервые метод ветвей и границ был предложен для решения задач целочисленного линейного программирования.

В дальнейшем этот метод был применен в более общим классам комбинаторных оптимизационных задач. По способу ветвления все алгоритмы ветвей и границ можно разделить на следующие группы:

1. алгоритмы, строящие дерево подзадач исходной задачи(например, алгоритм Лэнд и Дойга, предложенный для решения задач целочисленного программирования. В этом методе строится дерево задач линейного программирования, добиваясь постепенного удовлетворения условий целочисленности);

2. алгоритмы, строящие дерево недопустимых решений(например, аддитивный алгоритм Балаша и его модификации). Этот метод применяется для решения задач линейного программирования с булевыми переменными;

3. алгоритмы, строящие дерево допустимых решений(например, метод решения задач о коммивояжере).

Общая схема метода ветвей и границ для задачи дискретной оптимизации

(9.1.0 )

,- допустимое, конечное множество (9.1.0 )

включает следующие основные моменты:

1. подсчет оценок (ищется нижняя граница целевой функции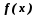на множестве). Нижней оценкой будет такое число, что;

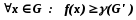2. многошаговый процесс разбиения множества на подмножества(ветвление по определенным правилам);

3. пересчет оценок. Если множество , то. Если множествосостоит из объединения, то есть, то оценка для любого подмножествабудет не меньше, чем оценка для множества, то есть:

.

Часто для некоторых удается получить строгое неравенство:

4. признак оптимальности(в том случае когда решаем задачу на минимум)

в случае, если и(x - решение, принадлежит некоторому ) и,

то x - оптимальное решение задачи ( 9.1 .0 ) - ( 9.1 .0 ).

Процесс решения исходной задачи ( 9.1 .0 ) - ( 9.1 .0 ) может быть описан так:

1. вычислить оценку . Если удается найти такоеx, что , тоx - оптимальное решение. Если оптимальное решение не обнаружено, то по некоторому правилу разбиваем множество на подмножества;

2. считаем оценки множеств. Если при этом удается найти такоеx, что ,, тоx - оптимальное. Если такого x не обнаружили, то для дальнейшего разбиения выбираем множество с минимальной оценкой. Разбиваем это множество на несколько подмножеств и повторяем процесс до тех пор, пока не получим оптимальное решение.