Лекции / ЭЛЕМЕНТЫ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

ЭЛЕМЕНТЫ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Оптимизация непрерывных систем.

Выше говорилось о существовании обширного клас­са экономических и технических задач, в которых необ­ходимо отыскать управление, представляющее собой некоторый многошаговый процесс принятия решения. Примером таких многошаговых процессов является управление дискретными системами, изменяющими свое состояние в соответствии с принятым управлением в не­которые дискретные моменты времени. Для решения задач оптимизации в таких системах предложен разра­ботанный Р. Беллманом метод, получивший название динамического программирования.

Б основу метода положен интуитивно очевидный принцип, названный принципом оптимальности. В соот­ветствии с этим принципом оптимальное управление определяется конечной целью управления и состоянием системы в рассматриваемый момент времени.

Приведем формулировку принципа оптимальности. Оптимальное поведение обладает тем свойством, что ка­ковы бы ни были первоначальное состояние и решение е начальный момент, последующие решения должны со­ставлять оптимальное поведение относительно состоя­ния, получающегося в результате первого решения.

При использовании этого принципа оказывается воз­можным исходную сложную проблему отыскания много­шагового управления заменить последовательным ре­шением некоторого количества существенно более про­стых одношаговых задач оптимизации.

Смысл принципа оптимальности становится более ясным, если понять, что для любой оптимальной траек­тории каждый ее участок, связывающий любую проме­жуточную точку этой траектории с конечной, также является оптимальной траекторией.

Применим принцип оптимальности для оптимизации управления в непрерывных системах.

Рассмотрим задачу о минимизации функционала

(14.1)

для системы, поведение которой описывается совокупно­стью дифференциальных уравнений вида.

(14.2)

В соотношениях (14.1) и (14.2) использованы сле­дующие обозначения: — вектор из области допустимых значений параметров системы, характеризующий состоя­ние системы в данный момент времени; — вектор управления из области допустимых управлений Ω, В начальный момент времени t= 0, =_н, время Т фиксировано.

Пусть в некоторый момент времени 0<τ<Т состоя­ние системы характеризуется вектором (τ). Начиная с момента времени τ, в течение временного интервала продолжительностью Δτ используем некоторое произ­вольное управление u_Δ (t) Ω. Тогда в соответствии с (14.2) в момент времени τ + Δτ система будет нахо­диться в точке

Будем считать теперь, что, начиная с момента времени τ + Δτ и до конца, т.е. до t = T, используется опти­мальное управление

Обозначим через J*(t) минимальное значение функционала (14.1) при оптимальном управлении *(τ) (при ), т. е.

Тогда значение функционала (14.1) при использова­нии управления

может быть найдено из соотношения

Понятно, что ввиду неоптимальности управления _Δ (t)

(14.3)

При этом равенство в (14.3) может быть получено только, если в качестве _Δ (t) будет использовано оптимальное управление, т. е.

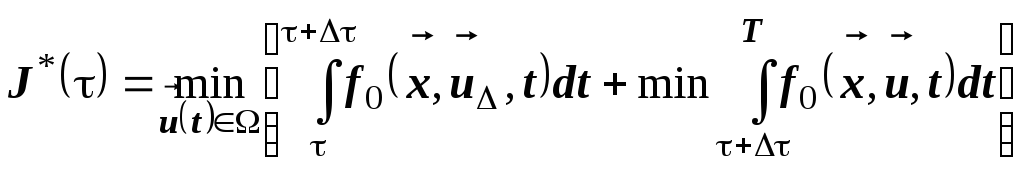(14.4)

С точностью до бесконечно малых более высокого поряд­ка, чем Δτ можно считать, что

С учетом этого, меняя τ на t, перепишем (14. 4) в виде

(14.5)

Допустим теперь, что функция J(t) имеет частные производные по всем координатам и по времени t. Тог­да, разлагая J*(t) в ряд Тейлора, имеем с точностью до бесконечно малых первого порядка:

(14.6)

(14.7)

Имея в виду (14.7), подставим (14.6) в (14.5). При этом

(14.8)

Принимая во внимание, что J*(t) и, следовательно, δJ*(t)/δt не зависит от (t), получаем

(14.9)

Полученное нелинейное дифференциальное уравнение в частных производных называют уравнением Беллмана. С помощью этого уравнения во многих случаях опти­мальные управления и траектории могут быть получены аналитически.

Заметим, что если функционал (14.1) не зависит явно от времени, т. е. δJ/δt=0, то требования для *(t), вытекающие из уравнения Беллмана для отыскания оптимального управления, совпадают с условиями прин­ципа максимума.

В самом деле, в этом случае уравнение (14.9) при­обретает вид

(14.10)

Выберем теперь вектор-функцию следующим об­разом:

(14.11)

Тогда функция Гамильтона запишется в виде

Поскольку

основное условие принципа максимума совпадает с (14.10).

Как вполне очевидно, эквивалентность уравнений ди­намического программирования и принципа максимума может иметь место, только если существуют частные производные от функционала J*, что является необхо­димым условием построения уравнения Беллмана (14.9). Поскольку предположение о существовании частных производных от J* справедливо далеко не всегда, об­ласть применения динамического программирования для оптимизации непрерывных систем значительно уже области применения принципа максимума.

Вместе с тем, нельзя не отметить, что метод динами­ческого программирования оказывается весьма эффек­тивным при решении дискретных оптимизационных за­дач.

Оптимизация дискретных систем

Пусть система может находиться в одном из состоя­ний дискретного множества S. Множество S можно трактовать как дискретное фазовое пространство. Для каждого из возможных состояний определим множе­ство допустимых управлений ,. Система может переходить из одного состояния в другое. При этом будем считать, что система обладает марковским свойством, т. е. будущее состояние системы зависит только от со­стояния, в котором находится система в настоящий мо­мент времени, и используемого в этот момент управле­ния. В соответствии с этим введем функцию переходов, используя которую, запишем рекуррентное соотношение, определяющее эволюцию системы

(14.12)

Здесь — состояние системы на i-м шаге.

Тогда N-шаговому управлению можно поставить в соответствие траекторию движения системы

если задано — начальное состояние-системы.

Качество выбранного управления можно характери­зовать численным значением целевой функции , зависящим от траектории системы в пространстве S.

Задача состоит в выборе-управления u, доставляю­щего экстремум выбранному критерию. Для простоты будем считать, что критерий аддитивен относи­тельно множества состояний, пробегаемых в процессе эволюции системы, т. е.

(14.13)

Введем функцию , равную численному значению критерия (14.13) при оптимальном k-шаговом управлении, начиная из состояния . Предположим, что система находится в некотором состоянии и над­лежит выбрать одношаговое управление таким обра­зом, чтобы максимизировать (14.13). Тогда

(14.14)

Пусть теперь система находится в состоянии и надлежит выбрать оптимальное двухшаговое управле­ние так, чтобы максимизировать (14.13). Тогда в соответствии с принципом оптимальности

Рассуждая аналогично, имеем

(14.15)

откуда, в частности,

(14.16)

Вычислительная процедура решения задачи теперь ясна. Отыскание оптимального управления начинаем с последнего шага. При этом для каждого из возмож­ных состояний системы , используя (14.14), необ­ходимо отыскать и запомнить оптимальное управление .Таким образом, будет известно оптимальное одношаговое управление для любого из возможных со­стояний системы. Теперь, используя (14.15) при k=2, для каждого из возможных состояний системы найдем оптимальное двухшаговое поведение . Обра­тим внимание на то, что при этом фактически прихо­дится решать одношаговую оптимизационную задачу отыскания , так как после отыскания с ис­пользованием соотношения (14.12) вычисляется состоя­ние , причем для каждого из оптимальное управ­ление уже было найдено ранее. Аналогично отыскивает­ся оптимальное поведение для k = 3, 4, ..., N-1. Поскольку начальное состояние системы фиксирова­но, при отыскании оптимального управления на первом шаге нет необходимости решать оптимизационную задачу для всех . Нужно сделать это только для исходного состояния .

Таким образом, метод динамического программиро­вания позволяет отыскать оптимальное многошаговое управление путем решения совокупности более простых одношаговых оптимизационных задач.

Поясним вычислительную процедуру метода на сле­дующих примерах.

Задача 1. На рис. 14.1 изображена сеть, соединяющая точки А и В. Сеть состоит из совокупности узлов S и соединяющих их дуг. Каждой дуге, соединяющей два каких-либо узла сети, приписано число, характеризующее продолжительность перехода по этой дуге. Необходимо отыскать кратчайший по времени путь из A в В, если разрешенным является только движение слева направо.

Решение. Составим таблицу, в которой будем хранить опти­мальное управление и соответствующее ему значение целевой функ­ции для всех возможных состояний системы после каждого шага. Число строк таблицы равно числу шагов N процесса управления

(в рассматриваемом примере N=4). Число столбцов таблицы равно числу возможных состояний (в рассматриваемом примере конечное состояние фиксировано, поэтому число столбцов на единицу меньше числа возможных состояний и равно 12).

k
	1	2	3	4	5	6	7	8	9	10	11	12
1	---	---	---	---	---	---	---	---	13/12	13/8	13/6	13/7
2	---	---	---	---	12/11	11/12	12/10	11/16	---	---	---	---
3	---	5/22	5/18	6/15	---	---	---	---	---	---	---	---
4	3/24	---	---	---	---	---	---	---	---	---	---	---

Клетки таблицы разбиты пополам, причем слева вверху будем хранить оптимальное управление, а справа внизу — соответствующее значение целевой функции. Для каждого узла сети управление однозначно определяется номером следующего на выбранном маршруте узла. В первой строке таблицы хранится информация о последнем шаге пути.

Поскольку перед последним (четвертым) шагом множество воз­можных состояний есть

и из каждого из этих состояний ведет лишь один путь в В, оптимальное управление очевидно. При этом

Перед предпоследним (третьим) шагом множество возможных состояний системы .

Как видно из рисунка,

Пусть состояние системы перед двумя последними шагами есть :

Так как

то = min {6+12, 4+7} = 11, причем . Таким образом, установлено, что если система находится в со­стоянии , то оптимальное поведение на очередном шаге состоит в переходе в состояние , после чего ранее найденное оптимальное управление обеспечивает кратчайший переход в конечное состояние. Продолжительность пути из в равна 11 единицам. Продолжая аналогично, заполняем вторую и третью строки таблицы. Поскольку начальное состояние задано, четвертая строка содержит один эле­мент. При этом

Тогда

причем .

Теперь не представляет никакого труда определить оптимальное многошаговое управление. На первом шаге . При этом мы попадаем в состояние , для, которого оптимальное управление уже найдено и . После второго шага состояние системы есть и оптимальное управление на третьем шаге . Из состояния в ведет один путь.

Таким образом, кратчайший маршрут из A в В имеет вид и его продолжительность равна 24 единицам.