
- •1. Состоятельность оценки –
- •2. Несмещенность оценки
- •3. Эффективность оценки
- •1. Случайность остатков
- •2.Гомоскедастичность дисперсии остатков
- •3.Проверка нормальности частотного распределения остатков
- •Применение гипотеза Хилла для оценки минимально необходимого объема выборки. Клюшин Дмитрий Анатольевич, Доказательная медицина. Применение статистических методов.
- •4 Независимость распределения остатков
- •II. Cтруктурно-параметрический синтез регрессионных моделей
Применение гипотеза Хилла для оценки минимально необходимого объема выборки. Клюшин Дмитрий Анатольевич, Доказательная медицина. Применение статистических методов.
Пусть
 генеральная совокупность СлВел-ы
с неизвестным симметричным распределением
вероятности
генеральная совокупность СлВел-ы
с неизвестным симметричным распределением
вероятности
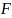 ,
а
R
множество
действительных чисел.
,
а
R
множество
действительных чисел.
Основной
распределеной массой
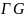 называется подмножество
называется подмножество
 такое, что
такое, что
 , где
, где
 - произвольный элемент выборки, который
получен с помощью случайного отбора
(по рр закону??) из
- произвольный элемент выборки, который
получен с помощью случайного отбора
(по рр закону??) из
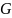 ,
,
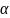 - заданный уровень значимости
(
допустим
- заданный уровень значимости
(
допустим
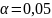 ).
).
Пусть выполнено следующее:
Для получения выборки
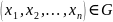 используется
случайный выбор. Обозначим как
используется
случайный выбор. Обозначим как
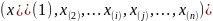 - члены соответствующего выриационного
ряда.
- члены соответствующего выриационного
ряда.
Напомним:
вариационный ряд - это выборка
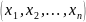 ,
упорядоченая по величине и полученная
последовательность обозначена как
,
упорядоченая по величине и полученная
последовательность обозначена как
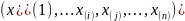
2.Выборочные значения являются реализацией СВ с симметричным абсолютно непрерывным распределением
Тогда выполняется гипотеза Хилла:
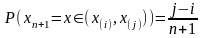 (1)
(1)
(Все доказательства пока опустим)
Теорема 1
Если
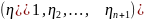 симметрично
зависимые
одинаково
распределенные
случайные
величины с абсолютно
непрерывной функцией распределения
такой, что
симметрично
зависимые
одинаково
распределенные
случайные
величины с абсолютно
непрерывной функцией распределения
такой, что
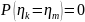 при
при
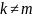 ,
то
,
то
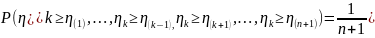
Теорема 2.
Если
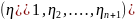 симметрично
зависимые
одинаково
распределенные
случайные
величины с абсолютно
непрерывной
ф-цией распределения такой, что
симметрично
зависимые
одинаково
распределенные
случайные
величины с абсолютно
непрерывной
ф-цией распределения такой, что
при
,
а
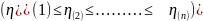 – вариацоный ряд, построенный из первых
n
значений,
то
– вариацоный ряд, построенный из первых
n
значений,
то
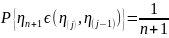
С вяжем
этот результат с
вяжем
этот результат с
уровнем значимости α, как он
введен выше. Уровень значимости
определен так, что 5% точек
попадает в хвосты.
Значит,
считая что хотя бы 1 интервал вариационного
ряда попал какой-то из
2-х хвостов
(это определяет минимальное количество
точек в выборке, что-бы данное событие
произошло) то можно написать что
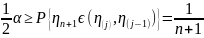 .
Отсюда при заданном α можно записать
.
Отсюда при заданном α можно записать
 и
получить оценку для n:
и
получить оценку для n:
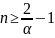
Отсюда
при
α=0,05 имеем
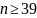
То мы нашли минимальное количество испытаний достаточное для проверки утверждения: если полученные реализации не вышли за пределы +-2сигма - то похожее на нормальное распределение - действительно нормальное
???????Данное утверждение находит связь между значимостью результата (0.05) и минимальным количеством точек, которые нужны для утверждения гипотезы допустим Н0. Условием корректности применения оценки для n есть симметричность и непрерывность рассматриваемых распределений.
Это дает наконец точку опоры для применения теории статичтических гbпотез для относительно небольшиз размеров выборки.
Небольшое отвлечение -
Об условиях применения гипотезы Хилла - напомним
она применима к СВ которые имеют симметричные и абсолютно непрерывные плотности распределения
Ч

 то
такое не
абсолютно непрерывная
функция - это такая непрерывная функция
у которой нет
производной в несчетном количестве
точек.
то
такое не
абсолютно непрерывная
функция - это такая непрерывная функция
у которой нет
производной в несчетном количестве
точек.
рис 33
Канторова лестница - граффик массы канторова стержня от коорд-ы х
канторов стержень - стержень масса которого пропорциональна мощности канторова множества Канторово множество
|
Множества C0, C1, C2, C3, C4, C5, C6 |
C=⋂Сi i=0,...∞ называется Канторовым множеством.
Из единичного отрезка C0=[0,1] удалим среднюю треть, то есть интервал (1/3,2/3). Оставшееся точечное множество обозначим через C1. Множество C1=[0,1/3]∪[2/3,1] состоит из двух отрезков; удалим теперь из каждого отрезка его среднюю треть, и оставшееся множество обозначим через C2. Повторив эту процедуру опять, удаляя средние трети у всех четырёх отрезков, получаем C3. Дальше таким же образом получаем последовательность замкнутых множеств C0⊃C1⊃C2⊃…. Пересечение
СВ с Пл Р как видоизм кантор лестница рис. 33 - будет
непр но не абсолютно непрерывна
