МОДЕЛИРОВАНИЕ по эксп данным (статист моделирование)

Итак мы показали что практ любая зад статистического модедирования является по своей сути задачей оптимизации. Правда в до компьютерную эру безусловный приоритет учених был на стороне аналитич методов моделирования

Вы достаточно много уже знаете о моделировании и это позволяет уже Вам решать несложные маломерные задачи. С другой стороны современный аппарат решения задач построения многомерн регрессии опирается на матричные представления что позволяет увидеть очень ценные свойства аппарата МНК изучить его достоинства и недостатки с тем что-бы грамотно его применять

Поэтому мы еще раз обратимся к постановке задач моделирования и подробно рассмотрим какие практические многомерные задачи возможно решать с помощью МНК , свойства метода, оценок МНК, преимущества и недостатки классических методов многомерного РА и возможные пути решения этих птроблем

Современное моделирование (в том числе аналитическое) принято отслеживать от группы ученых связанных с Ньютоном, создавшего теорию бесконечно малых – Теорию Диференциального и Интегрального исчисления. Это удивительное прозрение практически впервые породило аналит ические математические модели в точности соотв-щие реальным физическим процессам.

Он выдвинул гениальную по простоте и адекватности идею что значительное количество физических моделей макромира увязывают в своих взаимоотношениях линейные перемещения с их скоростями,ускорениями и тд и создал строгий аппарат обращения с данными величинами и уравнениями связвывающими эти величины.

С помощью этого аппарата была решена грандиозная задача - задача моделирования движения тел небесной механики.

Паралельно эта задача породила к жизни сопутствующие направления исследований - теорию вероятности (ЛАГРАНЖ, МУАВР, БАЙЕС).

Конечно ТВ имеет свои родные корни, связанные с изучением случайности, но вычислительные, практические аспекты ТВ стимулировала родственная «небесной механике» задачка из теории измерений. Именно ниже указанная задача стала первой сформулированной задачей статистического моделирования.

Надо было наиболее точно определить начальные условия для реш задачи Неб Мех – то есть определить наиболее точное положение звезд на небосклоне по неоднократным их измерениям..

Таким образом в 1800-тых годах - Лаплас, Гаусс и Лежандр, каждый из которых в то время работал над теорией движения небесных тел и не мог обойти проблемы теории измерений предложили свои варианты решения такой задачи. Сначала о Лапласе.

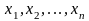Лапласом было предложено оценивать неизвестное значение измеряемой величины по его повторным измерениям как такую величин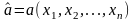у , которая обеспечивает минимум ф-лу (*)

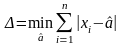Оказалось, что такое значение соответствует нахождению выборочной эмпирической медианы - то есть такому числу 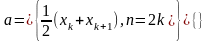, справа и слева от которого находится одинаковое количество измерений.

Позже, было показано что задача минимизации суммы модулей отклонений решаеться линейным программированием. О ЛП?

Но в то время ученому сообществу более простой и технологичной показалась идея двух других французов –Гаусса и Лежандра которые для тех же условий задачи предложили минимизировать ф-нал

(**)

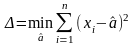и предложили технологию Метода Наименьших Квадратов которую мы в общих чертах уже представляем.

Ниже немного обобщим вгляд на эту технологию моделирования

Задачи моделирования по экпериментальным данным

Исх. данные задачи моделивания - , здесь 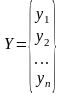– вектор выхода, Х₁,….,Х_m – входы¸ m= кол. перем., n-кол точек данных - матрица значений входных переменных

_{Модель в самом общем виде предпол}агем вида

_{Делаем шаг упрощения задачи – предполагаем наличие в структуре переменных быстрых - х и медленных - а , то есть}

_{и назовем медленые переменые}

_{а – параметрами модели}

При моделировании выделяют две задачи

– параметрический и структурный синтез модели

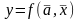
То есть необходимо найти структуру и параметры модели .

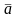Однако на практике применяються несколько другие две задачи:

1.расчета вектора коэфф при заданной структуре модели и

2. более практическая задача, когда ищем и структуру и параметры модели

По поводу различных структур –

Пример – какие ниже стуктуры одинаковые а какие разные

1.У= з-х+х³ 2. у= 3х-х² 3.у= 3+х²+х³ 4. у=3х-х³

При фиксированой структуре эффективность найденных параметров модели оценивают по разному

– один из вариантов - функционалом

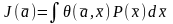или _(*)

где - функция адекватности модели , а - плотность распределения.

С адекватностью понятно –в дискретном случае это может быть “обьясненная дисперсия”, коэфф детерминации (мах) или отн. норм.среднекв.ошибка (мин)

Ну а причем здесь плотность распределения – а?

играет роль весовых коэффициентов в ф-ле, учитывающих частоту попадания объекта в точку i (облaсть i ).

Обычно для построения

-(обращаю внимание на то, что

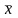_- вектор и - многомерная плотность)

нужно очень много данных,

Когда же мы имеем такую роскошную

возможность иметь столько данных? –

когда имеем длинный сигнал (временной ряд) ,например, в медицинских приборах, и вообще работа в реале с накоплением данных об объекте.

Если наша задача – построить прогнозирующий фильтр (прогнозирующую модель)– тогда для Р(х) учитывают данные всей доступной кривой, а прогнозирующую модель расчитывают используя ограниченный скользящий участок методами стохастической аппроксимации, - то есть взвешивая невязки в соответствие с плотностью.

Когда нет доступа к такому большому количествку данных то

чаще обходятся без , считая в (*), что неизвестна, вернее принимая 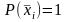, считая все слагаемые равноправными таким образом принимая что плотность равномерна.

Если теперь функционал качества задачи моделирования выбрать в виде суммы квадратичных. невязок

J (а)= _{и при виде моделии}

_{придем к для поиска параметров а к обычному механизму МНК}

Но будем помнить что принцип взвешивания невязок в МНК – важное ответвление РА (называемое взвешенный МНК), и используется он в задачах моделирования при непрерывном поступлении новых данных в систему – это моделироваие сигналов, временных рядов под. которые необходимо подстроить их модели для дальнейшей обработки - например для прогноза ряда, или очистки сигнала от шума и т.д.

Вернемся к обычному МНК

Напомним

Постановку задачи для поиска коэффициентов по методу наименьших квадратов (МНК) при фиксированной структуре модели:

Задана матрица значений аргументов

(**) и вектор выхода ,

1.Введем предположеие – достаточно сильное и тем неприятное - – предположим что модель линейна по параметрам

Предположение вводится в основном потому что мы умеем решать такие задачи, а не потому что это как то обосновано, Здесь есть нечто общее с тем что « будем искать потеряное под.фонарем, потому что там видно а не потому что там потеряли».

₂ Наконец предполагаем что нам известна структура _{то есть сейчас мы занимаемся задачей параметрического синтеза}

Если тепер, как мы говорили выше, функционал качества задачи моделирования выбрать в виде сумм квадратичных. невязок

J(у) = (**)

то для определения вектора параметров достаточно решить систему линейных уравнений 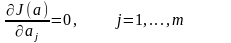(*О*)

Действительно вспомним условия экстремума функций, тогда понятно откуда получена система (*О *)

Обратим внимание что систему получим линейную отностельно а_j

Все достаточно просто.Решая эту систему получаем наилучший вектор парамеров а который дает минимум функционалу (**)

Таким образом решается задача параметрического синтеза.

Для частного случая одномерной регресии У=ах+в, его решение МНК можно получить как простые формулы для , где - коэффициент регрессии, , -коэффициент корреляции х,у,

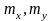и , выборочные среднеквадратические отклонения и выборочные математические ожидания случайных величин и

, , ,

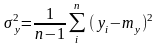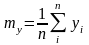
_№2

_{Но если регрессия не одномерная, то никто в наше время в расчетах не записывает функционал в скалярном виде, не берут производные , не составляют системы скалярных уравнений и тд. Для решения задачи поиска параметров регрессии пользуются матричные представления данных и операций. Я пользовался выше скалярной записью, только затем, что-бы в начале было проще показать смысл процедур поиска параметров.}

У прощенный вывод формулы МНК в матричном виде

Напомним

1.– Для умножения матриц А и В – А*В=С

–то есть получения элемента необходимо взять в А (первой матрице) j-тую строку 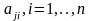и в В (второй матрице) k-тый столбец и образовать скаляное поизведение .

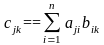2 . Траспонирование

– столбцы делает строками, строки столбцами

(в квадратной матрице – просто зеркально отображаем относительно гл диагонали)

3.Обратная матрица А^-1 матрицы А это такая матрица для которой выполняется А^-1 _*А=Е, где единичная матрица

Итак имеем матрицу Х и вектор выхода У

н еобходимо построить модель линейной структуры

Уже понимаем почему пишем Ха а не аХ

П ри этом необходимо максимально приблизить с помощью вектора а матричное соотношение (***)

В скалярном виде это соответствует наилучшему приближению

_{в первой точке}

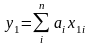
………… в n-ой точке - (***)

Д алее будем исходить из (***) как из равенства и будем из него искать а. Более обосновано вывод проведем немного позже. Итак имеем

Для того что-бы освободить а (умножить то что при а на обратную Х матрицу и получить в результате Е – ед матрицу ) надо чтобы при а стояла квадратная матрица.

Умножим слева и справа на Х^Т получим Теперь поскольку Х^ТХ – квадратная – можем ее умножить на обратную -

слева и справа на (Х Х^Т)^-1

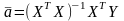
и окончательно имеем для а

и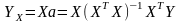 для модели

Все - И все расчеты проводятся по этой формуле

- в любых инжененых пакетах реализованы матричные операции -

все очень просто (мы поработаем на практике) и

не очень просто в связи с операцией взятия обратной матрицы и понятием плохой обусловленности матрицы.

Что это - плохая обусловленность матрицы:

напомним о так наз. собственных числах матрицы

/А-лЕ/=0 ......для опред Л - решаем степенное уравнение соответствующего порядка напомним на примере 2-го порядка

ПлОбМа возникает когда λmin << λmax.

и численно мера ПОМ выражается их отношением

или близостью к нулю ее детерминанта -

Этот эффект ПОМ обычно набл когда в А одновременно присутствуют очень большие и очень малые числа - тогда при операции нахождения обратной матрицы обусловленность резко ухудшается (очень малые числа деляться на очень большие) и лавинообразно растет погрешность (изза выхода значущих цифр за пределы разрядной сетки ВМ)- решение теряется в эффекте ПлОбМа

Это одна из причин что РА только начинается а не заканчивается на формуле для а. Преодоление ПОМ - различные алгоритмы регуляризации матрицы А ......желательно с минимальной потерей ее эквивалентности

Другие проблемы больше связаны с задачей структурного синтеза - об этом позже А пока более строгий вывод, который

повторяет логику, изложенную для скалярного вида:

Пусть размерность задачи m переменных и n точек

Критерий по которому работает МНК: минимировать сумму квадратов ошибок е_i =У_i-(а_о+а₁х_1i+…+а_mx_mi ) модели У=а_о+а₁х₁+…+а_mx_m в заданных точках. В матричном виде, модель У=Ха должна минимизировать критерий в матричной форме:

_{Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матр. форме)}

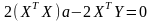, отсюда (** ) и далее решая (**) можем найти вектор а=(х^тх)^-1х^ту

В расшифрованном матричном виде эта система уравнений имеет вид

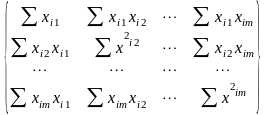
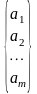₌ X и X^TX - осн

_{Где все суммы берутся по количеству точек}

_{Если в модель включен свободный член то 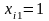для всех 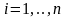i}

Это и есть т.н. нормальная система уравнений

Решение этой системы и дает общую формулу МНК-оценок

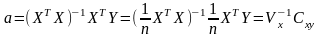
_X и X^TX - основные золотые матр мод -матрица объект-свойства и информационная матрица Фишера (при центр Х - ковар матрица)

_{И так с расчетов параметров на первый взгляд все просто (на самом деле проблема есть с обращением матриц,)}

А вот со структурно-параметрическим синтезом так просто не получается

Для понимания в каких условиях и почему классические шаговые алгоритмы многомерной регрессии, к сожалению, не дают ожидаемых наилучших результатов моделирования при структурно-парам. Синтезе. Нам полезно

1. рассмотреть геометрические интерпретации МНК и

2. привести некоторые свойства метода МНК и регрессионных моделей

1 что такое обусл М 2 почему она плоха

Геометрические интерпретации МНК или почему регрессия не алгебра (более корректно -почему регрессионные. уравнения не алгебраические уравнения).Детский вопрос –

если в алгебре из

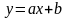
то почему в регрессионных уравнениях из ,

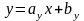не следует что 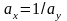и ?

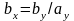А имеем мы (у вас эти ф-лы есть)

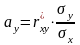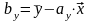, и

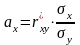
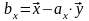где 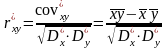- выборочный коэффициент корреляции

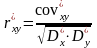( - оцен зн. коэфф корр. ур совпадут при одинаковом расбросе - это так потому что просто первая формула представит график в осях у-х а вторая х-у )

Для того что бы не формально понять эти результаты (и для других целей) полезны геометрические интерпретации регрессии.

…………..

Напомним, что нам известно

Любая задача моделированмя по экспериментальным данным начинается с данных – таблицы результатов эксперимента или таблицы наблюдений –

здесь m= кол.перем., n-кол точек данных

Итак, матрица данных имеет m столбцов и n строк, соответственно

геометрическую интерпретацию регресии можно получить

в пространстве столбцов или

в пространстве строк

= или что то же самое

в пространстве переменных (оси –переменные) или

в пространстве точек. (оси - номера точек)

Интерпретация в пространстве переменных (столбцов)

Рассмотрим случай одномерной регрессии – имеем только столбцы У и Х₁

Идея регрессии пришла в математику из теории вероятности. ТВ по сути дала следующее

определение понятию регресии у по х: регрессия у по х это матожидание СВ У с условной функцией распределение вероятности 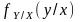: 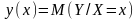(1)

или с учетом,что у нас есть только конечная выборка 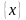, то 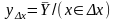( 2) Теоретически при увеличении выборки ( 2) (1), то есть ,

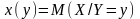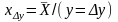аналогично регрессия х по у это матожидание СВ Х с условной функцией распределение вероятности : - с учетом конечности выборки ( 2*)

Тогда использовав выборочные оценки мат. ожиданий как формулы для средних значений точек попавших в полосы и получим приближенные выражения для геометрического построения регрессий

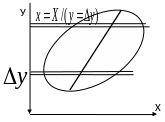
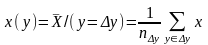
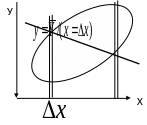
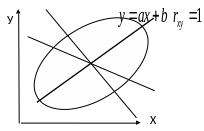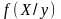Е сли условные распределения и унимодальны и симметричны то по этим формулам для средних линий в полосах получим в каждом “яйце” точки, принадлежащие линии регрессии. Для каждой линии достаточно построить по 2 точки и мы их проведем. Обращаю внимание что регрессии у=f(x) и х=f(у) не совпадают ?Они совпадут (центр. линия) – и регр превр в алгебру-когда рассеян симм отн бисктр и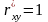

Интерпретация в пространстве точек

Интерпретируем на осях двух точек

и для 2-х векторов - У и Х₁

(хотя при осях 2 точек можно и все вектора

изобразить )

Для простоты будем изображать

центрированные варианты векторов

(без своб.члена)

Отложим в пространстве осей 2-х точек (две оси, чтобы возможно. было изобразить геометрическую интепретацию) вектора у и х

Регрессия МНК это проекция

моделируемого вектора в

плоскость векторов, по которым

моделируем.

А в одномерном случае

- это проекция на тот вектор,

с помощью которого мы

мы моделируем . То есть -

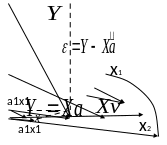
Проектируем вектор у на вектор х и получаем модель у по х:

у_х =а_хх

Проектируем вектор х на вектор у и получаем модель х по у: х_у =а_уу

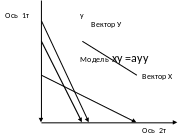
Или на одном рисунке -

Теперь понятно, - поскольку проекции у_х и х_у – не совпадают, то и уравнения у них разные - из одной модели другая не получится.

А совпадут они - при колинеарности у и х

(что есть геометрический эквивалент коррелируемости )

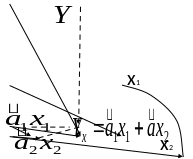Регрессия МНК это проекция моделируемого вектора в плоскость векторов, по которым моделируем ----------в плоск 2-х иксов

2 ?? === ===========================

Свойство проективности МНК

( вывод осн ф-ла МНК, используя теперь свойство проективности)

1. Напомним, что применяя МНК для регресии (1)

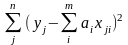мы оцениваем параметры регресии с точки зрения минимизации функционала : = (1*)

Здесь 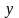и наблюдаемые и модельные значения соответственно.

Напомним что дальнейшие результаты будут такие же, если мы вместо (1) будем рассматривать модель более общую модель 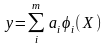(2) и ф-нал = 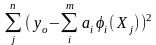(2*)

Результаты будут верны с точностью до переобозначения.

Поэтому, рассуждая в дальнейшем об (1) что формально проще, имеем далее в виду и (2) то есть модель нелинейную по аргументам регрессии.

2. Описывая данные задачи регрессии в виде таблиц естественно и выводить основные результаты в матричном виде (что бы не выделять отдельно своб член - ниже для упрощения записи - - ед.вектор) поэтому введем обозначения:

вектор 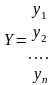матрица и вектор

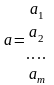
Напомним осн. правила матричных операций

1.– Умножения – А*В=С - то есть для получениия jk-того элемента С - в А берут j-тую строку, в В k-тый столбец и их скалярно перемножают.

2 . Траспонирование

– столбцы делает строками, строки столбцами

(в квадратной матрице – просто зеркально

отображаем относительно гл диагонали)

кроме того: (АВ)^Т=В^Т А^Т и следствие (АВС)^Т=С^ТВ^ТА^Т

3.Обратная матрица А^-1 матрицы А это такая матрицадля которой выполняется

А^-1 _*А=Е, где единичная матрица

4.Свойство ортогональности векторов а и в:

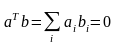
Н аше требование к регресии - выполнение равенств - что должно бы выполняться - в первой точке

………… в n-ой точке - (*)

На самом деле выполнить их невозможно ввиду предположения

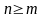
Эти условия (требования) (*) в матричном виде можно записать как

(именно в таком порядке =операция умножения – срока Х на столбец а)

Для решения задачи регрессии среди всех моделей нужно выбрать ту которая удовлетворяет условиям (*) наилучшим образом в смысле функционала (1)

Матричную запись модели можно представить как уже выполн. условие 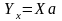(вместо ) с найденными оценками .

То есть в результате решения мы находим такие которые формируют наилучшим образом приближая условие

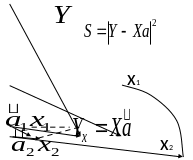Приближение это реализуется МНК как проектирующий механизм. Покажем это

Если выражение, которое нам надо приблизить в матричном виде выглядит как

т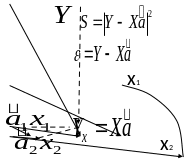 о естественно что матричный аналог квадратичной невязки (1) –это . Эта ошибка есть расстояние от вектора  до вектора  .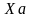

Вектор  должен лежать в пространстве переменных (столбцов) матрицы 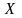 , так как  есть линейная комбинация столбцов этой матрицы с коэфф.  .

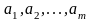Отыскание решения  по методу наименьших квадратов эквивалентно задаче отыскания такой точки (вектора)

 

которая лежит ближе всего к  и находится при этом в пространстве столбцов матрицы  .

Таким образом, вектор 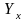 должен быть проекцией  на пространство столбцов и вектор невязки  должен быть ортогонален этому пространству.

Далее для упощения записи вывода формулы МНК отрбросим значки “тильда”

Ортоганальность вектора невязки пространству можно определить след образом:

Л

юбой (произвольный) вектор в пространстве столбцов есть обязательно линейная комбинация столбцов с некоторыми коэффициентами 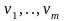 , то есть это вектор  .

При произвольном 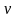вектор - это любой произвольный вектор, который можно положить в гиперплоскость построенную на векторах .

Для всех  в пространстве , эти вектора должны быть перпендикулярны невязке  , в силу этого – условие отрогональности:

Так как это равенство должно быть справедливо для произвольного вектора  , то (*)

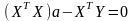Таким образом мы нашли сооошение дающее решение по МНК несовместной системы условных уравнений 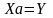, состоящей из n уравнений с m неизвестными (*)

которая называется системой нормальных уравнений

Если столбцы матрицы  линейно независимы????, то матрица  обратима и можем получить решение для - одна их причин треб незав Х - и чем ближе к ЛЗ будут вектора тем хуже обусловлена

(**)

Правда, естественно, решение не в том смысле, что оно превращает его в равенство, а в том, что в пространстве находит ближайший к нему вектор - проекцию . Вот для него имеем равенство

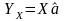
Что и есть решение – основная народнохозяйственная ф-ла МНК

(брать производн. ф-ла,, приравн его=0, решать систему– проверте на примерах).То есть машина производных не берет а реалмзует полученную матричную формлу различными вычисдтельными процедурами. Самое слабое место – обращение матрицы, особенно при ее плохой обусловленности (корр переменных) – это будет у нас отдельный разговор.

*2 ====== Оператор проектирования. Свойства оператора.

Полученный результат имеет полезное для приложений свойство –

Из выражение получаем формулу оператора проектирования вектора в плоскость :

Проекция вектора  на пространство столбцов матрицы имеет вид (подставляя значение из (**))

Матрица 

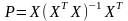
называется матрицей проектирования вектора  на пространство столбцов матрицы  .

Посмотрите какой интересный вид у нее.

Эта матрица имеет два основных свойства:

1. она идемпотентна 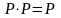, и

2. она симметрична - .

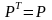Проверим

1.

2.по 2 = =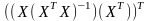 = =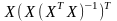 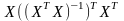Или более просто по 3- центральную скобку не трогаем при перестановке, края меняем местами и транспонируем, ценр тоже транспонируем

= =

Очень важно что верно и обратное: матрица Р, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов Х произвольного вектора У.

Данные свойства могут использоватся при проверке корректности использования МНК (в первую очередь зашумленность данных)

- потеря указанных свойств матрицей Р служит сигналом что оценки МНК (в силу нарушения условий применения - о них ниже ) потеряли свое качество – Состоятельность , несмещеность и эффективность

Именно эти наруш єтих св - вызывают необходимость корректировки расчета, отыскания новых регрессоров, фильтрации шумов, расчета нескольких уравнений регресии вместо одного и т.д. о чем вам расказывал ЕА

Все это делается для минимизации минимизации последствий нарушения условий применения МНК (а они, как увидим нарушаются практически всегда).

Рассмотрим указанные выше свойства, нарушения которых делает применение МНК неэффективным.

??7 к 2=================

3=========

Свойства оценок регрессионных моделей

Наромним самую простую, первую постановку МНК из из теории измерений Теории Вероятности ( в связи с разработкой теории измерений)

в 1800-тых годах .Авторы - Лаплас, Гауссом и Лежандр, каждый из которых в то время работал над теорией движения небесных тел и не мог обойти проблемы теории измерений.

Лапласом

было предложено оценивать неизвестное значение измеряемой величины по его повторным измерениям как такую величину , которая обеспечивает мин. ф-лу

(*)

Оказалось, что такое значение соответствует нахождению выборочной эмпирической медианы - то есть такому числу , справа и слева от которого находится одинаковое количество измерений.

Позже, было показано что задача минимизации суммы модулей отклонений решаеться линейным программированием. О ЛП?

Но в то время ученому сообществу более простой и технологичной показалась идея двух других французов –Гаусса и Лежандра которые для тех же условий задачи предложили минимизировать ф-нал

(**)

и предложили технологию Метода Наименьших Квадратов.

Какие же предусловия применения МНК? что надо

Доказано что выполнении условий

1.Каждое измерение есть реализация случайных величин-

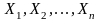
2. Случайные величины - независимы

3.Случайные величины - одинаково распределены с

3.1. одинаковыми МО 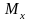и

3.2 одинаковыми постоянными дисперсиями 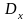(гомоскедактичность)

то оценка полученная по МНК будет

состоятельна, несмещена и эффективна

После выполнения расчета по МНК проверка корректности

можно переформулировать для остатков 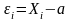решения по МНК («постусловия» применения МНК):

1) величина я вляется случайной переменной распределенной по нормальному закону;

2) математическое ожидание равно нулю: ;

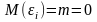3) дисперсия постоянна: для всех i;

4) значения независимы между собой, следовательно, справедливо

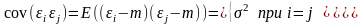
Поэтому если не было уверенности в том что условия применения МНК выдержаны – после решения обязательно проверяют свойства остатков

Если условия применения МНК были соблюдены то выполняются следующие свойства оценок параметров модели;

1. Состоятельность оценки –

Оценка 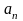числового параметра , определенная при n= 1, 2, … называется состоятельной, если она сходится по вероятности к значению оцениваемого параметра при безграничном возрастании n объема выборки. Или иначе: Статистика является состоятельной оценкой параметра тогда и только тогда, когда для любого положительного числа ε справедливо предельное соотношение

(*)

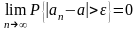Заметим, что такое определение - более слабое чем

и это дань тому, что определяется не рекурентнтно, например, а через реализации случайных величин . Примеры

Выборочное среднее

и выборочная. медиана

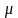
и выбор. дисперсия

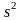
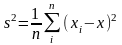
по вероятности сходятся соответственно к

МО 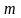, медиане и дисперсии 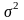и поэтому это

– состоятельные оценки параметров случайной величины Х

2. Несмещенность оценки

Несмещенная оценка – это оценка параметра , математическое ожидание которой равно значению оцениваемого параметра:

Наиболее характерным примером смещенности оценки есть выборочная дисперсия

– как мы говорили – это состоятельная оценка но оказывается – смещенная !. Можно показать что 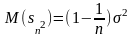отличается от на кусочек

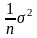
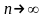
Но при 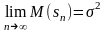так как

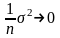
Такую несмещенность называют асимптотической несмещенностью.

А для дисперсии - состоятельной и несмещенной оценкой оказывается выборочная статистика

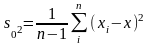
именно для нее имеем

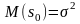
3. Эффективность оценки

Эффективная оценка – это несмещенная оценка, имеющая наименьшую дисперсию из всех возможных несмещенных оценок данного параметра

Доказано, напимер что  и  являются эффективными оценками параметров m и σ² нормального распределения.

Что же получиться при нарушении всех или части из 1- 4 – свойств? –нарушаются перечисленные выше свойства (в разной мере)

Если оценка не состоятельна это значит что мы ее не только неточно определяем, но вообще не то расчитываеим, а что расчитываем надо отдельно разбиратьься

Если оценка смещена – то хорошо если только ассимтотически смещена. А если просто смещена надо постаратся разобратся в оценке смещения

Наконец если оценка неэффективна – надо искать лучшую, эффективную.

3 =========================

Анализ остатков решения МНК

Одним из распространенных приемов оценки условий применения МНК – это анализ остатков моделирования.

И так есть табличные значения выхода 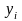, выхода модели и остатки моделирования ,

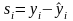Основные свойства проверяемые при анализе -

- случайность остатков (равномерность распределения вдоль оси аргументов)

-гомоскедатичность дисперсии остатков

- нормальность частотного распределения остатков с нулевым МО

- независимость остатков

1. Случайность остатков

Свойства проверяются путем анализа графиков остатков вдоль оси аргументов.

С этой целью стоится график зависимости остатков e_i от известных модельных значений выхода.

Если на графике получена горизонтальная

полоса, то остатки представляют собой

случайные величины от найденной модели

и был МНК оправдан, значения   

хорошо

аппроксимируют фактические значения y.

Возможны следующие случаи, если  зависит от  то:

- Разброс (дисперсия) постоянна,

МО –переменно и не равно 0.

- Дисперсия остатков переменна –

гетероскедатична (в этом случае

остатки тоже неслучайны)

- остатки носят систематический

характер

- Свойства оценок параметров регрессии (несмещенность) нарушается и в случае зависимости случайных остатков от входных аргументов x, Поэтому необходим анализ

графиков остатков от факторов x_j,

вошедших в уравнение регрессии:

есть ли там зависимость

или нет нам зависимости?

По поводу анализа графиков от x_j,

- повторяем все то же что при анализе от выхода у_j

Добавим что: Скопление точек в определенных участках значений фактора x_j говорит о наличии систематической погрешности модели.

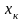 Во всех этих случаях необходимо либо менять базис расчета регрессии - функции , либо вводить новую информацию – допонительные признаки и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами