Силы в механике

Закон всемирного тяготения

,

где F - сила взаимного притяжения двух материальных точек; m₁ и m₂ - их массы; r - расстояние между точками; G - гравитационная постоянная.

В написанной форме закон всемирного тяготения можно применять и к взаимодействию шаров, масса которых распределена сферически-симметрично. В этом случае r есть расстояние между центрами масс шаров.

Напряженность гравитационного поля

,

где F - сила тяготения, действующая на материальную точку массы m, помещенную в некоторую точку поля.

Напряженность гравитационного поля, создаваемого планетой, массу М которой можно считать распределенной сферически-симметрично

,

где r - расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.

Ускорение свободного падения на высоте h над поверхностью Земли

,

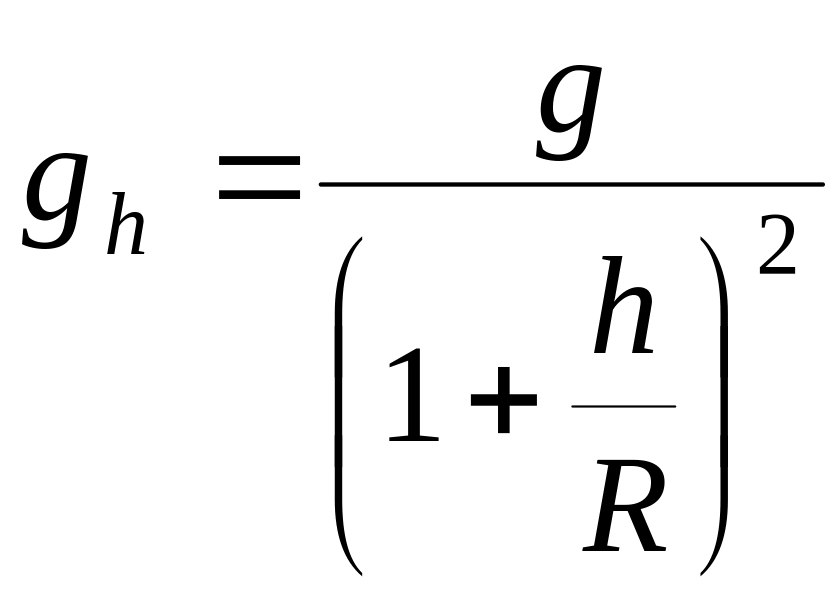где R - радиус Земли; g - ускорение свободного падения на поверхности Земли. Если , то

.

Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m₁ и m₂ (шаров с массой, распределенной сферически симметрично), находящихся на расстоянии r друг от друга

(Потенциальная энергия бесконечно удаленных друг от друга материальных точек принята равной нулю.)

Относительная деформация при продольном растяжении или сжатии тела

,

где ε - относительное удлинение (сжатие); x – абсолютное удлинение; l – начальная длина тела.

Напряжение нормальное

,

где F_ynp - упругая сила, перпендикулярная поперечному сечению; S - площадь этого сечения.

Закон Гука для продольного растяжения или сжатия

, или ,

где k - коэффициент упругости (в случае пружины - жесткость); Е – модуль Юнга.

Потенциальная энергия растянутого или сжатого стержня

, или ,

где V - объем тела.

5. Релятивистская механика

В специальной теории относительности рассматриваются только инерциальные системы отсчета. Во всех задачах считается, что оси у, у' и z, z' сонаправлены, а относительная скорость v₀ системы координат К' относительно системы К направлена вдоль общей оси хх'.

Релятивистское (лоренцево) сокращение длины стержня

,

где l₀ - длина стержня в системе координат К', относительно которой стержень покоится (собственная длина); l - длина стержня, измеренная в системе К, относительно которой он движется со скоростью v; с - скорость распространения электромагнитного излучения.

Релятивистское замедление хода часов

,

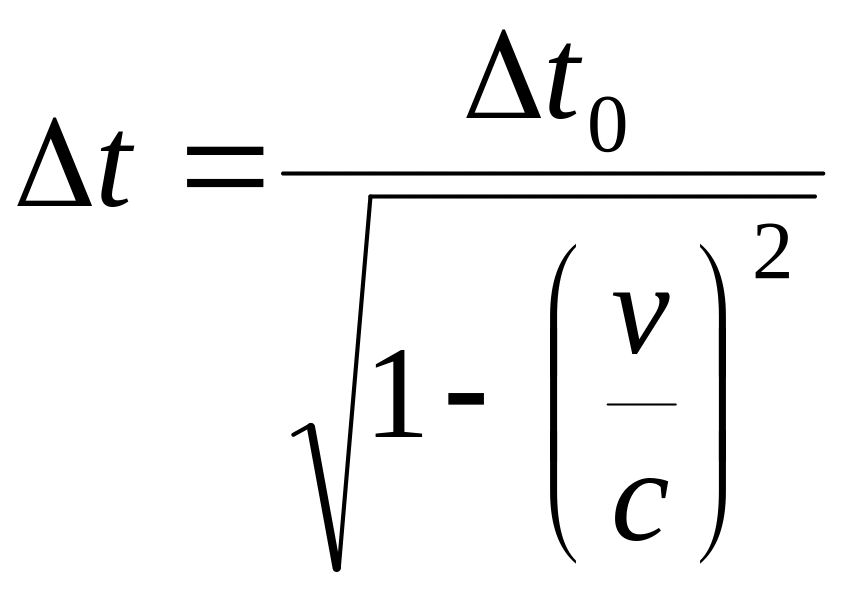где Δt₀ - интервал времени между двумя событиями, происходящими в одной точке системы K', измеренный по часам этой системы (собственное время движущихся часов); Δt - интервал времени между двумя событиями, измеренный по часам системы K.

Релятивистское сложение скоростей

,

где v' - относительная скорость (скорость тела относительно системы K'); v₀ - переносная скорость (скорость системы K' относи­тельно К), v - абсолютная скорость (скорость относительно системы К).

В теории относительности абсолютной скоростью называется скорость тела в системе координат, условно принятой за неподвижную.

Релятивистская масса

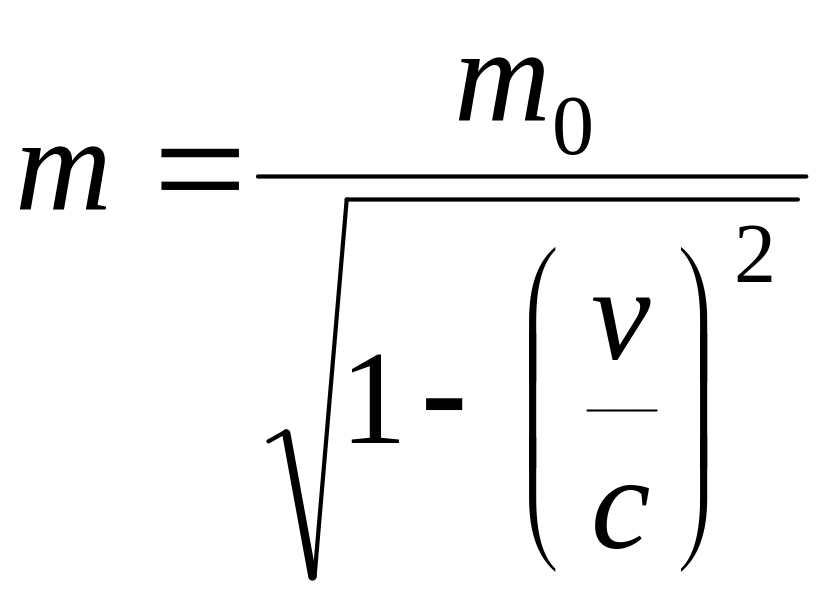, или ,

где m₀ - масса покоя; β - скорость частицы, выраженная в долях скорости света ( ).

Релятивистский импульс

, или ,

Полная энергия релятивистской частицы

,

где - кинетическая энергия частицы; - ее энергия покоя.

Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если v<<с.

Связь полной энергии с импульсом релятивистской частицы

Связь кинетической энергии с импульсом релятивистской частицы