Отношение сравнимости целых чисел по модулю.

Определение 1.

–фиксированное число.

Числа x и y называются равными по модулю m (обозначается ), еслиделится без остатка наm.

Пример.

Замечание.

x делится на m.

При m = 1 отношение становится универсальным, т. е. любые два x и y .

Теорема 1.

Отношение сравнимости по модулю m является эквивалентностью на Z.



Теорема 2.

имеют одинаковый остаток при делении на m.



Разделим числа x и y на m с остатком.

Разделим числа x и y на m с остатком.



Следствие.

Каждый класс эквивалентности по отношению сравнимости по модулю m состоят из целых чисел, имеющих одинаковый остаток при делении на m имеется ровноm классов эквивалентности, соответствующих остаткам .

Определение 2.

Рассмотрим

называется вычетом x по модулю m.

Если , тоy называется наименьшим неотрицательным вычетом числа x по модулю m.

Определение 3.

На множестве (и наZ) определены операции сложения и умножения по модулю m (обозначение ) –остатки от деления суммы и произведенияx и у на m.

Пример.

	0	1
0	0	1
1	1	0

	0	1
0	0	0
1	0	1

	0	1	2
0	0	1	2
1	1	2	0
2	2	0	1

	0	1	2
0	0	0	0
1	0	1	2
2	0	2	1

Лекция № 5. Отношение сравнимости целых чисел по модулю. (продолжение)

Пример.

Теорема 1.

Пусть , тогда:

1. 

2. 

3. 



1)

2)

3)



Замечание.

Если , то, но если, то отсюда не следует, а следует, что.

Теорема 2.

Линейное уравнение с одним неизвестным.

Обозначение.

(1)

заданы

Пусть .

Теорема 1.

Пусть .

1. Если число не делится на, то уравнение (1) не имеет решений.

2. Если , то уравнение (1) имеет ровнорешений в.



1. Следует из свойств сравнений.

2. Рассмотрим два случая:

   1. 

Рассмотрим функцию . Покажем, чтоявляется биекцией.

Инъективность: Пусть . Допустим, что, т. е.делится наm, НОД

Если , то, т. е.является инъекцией.

На различных значенияхфункцияпринимает различныезначений из множествасюръективна.

Таким образом биекция, т. е.имеет единственное решение.

2. 

По результатам пункта I уравнение имеет единственное решение в множестве ,

тогда являются решениями уравненияв .



Пример.

1.

2.

Линейные диофантовы уравнения.

Обозначение.

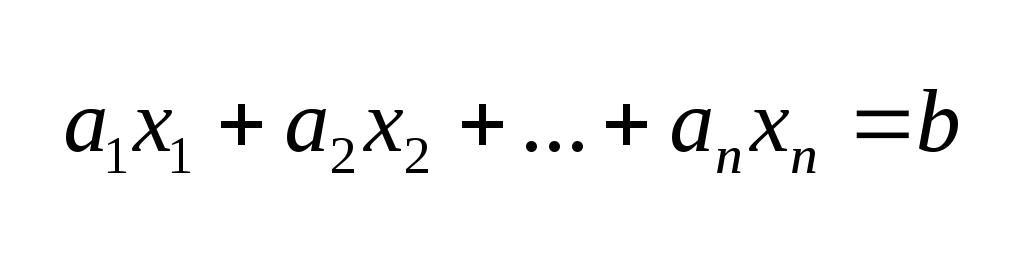(2)

заданы

Теорема 1.

Рассмотрим уравнение , если, то уравнение не имеет решений, если, то.

Теорема 2.

Рассмотрим уравнение . Пусть. Если, то решений нет, если, тоa, b, c делятся на d и можно сократить уравнение на d. В дальнейшем будем предполагать, что a и b взаимно простые, т. е. .

Обозначение.

(3)

Теорема 3.

Пусть . Если, то уравнение (3) решений не имеет, иначе (3) имеет бесконечно много решений:



1. –решение уравнения очевидно.

2. 

Пусть – любое решение уравнения (4), т. е., т. е..



Пример.