Лекции по линейной алгебре и аналитической геометрии

3 Семестр

Лектор Мещанинов Дмитрий Германович

Лекция № 1. Множества и операции над ними.

Обозначение.

A,B,C… – множества

a,b,c… – элементы множества

Определение 1.

Функция принадлежности множества А

Определение 2.

Универсальное множество

Определение 3.

Пустое множество

Операции над множествами:

1. Пересечение

2. Объединение

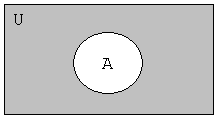
3. Дополнение

4. Разность

5. Симметрическая разность

Определение 4.

Отношение включения множеств

Определение 5.

Пример.

1. 

2. 

3. 

Свойства включения:

1. Принцип равенства

2. 

3. Рефлективность

4. Транзитивность

5. 

6. 

Обозначение.

Свойства пересечения, объединения и дополнения

(законы булевой алгебры):

1. Идемпотентность

2. Коммутативность

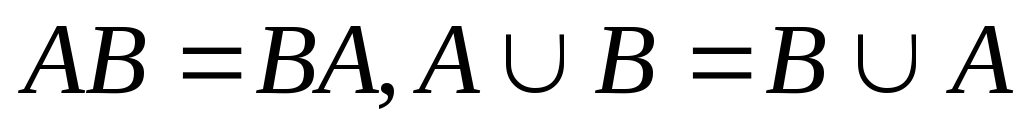
3. Ассоциативность

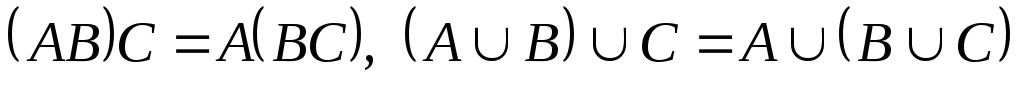
4. Поглощение

5. Модулярность

6. Дистрибутивность

7. 

8. 

9. Инволюция

10. Закон де Моргана

Свойства разности и симметрической разности:

1. 

2. 

3. Коммутативность

4. Ассоциативность

5. Дистрибутивность

Теорема 1.

Множество из n элементов имеет число подмножеств .

Докажем, используя метод математической индукции.

Базис индукции

Индуктивный переход

Рассмотрим все подмножества А и разобьем их на 2 части:

1. Не содержащие , т. е. все подмножества

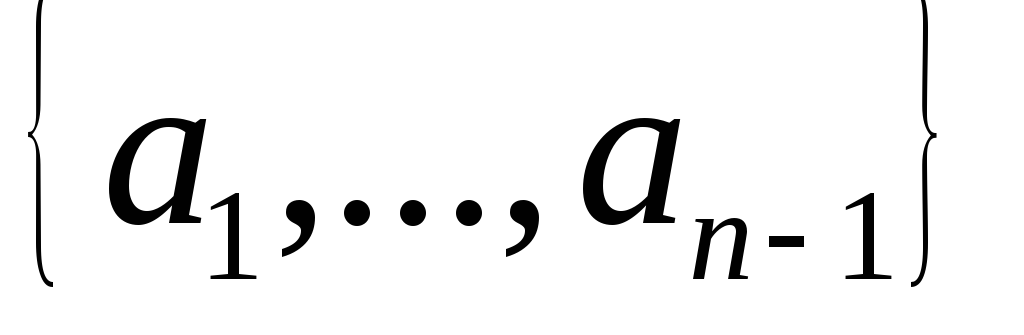
По индуктивному предположению их ровно

2. Содержащие , их тоже.



Пример.

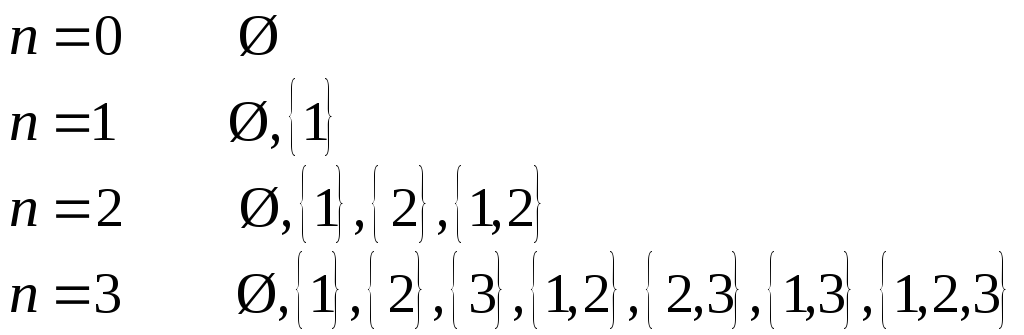
Определение 6.

Декартово произведение .

Пример.

Свойства декартова произведения:

1. 

2. 

3. Если множества А и В конечны и состоят из n и m элементов, то их декартово произведение также конечно и состоит изmn элементов.

Отношения.

Определение 1.

Пусть – некоторые множества.

n-арные (n-мерные) отношения (свойства) на множествах – это подмножества

n=1 – унарное свойство

n=2 – бинарное свойство

n=3 – тэнарное свойство

Пример.

1. Унарное отношение «быть чётным числом» на Z.

2. Бинарное отношение

3. Тэнарное отношение

Теорема 1.

Если – конечные множества, состоящие изэлементов, то на этих множествах можно задать число различныхn-арных отношений .

Способы задания отношений:

1. Словесное описание на каком-либо языке.

2. Таблицами, списком элементов.

Бинарные отношения:

3. Инфиксная запись символа отношения

4. Графиком

5. Матрицами из 0 и 1

6. Ориентированным графиком

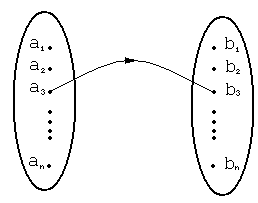
Определение 2.

–однородные бинарные отношения на множестве А.

Пример.

График

Матрица

Ориентированный график

Лекция № 3. Соответствия и функции.

Определение 1.

Пусть является функцией.

Определение 2.

Функция (отображение) называется инъективной (инъекцией), если разные элементы множества А имеют различные образы.

Определение 3.

Функция (отображение) называется сюръективной (сюръекцией), если множество А совпадает со всем множеством В.

Определение 4.

Функция (отображение), инъективная и сюръективная одновременно, называется биективной (биекцией) (взаимно однозначное соответствие).

Замечание.

Интерпретация этих свойств на графах.

Функция – из каждой вершины множества А выходит не более одной стрелки.

Отображение – каждой вершины множества А выходит ровно одна стрелка.

Инъективная функция – в каждую вершину множества В входит не более одной стрелки.

Сюръективная функция – в каждую вершину множества В входит не менее одной стрелки.

Примеры.

Не функция

Функция, но не отображение

Инъекция, но не сюръекци

Функция не инъективная и не сюръективная

Сюръекция, но не инъекция

Биективная функция, не биекция

Замечание.

Отображение является биекцией

Теорема 1.

Пусть А и В – конечные множества из m и n элементов, тогда

Теорема 2.

Пусть А и В множества из m и n элементов и , тогда существует ровно:

1. различных соответствий;

2. различных функций;

3. различных отображений;

4. различных инъекций;

5. различных биекций.



1) Следует из теоремы о числе различных n-арных отношений.

2)

–любой из n элементов Øразличных функций.

3) различных отображений.

4)

инъекций.

5) Следует из (4) при n=m. 

Теорема 3.

Пусть иявляются биекциями, тогда:

1) Существуют обратные функции и, которые тоже являются биекциями.

2) Их композиция тоже является биекцией.



1)

2)

