
Ответы на экзаменационные билеты_2
.doc-
Матрицы. Операции сложения матриц и умножения матриц на число. Транспонирование матриц. Операция умножения матриц и её свойства.
Определение.
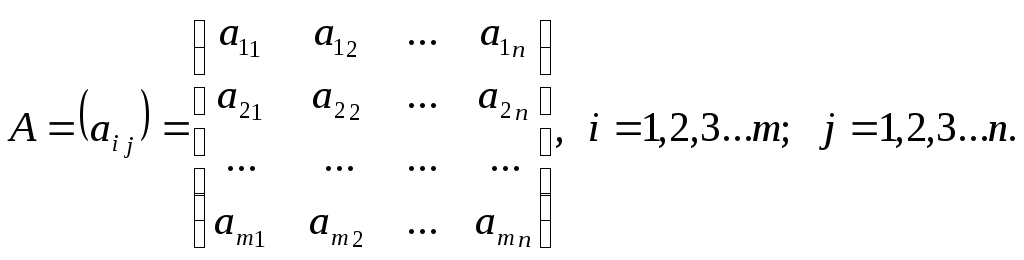
Матрицей размера
mxn
называется прямоугольная таблица чисел,
состоящая из m
строк и n
столбцов. А числа
![]() называются элементами матрицы А.
называются элементами матрицы А.
Операции над матрицами.
-
Сложение матриц
![]()
Свойства:
![]()
![]()
![]()
![]()
-
Умножение матрицы на число
![]()
Свойства:
![]()
![]()
![]()
![]()
-
Умножение матриц
![]()
Свойства:
![]()
![]()
![]()
-
Транспонирование матриц
![]()
Свойства:
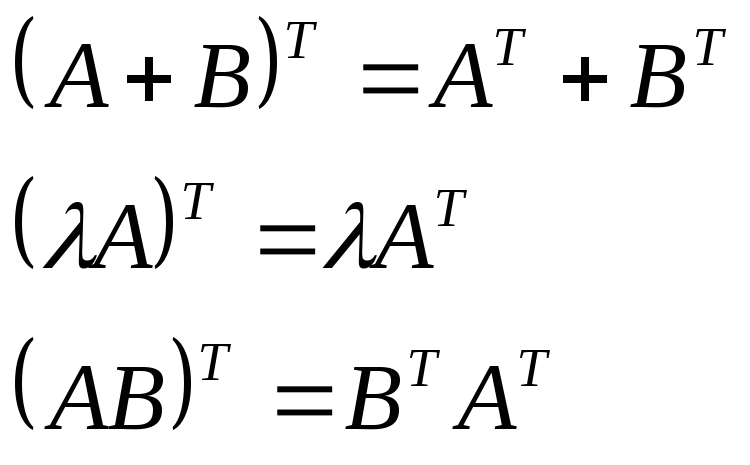
Виды матриц.
-
 – матрица-строка
(столбец);
– матрица-строка
(столбец); -
 – квадратная
матрица;
– квадратная
матрица; -
 – симметрическая
матрица;
– симметрическая
матрица; -
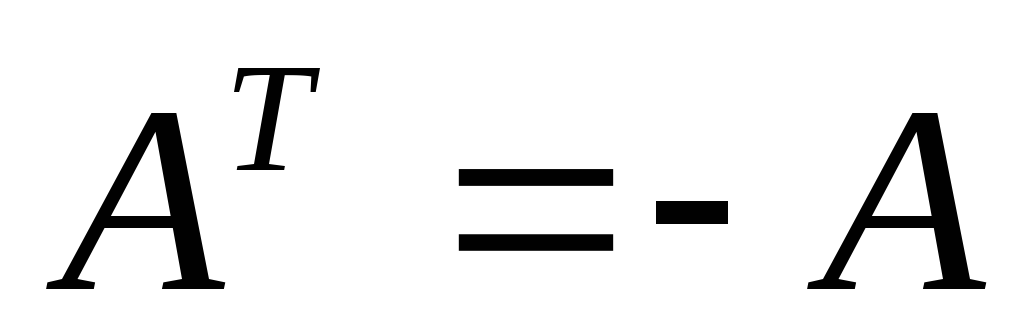 – кососимметричная
матрица;
– кососимметричная
матрица; -
 – нулевая матрица;
– нулевая матрица; -
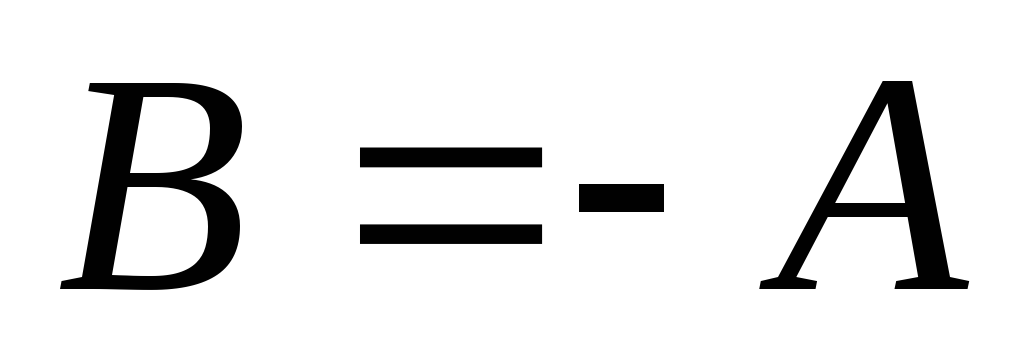 – противоположная
матрица;
– противоположная
матрица; -
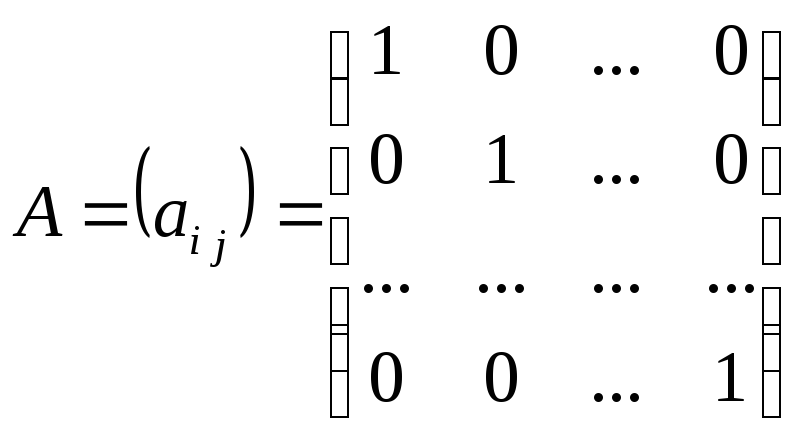 – единичная
матрица.
– единичная
матрица.
-
Перестановки и подстановки, их свойства.
Определение.
Всякое расположение
чисел
![]() в некотором определённом порядке
называется перестановкой из n
чисел (символов). Общий вид перестановки
в некотором определённом порядке
называется перестановкой из n
чисел (символов). Общий вид перестановки
![]() .
.
Всякое взаимно
однозначное отображение A
множества первых n
натуральных чисел на себя называется
подстановкой. Общий вид подстановки
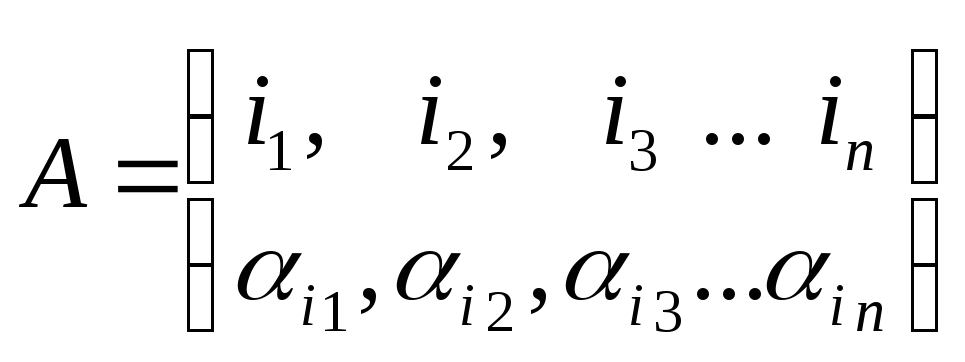 .
.
Свойства перестановок и подстановок.
-
Число различных перестановок из n символов равно n!
-
Все n! перестановок из n символов можно расположить в таком порядке, что каждая следующая будет получаться из предыдущей одной транспозицией, причём начинать можно с любой перестановки.
-
Всякая транспозиция меняет чётность перестановки.
-
При
 число чётных перестановок из n
символов равно числу нечётных, т.е.
число чётных перестановок из n
символов равно числу нечётных, т.е.
 n!
n! -
Число подстановок n-й степени равно числу перестановок из n символов, т. е. равно n!
-
Число чётных подстановок n-й степени равно числу нечётных, т.е.
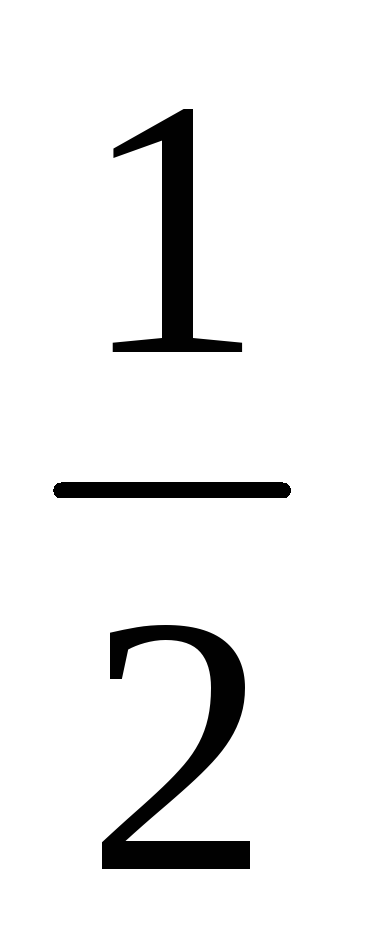 n!
n! -
Подстановка А будет чётной, если общее число инверсий в двух строках любой её записи чётно, и нечётной – в противоположном случае.
-
Произведение любой подстановки А на тождественную подстановку Е, а также произведение Е на А, равно А.
-
Определитель порядка n. Определитель транспонированной матрицы.
Определение.
Определителем
(или детерминантом) матрицы
![]() называется число, которое ставится в
соответствие этой матрице и может быть
вычислено по её элементам по формуле
называется число, которое ставится в
соответствие этой матрице и может быть
вычислено по её элементам по формуле
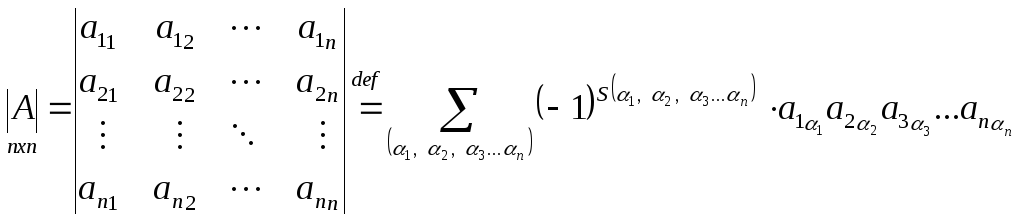
![]() – перестановка
из чисел
– перестановка
из чисел
![]()
![]() –
число инверсий в
перестановке
–
число инверсий в
перестановке
![]()

Определитель транспонированной матрицы.
При транспонировании
матрицы её определитель не меняется,
т. е.
![]() .
Отсюда следует, что любое утверждение,
справедливое для столбцов, будет
справедливо и для строк определителя
матрицы.
.
Отсюда следует, что любое утверждение,
справедливое для столбцов, будет
справедливо и для строк определителя
матрицы.
Доказательство.
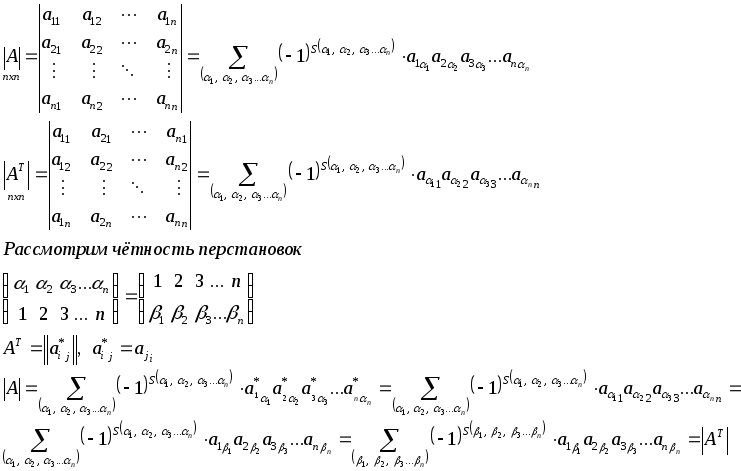
-
Свойства определителя.
-
Свойства определителя:
-
При перестановке двух строк матрицы её определитель меняет знак на противоположный;
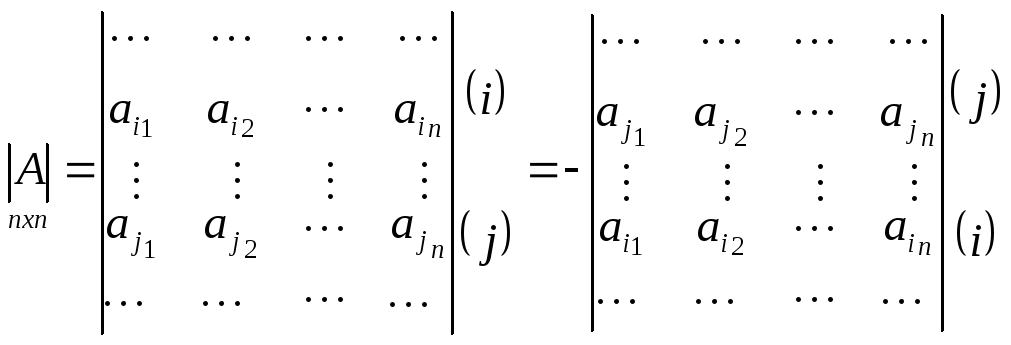
Доказательство.
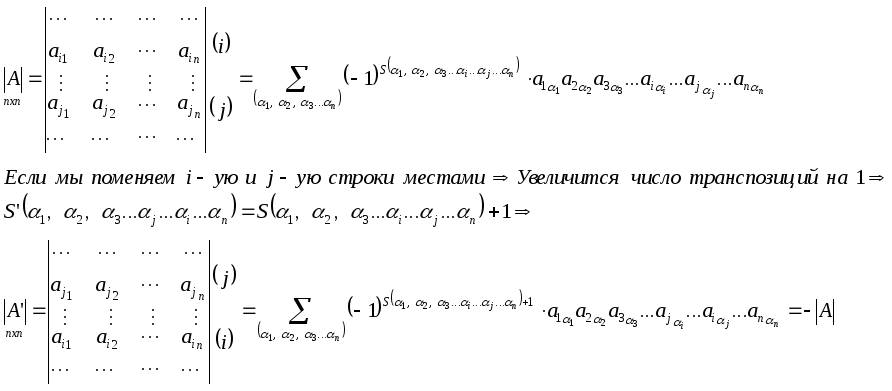
-
Если все элементы какой-либо строки матрицы умножить на какое-то число, то её определить умножится на это число;
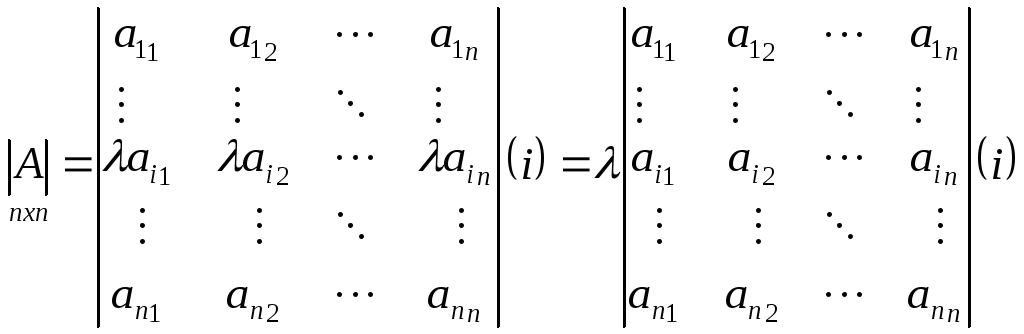
Доказательство.
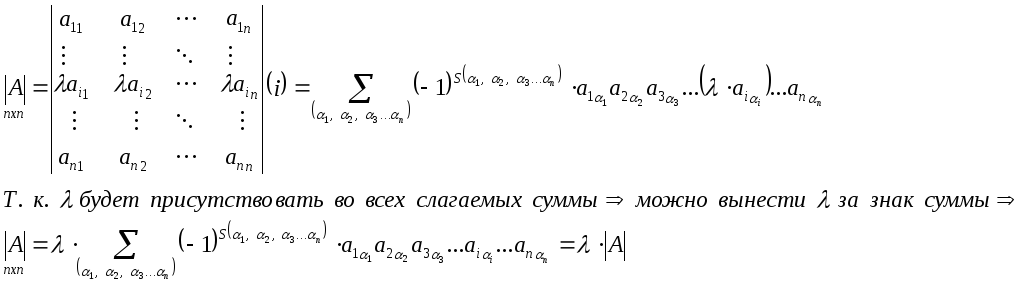
-
Если какая-либо строка матрицы представляет собой сумму двух строк, то определитель этой матрицы можно представить в виде суммы двух определителей.
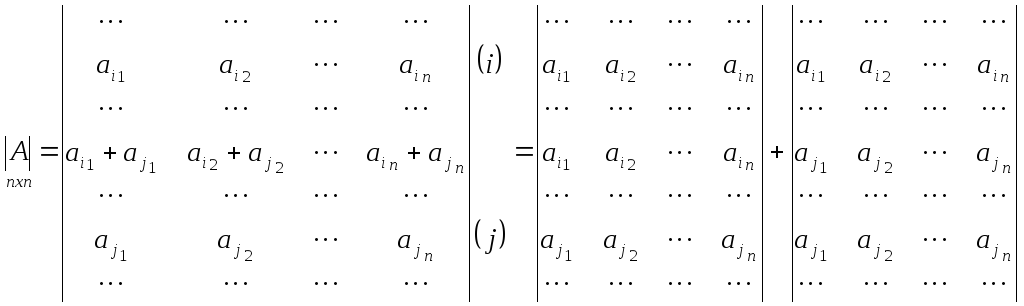
Доказательство.

-
Если матрица имеет две одинаковые строки или содержит строку, состоящую из нулей или соответствующие элементы двух её строк пропорциональны, то определитель матрицы равен нулю.

-
Если к одной строке прибавить соответственно другую строку, умноженную на некоторое число, то определитель не изменится.

-
Миноры. Теорема о произведении минора на его алгебраическое дополнение.
Определение.
Минором матрицы
k-ого
порядка называется определитель матрицы,
состоящей из элементов, расположенных
на пересечении k
строк и k
столбцов (![]() )
данного определителя d
порядка n.
)
данного определителя d
порядка n.
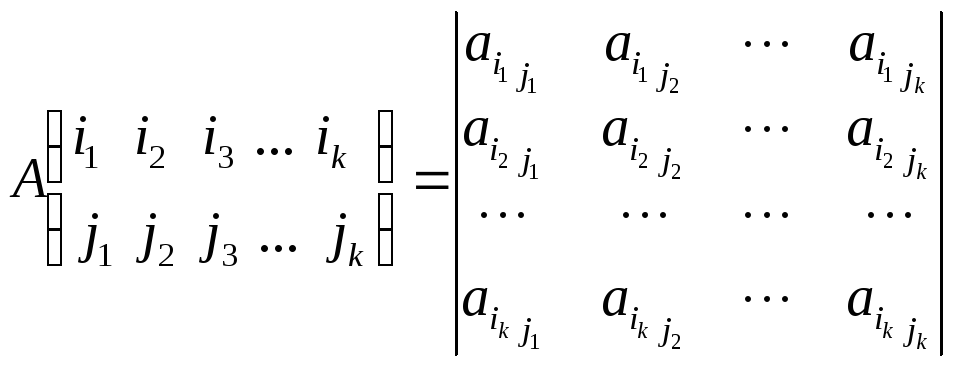
Пусть в определителе d n-ого порядка взят минор M k-ого порядка. Если вычеркнуть те строки и столбцы, на пересечении которых стоит этот минор, то останется минор M’ (n–k)-ого порядка, который называется дополнительным минором для минора М.
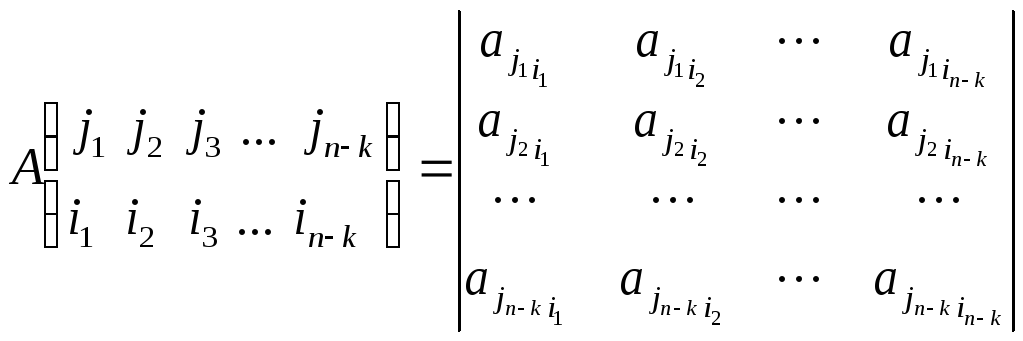
Если минор k-ого
порядка расположен в строках с номерами
![]() и столбцах с номерами
и столбцах с номерами
![]() ,
то алгебраическим дополнением минора
М является дополнительный минор М’,
взятый со знаком
,
то алгебраическим дополнением минора
М является дополнительный минор М’,
взятый со знаком
![]() .
.

Теорема.
Произведением любого минора k-ого порядка матрицы А на его алгебраическое дополнение состоит из слагаемых, представляющих собой члены определителя матрицы А с правильным знаком.
Доказательство.
-
Теорема Лапласа.
Теорема.
Пусть в определителе
d
порядка n
произвольно выбраны k
строк (или k
столбцов),
![]() .
Тогда сумма произведений всех миноров
k-ого
порядка, содержащихся в выбранных
строках, на их алгебраические дополнения
равна определителю d.
.
Тогда сумма произведений всех миноров
k-ого
порядка, содержащихся в выбранных
строках, на их алгебраические дополнения
равна определителю d.
![]()
-
Разложение определителя по строке или столбцу. Умножение элементов строки на алгебраические дополнения к элементам другой строки.
Определение.
Разложение
определителя
 по j-ому
столбцу
по j-ому
столбцу
![]() .
.
Теорема.
Сумма произведений
всех элементов некоторого столбца
(строки) определителя на алгебраические
дополнения соответственных элементов
другого столбца (строки) равна нулю, т.
е.
![]() .
.
-
Правило Крамера.
Пусть дана система, определитель которой не равен нулю, вида
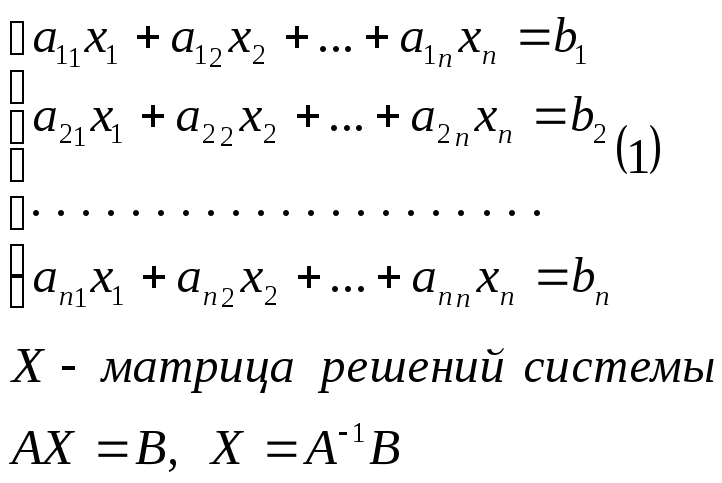
Правило Крамера.
Система (1) однозначно
разрешима при любых правых частях тогда
и только тогда, когда определитель
матрицы А не равен нулю. Это решение
определяется формулой
![]() ,
где
,
где
![]() – определитель матрицы системы,
– определитель матрицы системы,
![]() – определитель матрицы, получаемой из
матрицы системы заменой i-ого
столбца столбцом свободных членов.
– определитель матрицы, получаемой из
матрицы системы заменой i-ого
столбца столбцом свободных членов.
Доказательство.

-
Обратная матрица.
Определение.
Матрица B (A–1) называется обратной к матрице А, если АВ=ВА=Е (единичная матрица).
Теорема.
![]()

-
Ранг матрицы. Теорема о базисном миноре.
Определение.

Определение.
Минор, определяющий ранг матрицы, называется базисным минором. Строки и столбцы, формирующие базисный минор, называются базисными строками и столбцами.
Определение.
Система столбцов
![]() называется линейно зависимой
называется линейно зависимой
![]() ,
не все равные нулю, и такие, что
,
не все равные нулю, и такие, что
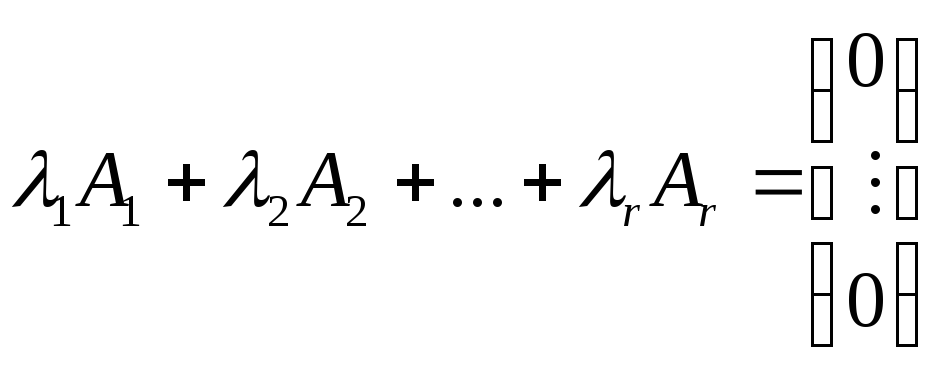
Теорема.
1) Столбцы матрицы А, входящие в базисный минор, образуют линейно-независимую систему.
2) Любой столбец матрицы линейно выражается через столбцы базисного минора.
![]()
Доказательство.


12. 13. Следствия из теоремы о базисном миноре.
Следствия.
а) Равенство определителя нулю.
![]()
Доказательство.

б) Линейная зависимость системы из (n+1) столбца размером из n элементов.

Доказательство.

в) Линейная независимость системы из k столбцов, линейно выражающихся через l столбцов.
![]()
Доказательство.

14. Теорема о ранге матрицы. Критерий линейной зависимости системы столбцов.
Теорема.
Ранг матрицы А равен числу столбцов (строк), входящих в максимальную линейно независимую подсистему.
Доказательство.

15. Метод окаймляющих миноров вычисления ранга матрицы.
Теорема.
Пусть минор k-ого порядка матриц А отличен от нуля, а все окаймляющие его миноры равны нулю, тогда ранг матрицы А равен k.
Доказательство.

16. Элементарные преобразования, не изменяющие ранга матрицы.
Теорема.
Элементарные преобразования, не изменяющие ранга матрицы:
1. Умножение любой строки (столбца) на число отличное от нуля.
2. Перестановка любых двух строк (столбцов).
3. Прибавление к одной строке другой, умноженной на число.
4. Вычёркивание или приписывание нулевой строки.
Доказательство.
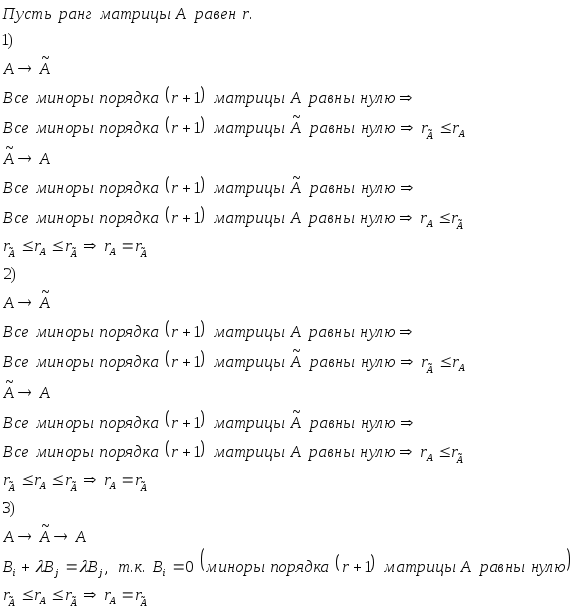
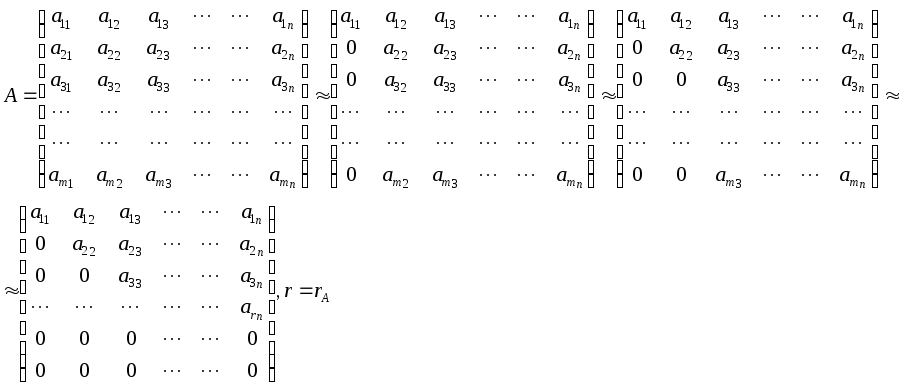
17. Вычисление ранга матрицы методом Гаусса.
Суть метода Гаусса заключается в привидении матрицы А к трапециевидной матрице путём зануления столбцов.
18. Теорема Кронекера-Капелли.
Теорема.

Доказательство.

23. Однородные системы линейных алгебраических дополнений: свойства решений, эквивалентное уравнение системы.

Определение.
Урезанная система – система, из которой отброшены уравнения, у которой соответствующие им строки матрицы системы не входят в базисный минор.
Утверждение.
Урезанная система эквивалентна исходной системе, т. е. любые решения исходной системы равны решениям урезанной системы, и наоборот.
Пример:
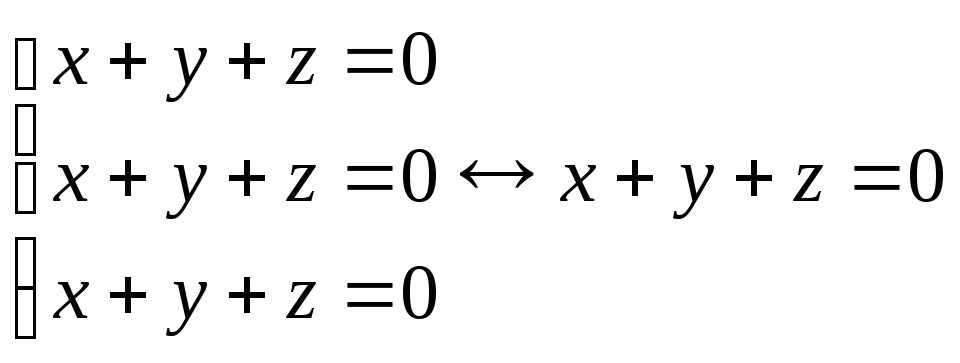
Доказательство.
