Вариант 2

1. Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями α и β. Найдите АВ, если CD = 3 см.

2. Из точки О, лежащей вне двух параллельных плоскостях α и β, проведены три луча, пересекающие плоскости α и β соответственно в точках А, В, С и А₁, В₁, С₁ (ОА < OA₁). Найдите А₁В₁ и В₁С₁, если ОА = 2, АА₁ = 3, АВ = 4, ВС = 5.

3. Постройте сечение, проходящее через точки, выделенные на рисунке.

Контрольная работа № 9

Площадь многогранников

Вариант 1. Вариант 2.

Контрольная работа № 10

Цилиндр, конус и шар

Вариант 1

1) Осевое сечение цилиндра – квадрат. Площадь основания цилиндра равна . Найдите площадь полной поверхности цилиндра.

2) Высота конуса равна 6см. Угол при вершине осевого сечения равен .

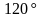а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен .

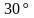б) Найти площадь боковой поверхности конуса.

3) Диаметр шара равен 2рi. Через конец диаметра проведена плоскость под углом 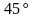к нему. Найдите длину линии пересечения сферы этой плоскостью.

Вариант 2

1) Осевое сечение цилиндра – квадрат, диагональ которого равна 4см. Найдите площадь полной поверхности цилиндра.

2) Радиус основания конуса равен 6см, а образующая наклонена к плоскости основания под углом .

а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен .

б) Найти площадь боковой поверхности конуса.

3) Диаметр шара равен 4pi. Через конец диаметра проведена плоскость под углом к нему. Найдите площадь сечения шара этой плоскостью.

Контрольная работа № 11

Объем прямоугольного параллелепипеда, призмы и пирамиды

Вариант 1

1. Основание прямого параллелепипеда ABCDA₁B₁C₁D₁ ромб с периметром 40 см. Диагональ BD=12 см. Найдите объем параллелепипеда, если его диагональ B₁D=20 см.

2. Боковое ребро правильной треугольной пирамиды равна 6 см, и составляет с плоскостью основания угол . Найдите объем пирамиды.

3. Основанием прямой призмы служит равнобедренный прямоугольный треугольник. Диагональ большей боковой грани равна 8 и составляет с плоскостью основания угол 45º. Найдите объем призмы.

Вариант 2

1. Основание прямого параллелепипеда ABCDA₁B₁C₁D₁ ромб с периметром 20 см. Диагональ BD=6 см. Найдите объем параллелепипеда, если его диагональ B₁D=10 см.

2. Боковое ребро правильной треугольной пирамиды равна 12 см, и составляет с плоскостью основания угол . Найдите объем пирамиды.

3. Основанием прямой призмы служит равнобедренный прямоугольный треугольник. Диагональ большей боковой грани равна 16 и составляет с плоскостью основания угол 45º. Найдите объем призмы.

Контрольная работа № 12

Тела вращения

Вариант 1

1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь боковой поверхности цилиндра.

2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 60. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 45 и площадь боковой поверхности конуса.

3. Диаметр шара равен d. Через конец диаметра проведена плоскость под углом 45 к нему. Найдите площадь сечения шара этой плоскостью.

4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 90. Диагональ сечения равна 10 см и удалена от оси на 4 см. Найдите площадь боковой поверхности цилиндра.