1

ЛАБОРАТОРНАЯ РАБОТА №3

ОБРАБОТКА КОСВЕННЫХ ИЗМЕРЕНИЙ И МАТЕМАТИЧЕСКИЕ ВЫЧИСЛЕНИЯ С РЕЗУЛЬТАТАМИ ИЗМЕРЕНИЙ

1. Цели и задачи работы

Цель: Освоить обработку косвенных вычислений и приближенных значений физических величин.

Задачи:

1. Изучить инженерные методы определения погрешности косвенных измерений.

2. Изучить метод оценки корреляции случайных величин.

3. Освоить методы оценки точности результатов вычислений с использованием приближенных значений.

2. Теоретические положения

1. Косвенные измерения

При косвенных измерениях искомое значение физической величины A находят на основании результатов измерений аргументов а₁, . . . , а_i, . . . , а_m, связанных с искомой величиной уравнением

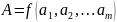_. (1)

Функция f должна быть известна из теоретических предпосылок или установлена экспериментально с погрешностью, которой можно пренебречь.

Результаты измерений аргументов и оценки их погрешностей могут быть получены из прямых, косвенных, совокупных, совместных измерений. Сведения об аргументах могут быть взяты из справочной литературы, технической документации.

При оценивании доверительных границ погрешностей результата косвенного измерения обычно принимают вероятность, равную 0,95 или 0,99. Использование других вероятностей должно быть обосновано.

2. Правила обработки косвенных измерений

Пусть функциональная зависимость между измеряемой величиной A и величинами – аргументами функции. Действительное значение A определяется в соответствии с заданной функцией.

Погрешность косвенного измерения можно оценить различными способами. Ниже приведены три «инженерных» метода, подразумевающих работу с заданными величинами аргументов функциональной зависимости косвенного измерения и их погрешностями.

Метод определения погрешности при помощи частных производных (метод линеаризации)

В данном методе оценивается влияние погрешности каждого аргумента функции на погрешность косвенного измерения по отдельности, с последующим их объединением.

Оценка влияния погрешности аргумента на погрешность функции выполняется по формуле:

(3)

где – погрешность результата от погрешности аргумента , – погрешность аргумента .

Таким образом вычисляются погрешности результата от погрешностей всех аргументов функции: … .

Суть данного метода заключается в следующем: зависимость функции от одного аргумента может быть представлена в виде плоского графика. Геометрический смысл первой частной производная – тангенс угла наклонной касательной. Рассматривая выделенный треугольник на рис. 1 легко понять, что умножив тангенс угла ( ) на длину противоположного катета ( ) образованного прямоугольного треугольника получаем длину прилежащего катета - . Данный метод называется методом линеаризации, т.к. предполагает линейность функции на небольшом отрезке погрешности. Очевидно, что метод будет иметь некоторую погрешность в случае нелинейной зависимости между функцией и аргументом и в ряде случаев не может быть применим.

Итоговое значение погрешности функции рассчитывается по формуле (4) или (5), в зависимости от наличия корреляции между отдельными аргументами функции.

Рис. 1 К оценке погрешности методом линеаризации

Метод определения погрешности при помощи вычисления приращения измеряемой величины по её аргументам

Данный метод также подразумевает необходимость вычисления погрешности результата от погрешностей всех аргументов функции.

Оценка влияния погрешности каждого аргумента на погрешность функции выполняется по формуле:

(4)

Аналогично вычисляются погрешности результата от погрешностей всех аргументов функции: … .

Итоговое значение погрешности функции рассчитывается по формуле (5) или (6).

В зависимости от наличия корреляции между отдельными аргументами функции итоговая величина погрешности косвенного измерения ∆А, вычисляется либо с помощью квадратичного суммирования (5) либо суммирования по модулю её составляющих, вносимых каждым аргументом (6):

(5)

(6)

Квадратичное суммирование применяется в том случае, когда выполняются два условия. Во-первых, погрешность аргументов обусловлена влиянием многих факторов, среди которых нет преобладающего фактора. Во-вторых, погрешности аргументов статистически не связаны т.е. не коррелируют друг с другом. В остальных случаях используется суммирование модулей. Однако правило суммирования часто приводит к завышенному значению погрешности косвенных измерений. Основы определение корреляции между величинами изложены в п. 1.3.

Пример. Пусть значение сопротивления на участке цепи постоянного тока определяется по результатам прямых измерений тока и напряжения на этом участке. Если погрешность измерения тока и напряжения обусловлены влиянием многих факторов (температуры, внутренних сопротивлений амперметра и вольтметра, электрических наводок, нестабильности источника питания и др.),то при суммировании погрешностей лучше использовать формулу квадратичного суммирования. Если погрешность прямых измерений обусловлена в основном случайным изменением внутреннего сопротивлением источника питания, то лучше применить формулу суммирования модулей.

Определение погрешности при помощи формул расчета погрешности косвенных измерений для основных математических операций

Существуют формулы расчета погрешности косвенных измерений при отдельных математических операциях, связывающих аргументы функции косвенного измерения.

Разложив функцию на ряд последовательных математических операций можно рассчитать её погрешность используя формулы для некоторых часто встречающихся на практике функциональных связей (табл. 1). Необходимо учитывать, что результаты, полученные по этим формулам, будут соответствовать модульному суммированию, т.е. в большинстве случаев завышены.

Таблица 1

Формулы погрешностей косвенных измерений

Функциональная связь	Абсолютная погрешность	Относительная погрешность

Погрешность косвенных измерений функции, как правило, больше погрешности прямых измерений её аргументов. Однако в некоторых частных случаях это правило может нарушаться. Рассмотрим такой частный случай на примере измерения периода колебаний

Пример: Пусть при прямом измерении периода колебаний с помощью секундомера получено значение Т=2,0±0,2 с. Тем же секундомером период можно измерить косвенно, зафиксировав время t=200±0.2 с. за которое совершилось N=100 колебаний. Тогда период T=t/N, т.е. Т=2.000±0,002 с. Говорить о том, что в данном случае полная погрешность измерения меньше инструментальной погрешности некорректно, так как речь идет об измерении разных величин, а именно: прямом измерении времени и косвенном измерении периода. Последний вид измерений непосредственно не связан с инструментальной погрешностью.