- •Методическое пособие
- •Приложения производной
- •Содержание
- •Введение
- •Физический и механический смысл производной. Понятие второй производной
- •1. Физический смысл первой производной
- •2. Производная второго порядка. Производная n-го порядка.
- •3. Механический смысл второй производной.
- •Вопросы для самопроверки
- •Приложение производной к решению прикладных задач
- •Понятие касательной и нормали. Геометрический смысл производной
- •1. Понятие касательной и нормали к кривой
- •2. Геометрический смысл производной
- •Решение задач
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Исследование функции на монотонность с помощью производной
- •Признаки возрастания и убывания функции.
- •Вопросы для самопроверки
- •Упражнения
- •Исследование функции на экстремум по первой и второй производной
- •Определение точек экстремума.
- •2. Признаки существования точек экстремума.
- •Второе правило исследования функции на экстремум.
- •Если то - точка максимума,
- •Вопросы для самопроверки
- •Упражнения
- •Задания для самостоятельного решения
- •Применение производной к исследованию функции на монотонность и экстремумы
- •Построение графика квадратного трёхчлена
- •Упражнения
- •Наибольшее и наименьшее значения функции на отрезке
- •1. Найти критические точки, принадлежащие отрезку и вычислить значения функции в этих точках.
- •2. Вычислить значения функции на концах отрезка , то есть найти и .
- •3. Из полученных значений функции выбрать наибольшее и наименьшее.
- •Упражнения
- •Задания для самостоятельного решения
- •Примерный вариант контрольной работы по теме
- •Литература
Вопросы для самопроверки
Сформулируйте признак (прямой и обратный) возрастания функции.
Сформулируйте признак (прямой и обратный) убывания функции.
Как связаны монотонность функции и угол наклона касательной к графику этой функции?
Какие точки называются критическими для функции?
Сформулируйте правило исследования функции на монотонность.
Упражнения
Исследовать функции на монотонность:
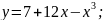 2.
2.
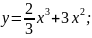
3.
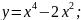 4.
4.
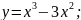
5.
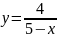 ;
6.
;
6.
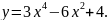
Исследование функции на экстремум по первой и второй производной
Определение точек экстремума.
Рассмотрим график функции , изображённый на рисунке.

Рис.7
В
точках
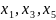 функция переходит от возрастания к
убыванию и в этих точках функция
функция переходит от возрастания к
убыванию и в этих точках функция
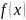 принимает наибольшие значения по
сравнению с рядом лежащими точками.
принимает наибольшие значения по
сравнению с рядом лежащими точками.
В
точках
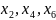 функция переходит от убывания к
возрастанию и в этих точках функция
принимает наименьшие значения по
сравнению с рядом лежащими точками.
функция переходит от убывания к
возрастанию и в этих точках функция
принимает наименьшие значения по
сравнению с рядом лежащими точками.
Вот такие точки функции и называются точками максимума и минимума.
Определение
1. Точка
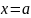 называется точкой
максимума
функции
,
если для всех
называется точкой
максимума
функции
,
если для всех
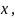 взятых из некоторой окрестности точки
,
выполняется условие
взятых из некоторой окрестности точки
,
выполняется условие
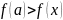
Определение
2. Точка
называется точкой
минимума
функции
,
если для всех
взятых из некоторой окрестности точки
,
выполняется условие
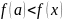
Значения функции в точках максимума и минимума называются соответственно максимумом и минимумом функции.
Максимум и минимум функции объединяют названием экстремумы функции. Точки максимума и минимума называются точками экстремума (или экстремальными точками).


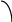
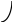
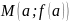

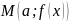


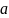 Рис.8
Рис.8
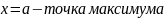
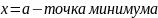
 функции
функции
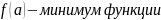
Надо отметить, что максимум функции не всегда является наибольшим значением во всей области определения функции, он является наибольшим лишь по сравнению со значениями функции, взятыми в некоторой окрестности этой точки.
2. Признаки существования точек экстремума.
В точках экстремума функция должна переходить от возрастания к убыванию или от убывания к возрастанию. А это значит, что производная при переходе через эту точку должна поменять свой знак. Это возможно только при переходе производной через ноль или через точку, в которой производная не существует.
Вывод:
если
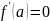 или
или
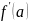 не существует, то функция в точке
может
иметь экстремум.
не существует, то функция в точке
может
иметь экстремум.
Это
условие, являясь необходимым, не является
достаточным. Например, для функции
точка
 не является точкой экстремума, хотя
производная
не является точкой экстремума, хотя
производная
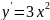 в этой точке
в этой точке
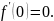
Почему? Потому что производная при переходе через эту точку должна поменять свой знак, а у нас функция остаётся возрастающей и производная знак не меняет.
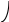
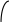
Рис. 9
Итак, получаем теорему, в которой сформулированы необходимое и достаточное условия существования точек экстремума.
Теорема 5. Чтобы точка , была точкой экстремума функции , необходимо и достаточно, чтобы
а) или не существовала,
б) при переходе через точку производная должна менять свой знак.
Эта теорема даёт правило нахождения точек экстремума.
3. Правило исследования функции на экстремум.
Найти производную функции
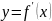 .
.
2. Найти критические точки функции, т.е. значения аргумента , при которых производная или не существует.
3. Определить знак производной , в окрестности критических точек
а) Если при переходе через точку меняет знак с «+» на « - », то - точка максимума;
б) если меняет знак с « - » на «+», то - точка минимума;
в) если знак не меняет, то точкой экстремума не является.
4.
Вычислить значения функции в точках
экстремума
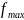 и
и
 .
.
5. При необходимости построить схематически график.
П р и м е р. Исследовать функцию на экстремум и построить схематически график.
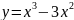
Решение.
1. Найдём производную функции:
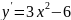 .
.
2. Найдём критические точки:
,
если
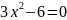 или
или
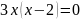 .
.
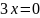 или
или
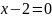
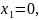
Отметим полученные значения на числовой прямой и определим знак производной в каждом из полученных интервалов.
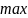
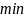

 +
- +
+
- +
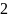
Вычислим значения функции в точках экстремума.
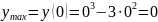 .
Получаем точку
.
.
Получаем точку
.
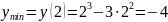 .
Получили точку
.
Получили точку
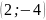 .
.
По полученным точкам строим график.