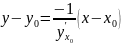- •Методическое пособие
- •Приложения производной
- •Содержание
- •Введение
- •Физический и механический смысл производной. Понятие второй производной
- •1. Физический смысл первой производной
- •2. Производная второго порядка. Производная n-го порядка.
- •3. Механический смысл второй производной.
- •Вопросы для самопроверки
- •Приложение производной к решению прикладных задач
- •Понятие касательной и нормали. Геометрический смысл производной
- •1. Понятие касательной и нормали к кривой
- •2. Геометрический смысл производной
- •Решение задач
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Исследование функции на монотонность с помощью производной
- •Признаки возрастания и убывания функции.
- •Вопросы для самопроверки
- •Упражнения
- •Исследование функции на экстремум по первой и второй производной
- •Определение точек экстремума.
- •2. Признаки существования точек экстремума.
- •Второе правило исследования функции на экстремум.
- •Если то - точка максимума,
- •Вопросы для самопроверки
- •Упражнения
- •Задания для самостоятельного решения
- •Применение производной к исследованию функции на монотонность и экстремумы
- •Построение графика квадратного трёхчлена
- •Упражнения
- •Наибольшее и наименьшее значения функции на отрезке
- •1. Найти критические точки, принадлежащие отрезку и вычислить значения функции в этих точках.
- •2. Вычислить значения функции на концах отрезка , то есть найти и .
- •3. Из полученных значений функции выбрать наибольшее и наименьшее.
- •Упражнения
- •Задания для самостоятельного решения
- •Примерный вариант контрольной работы по теме
- •Литература
Понятие касательной и нормали. Геометрический смысл производной
1. Понятие касательной и нормали к кривой
Мы знаем аналитический и физический смысл производной:
аналитический
смысл – это
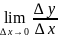 , физический – это скорость процесса,
заданного функцией. Выясним геометрический
смысл производной.
, физический – это скорость процесса,
заданного функцией. Выясним геометрический
смысл производной.
Для этого введём понятие касательной к кривой в данной точке.
Из школьного курса геометрии, вы знаете понятие касательной к окружности. Касательная к окружности определяется как прямая, лежащая в одной плоскости с окружностью и имеющая с ней единственную общую точку.
 Но
такое определение касательной неприменимо
для случая произвольной кривой.
Например, для параболы
Но
такое определение касательной неприменимо
для случая произвольной кривой.
Например, для параболы
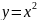 оси
оси
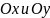 имеют по одной общей точке с параболой.
Однако ось
имеют по одной общей точке с параболой.
Однако ось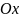 является касательной к параболе, а ось
является касательной к параболе, а ось
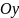 – нет.
– нет.
M1 Дадим общее определение касательной к
L M2 кривой в данной точке.
М3
Пусть
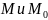 –
некоторые точки произвольной
кривой
–
некоторые точки произвольной
кривой
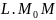 – секущая кривой.
– секущая кривой.
K
При приближении точки
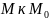 по кривой секущая
по кривой секущая
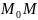 будет поворачиваться вокруг точки
будет поворачиваться вокруг точки
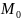 ,
занимая положения
,
занимая положения
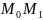 ,
,
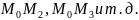
Рис.1
Определение.
Предельное
положение секущей
при неограниченном приближении точки
по кривой называется касательной к
кривой в точке
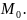
Определение.
Нормалью
к кривой в точке
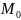 называется прямая, проходящая через
точку
называется прямая, проходящая через
точку
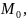 перпендикулярно касательной к кривой
в этой точке.
перпендикулярно касательной к кривой
в этой точке.
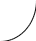
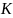 Если
Если
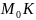 – касательная к кривой
– касательная к кривой
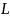 в точке
,
в точке
,
то
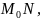 перпендикулярная
будет нормалью к кривой
в точке
перпендикулярная
будет нормалью к кривой
в точке
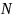
Рис.2
2. Геометрический смысл производной
Пусть
кривая
является графиком функции
.
Точки
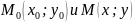
лежат на графике функции. Прямая - секущая кривой . – касательная к кривой

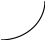

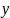

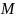
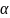 -
угол наклона касательной
-
угол наклона касательной

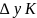
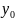
0
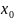
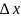
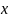 Рис.3
Рис.3
Геометрически,
производная функции
в точке
равна тангенсу угла наклона
касательной, проведённой в точке
или
угловому коэффициенту касательной к
графику функции в этой точке.
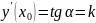
Уравнение
касательной
к кривой
в точке
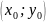 имеет вид
имеет вид
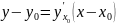
Уравнение нормали к кривой в точке имеет вид