Замечание 2. Функция имеет экстремум только в критических точках. Достаточное условие экстремума.

Пусть функция определена в критической точке x₀ и дифференцируема в некоторой окрестности этой точки, за исключением, может быть, самой x₀. Если «при переходе» через точку x₀ слева направо производная меняет знак с плюса на минус, то x₀ – точка максимума; с минуса на плюс – точка минимума.

Доказательство:

Пусть производная меняет знак с «+» на «-».

Тогда слева от х₀, т.е. на (х₀-δ,х₀) .

Þ слева от х₀ функция возрастает.

Справа от х₀, т.е. на (х_0, х₀+δ) .

Þ справа от х₀ функция убывает.

Т.о. в окрестности точки х₀ выполняется

неравенство .

х₀ – точка локального максимума.

Аналогично доказывается для минимума.

Ч.т.д.

Пример: Исследовать функцию на монотонность и найти точки экстремума.

а) .

1. Область определения функции D(y)=R.

2. .

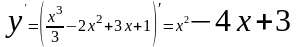Критические точки: 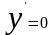. 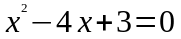Þ , .

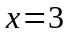x	(-∞;1)	x=1	(1;3)	x=3	(3;+∞)
	+	0	–	0	+
	возрастает	max	убывает	min y(3)=1	возрастает

б) .

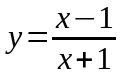1. Область определения функции D(y): x¹-1.

2. ;

.

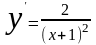Критические точки: , т.е. числитель равен нулю Þ нет точек;

– не существует, т.е. знаменатель равен нулю Þ .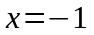

x	(-∞;-1)	x=-1	(-1;+∞)
	+	не существует	+
	возрастает	не существует	возрастает

Точек экстремума нет.

Наибольшее и наименьшее значения функции на отрезке.

Пусть функция определена и непрерывна на замкнутом промежутке [a;b] и имеет внутри этого промежутка конечную производную.

Тогда по второй теореме Вейерштрасса она на этом отрезке принимает свои наибольшее и наименьшее значения.

Очевидно, что эти значения могут достигаться либо в критических точках, либо на концах отрезка.

Поэтому для нахождения наибольшего и наименьшего значений функции применяют следующий алгоритм решения:

1. Находим критические точки функции. Отбираем те точки, которые принадлежат данному отрезку.

2. Вычисляем значения функции в найденных точках.

3. Вычисляем значения функции на концах отрезка.

4. Из полученных значений функции выбираем наибольшее и наименьшее.

Исследование функции на максимум и минимум с помощью производной второго порядка.

Пусть функция определена и непрерывна на промежутке (a;b).

Теорема.

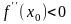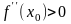Пусть существует и непрерывна в некоторой окрестности точки . Пусть . Если , то в точке функция имеет максимум; если , то в точке функция имеет минимум.

Доказательство:

Докажем для максимума.

Пусть . Пусть .

Так как, по условию, непрерывна в некоторой окрестности точки , то найдется некоторая окрестность , во всех точках которой вторая производная будет отрицательна.

Так как есть производная от первой производной, т.е. 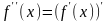, то из условия 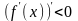следует, что убывает на промежутке, содержащем точку , т.е. в окрестности .

Так как , Тогда слева от , т.е. на (х₀-δ,х₀) имеем , а справа от , т.е. на (х_0, х₀+δ) имеем , т.е. производная «при переходе» через точку x₀ слева направо меняет знак с плюса на минус. А это значит, что точка – точка максимума.

Аналогично доказывается для минимума.

Ч.т.д.

Если в критической точке , то в этой точке может быть или максимум, или минимум или не быть ни максимума, ни минимума. В этом случае исследование проводится с помощью первой производной.

Пример: Исследовать на максимум и минимум функцию.

а) .

1. Область определения функции D(y)=R.

2. .

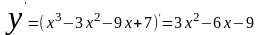Критические точки: . , 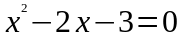Þ , .

3. .

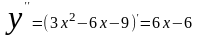x	x=-1	x=3
	-12	12
	max y(-1)=12	min y(3)=-20

б) .

1. Область определения функции D(y)=R.

2. .

Критические точки: . 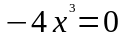Þ .

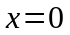3. .

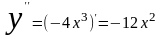x	(-∞;0)	x=0	(0;+∞)
		0
	+	0	–
	возрастает	max y(0)=1	возрастает