Министерство образования и науки российской федерации
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
КУРС ЛЕКЦИЙ
по дисциплине «Математика» 2 семестр
для студентов заочной формы обучения
Раздел №1 «Приложения производной»
Волгодонск
Теоремы о дифференцируемых функциях.
Теорема Ферма.
П
усть
функция
определена и дифференцируема
на
интервале (a;b) и в некоторой точке x0
этого
интервала принимает наибольшее или
наименьшее значение. Тогда
.
Доказательство:
По определению производной:
.
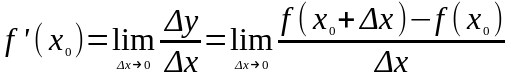Пусть для
определенности в точке
функция
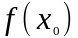принимает
набольшее значение. Тогда числитель
.
Рассмотрим два случая:
1)
.
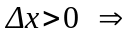
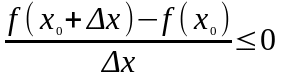По теореме о
предельном переходе в неравенствах:
предел дроби меньше нуля 
.
2)
.
.
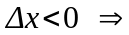
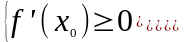
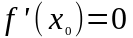Ч.т.д.
Геометрический смысл теоремы Ферма:
Так как
,
то угловой коэффициент касательной
равен нулю
касательная параллельна оси ОХ.
Теорема Ролля.
Пусть функция
определена и непрерывна на отрезке
[a;b] и дифференцируема на интервале
(a;b), причем на концах интервала принимает
одинаковые значения
.
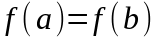Тогда существует точка с(a;b),
значения производной в которой равно
0, т.е.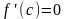
.
Доказательство:
Т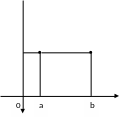
.к.
функция
непрерывна
на отрезке [a;b], то по II-й т. Вейерштрасса
о непрерывных функциях
принимает на [a;b] наибольшее М и наименьшее
m значения. y
Возможны два случая:
1) М=m.
2
)
М
m.
y
Хотя бы одна из точек, в которых функция принимает наибольшее или наименьшее значения, находится внутри [a;b].
В
этом случае в указанной точке выполняются
условия теоремы Ферма и, следовательно,
существует точка c, принадлежащая (a;b),
в которой производная
.
Ч.т.д.
Геометрический смысл теоремы Ролля:
Þ Ккас=0 Þ касательная
в точке c параллельна оси ОX.
Теорема Лагранжа.
Пусть функция
определена и непрерывна на отрезке
[a;b] и дифференцируема на интервале
(a;b). Тогда существует точка c(a;b),
значение производной в которой равно
.
Доказательство:
Введем вспомогательную
функцию
.
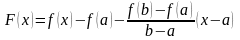Эта функция непрерывна и дифференцируема как сумма непрерывных и дифференцируемых функций.
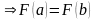
Итак, для F(x) выполняются все условия теоремы Ролля.
существует точка
с(a;b)
такая, что
.
.
Ч.т.д.
Геометрический смысл теоремы Лагранжа:
.
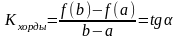
Существует точка cÎ(a;b), в которой угловой коэффициент касательной равен угловому коэффициенту хорды, соединяющей граничные точки:
.
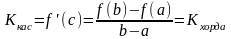Найдется такая точка на графике, касательная в которой параллельна хорде, стягивающей концы отрезка [a;b].
Теорема Коши.
Пусть функции f(x)
и g(x) определены и непрерывны на отрезке
[a;b] и дифференцируемы на интервале
(a;b), причем производная функции g(x)
отлична от нуля, g(x)0.
Тогда существует такая точка c(a;b),
для которой выполняется равенство:
.
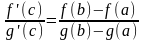Доказательство:
Рассмотрим вспомогательную функцию:
.
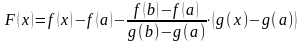непрерывна и
дифференцируема как сумма непрерывных
и дифференцируемых функций.
Итак, для F(x) выполняются все условия
теоремы Ролля.
существует точка с(a;b): .
;
.
.
.
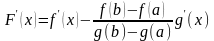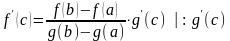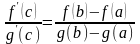Ч.т.д.
Правило Лопиталя.
Теорема.
Пусть функции f(x)
и g(x) определены и дифференцируемы в
некоторой окрестности точки x0,
за исключением может быть самой точки
x0,
и
,
.
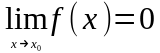Тогда если существует предел отношения
производных функций
,
то существует предел отношения самих
функций
,
причем они равны между собой, т.е.
.
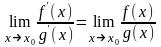Доказательство:
Доопределим f(x) и g(x) в точке x0, положив
f(x0) = g(x0) = 0.
В окрестности точки x0, т.е. на (x0,х) для функций f(x) и g(x) выполняются условия теоремы Коши. Следовательно, существует точка с(x0, х) такая, что
,
т.к. f(x0)
= g(x0)
= 0.
Перейдем к пределу
при x
x0
с
x0:
.
Ч.т.д.
Замечание.
На практике при раскрытии неопределенности
типа
можно пользоваться правилом Лопиталя
и в случаях, когда x,
x.
Для раскрытия
неопределенностей типа
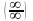существует аналог правила Лопиталя.
Теорема.
Пусть функции f(x)
и g(x) непрерывны и дифференцируемы в
некоторой окрестности точки x0,
за исключением самой точки x0,
причем
.
Пусть
,
.
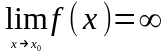Тогда если существует предел отношения
производных функций
,
то существует предел отношения самих
функций
,
причем они равны между собой, т.е.
.
В дальнейшем это утверждение будем также называть правилом Лопиталя.
Замечание 1. Правилом Лопиталя можно пользоваться при раскрытии неопределенностей вида (-), (0), (1), (¥0), (00), сводя их к неопределенностям типа , .
Замечание 2. Если после применения правила Лопиталя опять получаем неопределенность вида или , то его можно применить повторно.
Пример: Вычислить пределы по правилу Лопиталя.
1. Чтобы применять правило Лопиталя при неопределенности вида или , нужно продифференцировать отдельно числитель и знаменатель дроби, и вычислить полученный предел.
.
.
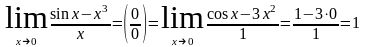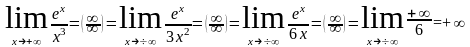Вывод: показательная функция (y=an) всегда растет быстрее, чем степенная (у=xn).
.
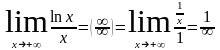Вывод: логарифмическая функция (y=logax) растет медленнее, чем степенная.
2. Неопределенность вида (0) нужно преобразовать в неопределенность вида или , опустив один из множителей в знаменатель в отрицательной степени, и потом применять правило Лопиталя.
3. При показательной неопределенности: (00), (1), (0); прежде чем применять правило Лопиталя, нужно прологарифмировать этот предел по основанию e.
.
=
=
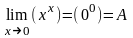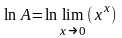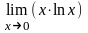=(0×¥)=
=
=
=
=
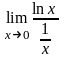=0;
A=e0=1.
Формулы Тейлора и Маклорена.
Пусть функция
n раз дифференцируема в окрестности
точки x0.Найдем
многочлен
степени не выше n-1, такой что
,
,
,…,
.
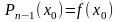Такой многочлен в некотором смысле «близок» к функции .
Будем искать этот
многочлен в форме многочлена, разложенного
по степеням
,
с неопределенными коэффициентами:
.
Неопределенные
коэффициенты
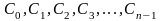определим так, чтобы выполнялись
перечисленные выше условия.
Найдем производные
от
:
;
;…
.
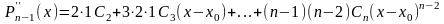Подставляя
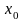вместо
,
находим:
,
,
,
,
… ,
.
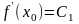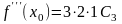Отсюда
Þ
,
,
,
,…,
.
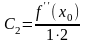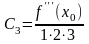Искомый многочлен будет иметь вид:
,
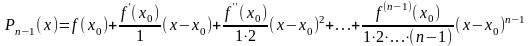или
.
Этот многочлен мы будем называть многочленом Тейлора.
Теорема. Пусть функция n раз дифференцируема в окрестности точки x0. Тогда в этой окрестности для функции справедлива следующая формула Тейлора:
+
+
.
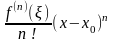Здесь
некоторая точка, заключенная между
и
(
),
зависящая от
,
а
=
-
остаточный член в форме Лагранжа.
Доказательство:
Обозначим через
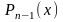многочлен
.
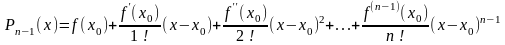Ясно, что для
каждого выбранного
существует такое число
,
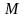для которого будет выполняться равенство:
.
(1)
Покажем, что это
число
при уже выбранном
будет равно
при некотором
из промежутка
.
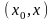Определим функцию
.
Ясно, что
Следовательно,
доказательство мы закончим, если покажем,
что в некоторой точке
(
)
будет выполняться равенство:
.
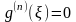Непосредственными
вычислениями проверяется (см. многочлен
Тейлора!), что для всех
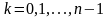выполняются равенства:
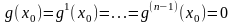(2)
Число
выбрано
таким образом, чтобы выполнялось
равенство (1) и,
следовательно,
.
Таким образом, для функции
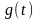на промежутке
[
]
выполняются все условия теоремы Ролля.
Следовательно, на интервале (
)
существует такая точка
,
производная функции
,
в которой равна нулю, то есть
.
Но тогда с учетом (2) теорему Ролля можно
применить к функции
на промежутке [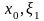
]
и так далее. Применяя, в конце концов,
теорему Ролля к функции
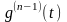на соответствующем промежутке, получим
точку
,
для которой будет справедливо равенство
.
Утверждение доказано.
Если x0=0, то формула Тейлора превращается в формулу Маклорена:
+
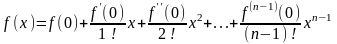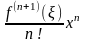
Заметим, что числа n могут выбираться различными, в зависимости и от наличия у функции производных соответствующего порядка, и от необходимой точности расчетов. Например, формула Тейлора для n=4 будет иметь вид:
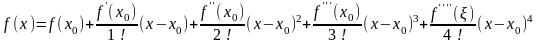
Разложение некоторых элементарных функций по формуле Маклорена.
1.
.
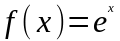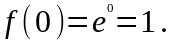
Þ
,
где
.
2.
.
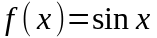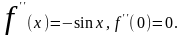
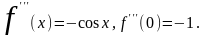
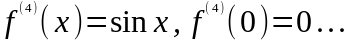
Þ
,
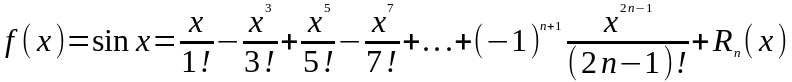где
.
3.
.
,…
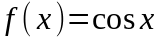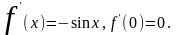
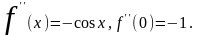
Þ
,
где
.
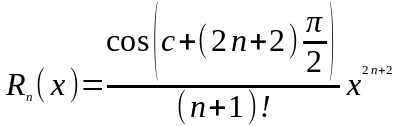Пример:
Разложить функцию
по формуле Маклорена, взяв 4 слагаемых.
Воспользуемся формулой Маклорена для функции , заменив x на
(-x):
.
.
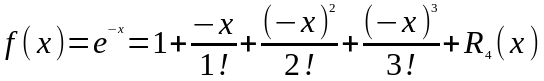