3.3 Матрица линейного оператора при переходе к новому базису.

Если в линейном пространстве действует линейный оператор , то в базисе ему соответствует матрица , а в другом базисе матрица . Эти матрицы линейного оператора связаны между собой следующей формулой:

, (17)

где - матрица перехода от базиса к базису .

Задачи для самостоятельной работы.

1. В пространстве геометрических векторов с базисом , отнесённым к точке 0, заданы линейные операторы , осуществляющий поворот пространства на угол относительно вектора , и , осуществляющий поворот пространства на угол относительно вектора . что этот Составьте матрицы этих операторов. Найдите образы вектора под действием операторов .

Ответ: , , ,

2. В некотором базисе матрица линейного оператора имеет вид . Убедитесь в том, что векторы тоже образуют базис и найдите в этом базисе матрицу данного оператора. Ответ:

Часть 4. Собственные векторы линейного оператора.

4.1 Определение собственного значения и собственного вектора линейного оператора.

Определение. Ненулевой вектор называется собственным вектором линейного оператора , если его образом является вектор, равный произведению вектора на число λ. Число λ называется собственным значением линейного оператора.

Т. е. λ (18)

Если в линейном пространстве, в котором действует оператор , выбран базис, и в этом базисе оператору соответствует матрица А, то из условия следует равенство (19)

Так как матрица А однозначно характеризует действие оператора , то вектор и число λ можно называть собственным вектором и собственным значением матрицы А.

4.2 Нахождение собственных векторов и собственных значений линейного оператора (матрицы а).

Пусть в линейном пространстве L выбран базис, в котором линейный оператор имеет матрицу . Вектор в этом базисе имеет координаты , и ему ставится в соответствие матрица-столбец . Если - собственный вектор линейного оператора, то

Отсюда следует, что или Т. е. (20)

Отсюда следует, что координаты собственного вектора удовлетворяют следующей ОСЛАУ:

(21)

Так как собственный вектор , то ОСЛАУ (21) должна иметь ненулевое решение. Из критерия существования такого решения ОСЛАУ следует, что

. (Или ) Получили уравнение, которое позволит найти собственные значения

(22)

Это уравнение n-ого порядка называется характеристическим .

Из приведённых выкладок следует план нахождения собственных векторов и собственных значений линейного оператора (или матрицы А).

Для заданного линейного оператора , имеющего в некотором базисе матрицу А

1. составляем характеристическое уравнение (22)

и, решая его, находим собственные значения ;

2. для каждого составляем ОСЛАУ (21), которая соответствует равенству , и находим её общее решение, структура которого имеет вид , (23)

где r-ранг матрицы , а - матрицы-столбцы, соответствующие линейно-независимым собственным векторам , найденным для . (24)

Пример 24. Найдём собственные значения и собственные векторы линейного оператора, имеющего в некотором базисе матрицу .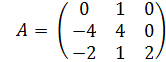

Решение. (см. (22)-(24))

1. Составим характеристическое уравнение и решим его.

Разложим определитель в левой части по элементам последнего столбца.

Найдено единственное собственное значение .

2. Подставляем в ОСЛАУ (21) или (20)

, где - матрица, соответствующая искомому собственному вектору

Очевидно, что в матрице только одна линейно независимая строка и ранг . Откуда следует, что по теореме о структуре общего решения ОСЛАУ

, т. к. (см. (23)).

Т. е. данный оператор имеет два линейно независимых собственных вектора.

Равенство равносильно системе, имеющей только одно уравнение:

, то есть . Тогда

, где , . и - искомые собственные векторы.

Ответ: Любой вектор , полученный при произвольных , не равных нулю одновременно, является собственным вектором оператора с собственным значением , причём два из них, а именно и

линейно независимы между собой.