1.4 Евклидово пространство.

Определение. Линейное пространство называется Евклидовым, если задан закон, по которому каждым двум векторам пространства ставится в соответствие действительное число, называемое скалярным произведением этих векторов

, причём имеют место следующие аксиомы:

1. ;

2. (6)

3. 

4. .

Определение. Нормой вектора называется число . (7)

Определение. Нормированием вектора называется построение вектора такого, что его норма .

Определение. Векторы называются ортогональными, если (8)

Определение. Базис евклидова пространства называется ортонормированным, если его векторы попарно ортогональны и их нормы равны единице, то есть (9)

Замечание. Только в ортонормированном базисе скалярное произведение и вычисляются по формулам , и норма вектора

если , .

Пример 12. Проверим, является ли пространство геометрических векторов с определённым обычным способом скалярным произведением

евклидовым.

Для этого выясним, выполняются ли соответствующие аксиомы. (см.(6))

1. 

2. 

3. 

Эти три аксиомы совпадают со свойствами скалярного произведения.

4. при и 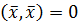, если . – и четвёртая аксиома выполняется.

Вывод: данное пространство является евклидовым.

Пример 13. Выяснить, будет ли являться евклидовым линейное пространство (множество непрерывных на отрезке функций) будет являться евклидовым, если определить скалярное произведение его векторов следующим образом:

Решение. Проверим, выполняются ли соответствующие аксиомы:

1. , так как

, так как

, так как

5. так как (свойство определённого интеграла), причём интеграл обращается в ноль только при .

Ответ: пространство с заданным произведением векторов является евклидовым.

Пример 14. Проверить, можно ли в соответствующем пространстве арифметических векторов задать скалярное произведение следующим образом:

А) , где и - векторы пространства

B) , , где и - векторы пространства .

Решение. А) Проверим, выполняются ли аксиомы для данного произведения.

1. - выполнена;

2. выполнена;

3. - выполнена;

4. - выполнена.

Ответ: так как все аксиомы выполнены, в пространстве таким образом можно задать скалярное произведение.

B) Проверим выполнение аксиом для данного произведения:

1) – выполнена;

2) выполнена;

3) – выполнена;

4) может быть меньше нуля, поэтому аксиома не выполняется.

Ответ: данное произведение векторов не является скалярным.

Замечание. Линейное пространство арифметических векторов

будет являться евклидовым, если скалярное произведение любых двух его векторов в ортонормированном базисе определить следующим образом

Задачи для самостоятельной работы.

1. Проверьте, образует ли линейное пространство множество геометрических векторов, отнесённых к общему началу 0, концы которых принадлежат зафиксированной прямой, не проходящей через точку 0. Ответ: нет.

2. Выясните, является ли линейно зависимой система следующих векторов линейного пространства С: 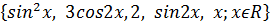. Ответ: да.

3. Выясните, является ли линейно зависимой система следующих векторов линейного пространства : . Ответ: нет.

4. В линейном пространстве многочленов степени не выше третьей выбраны два базиса . Составьте матрицу перехода от первого базиса ко второму и с её помощью разложите многочлен по степеням . Ответ:

5. Убедитесь в том, что в линейном пространстве векторы , , 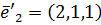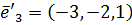образуют базис и найдите координаты вектора в этом базисе. Ответ:

6. Выясните, можно ли в арифметическом пространстве определить скалярное произведение векторов, где и следующим образом: а) . Ответ: можно.

б) . Ответ: нельзя, так как аксиома не выполняется.