20. Линейные оду с переменными коэффициентами. Нахождение общего решения для уравнения 2-го порядка с переменными коэффициентами по одному известному частному решению.

Если известно частное решение 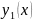ур – ия

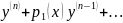
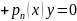, то можно понизить его порядок на единицу, не нарушая линейности ур – ия, полагая , где новая неизвестная ф – ия, сделав затем замену 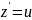или сразу .

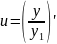Если известно частных л.н.з. решений, то порядок ур – ия можно понизить на единиц.

Для ур – ия 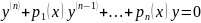общее решение таково:

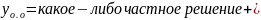общее решение соответствующего однородного ур – ия.

Для нахождения общего решения неоднородного ур - ия при известной фундаментальной системе используется метод Лагранжа (метод вариации постоянных).

Для ур – ия 2 – го порядка:

общий вид ур – ия второго порядка.

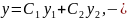вид общего реш –ия соответствующего однородного ур – ия.

вид реш – ия неоднородного ур – ия, 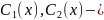некоторые неизвестные ф – ии. Для их определения составляется система:

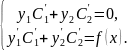
Тогда 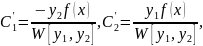где 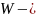определитель Вронского.

21.   Линейные однородные ДУ с постоянными коэффициентами порядка выше 1-ого. Случай действительных корней характеристического многочлена (в том числе и кратных).

Имеем ур – ие , где вещественные постоянные, . Для нахождения общего решения составим характеристическое ур – ие:

.

Вид общего решения зависит от типа корней:

1. , вещественные и различные.

2. , вещественные, но среди них есть кратные ( кратных и ).

22.   Линейные однородные ДУ с постоянными коэффициентами порядка выше 1-ого. Случай комплексных корней характеристического многочлена  (в том числе и кратных).

Имеем ур – ие , где вещественные постоянные, . Для нахождения общего решения составим характеристическое ур – ие:

.

Вид общего решения зависит от типа корней:

1. комплексные, остальные – вещественные.

кратный корень.

23.   Линейные ДУ с постоянными коэффициентами  n-ого порядка. Метод вариации произвольных постоянных.

Линейное ДУ с постоянными коэф – ми 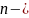ого порядка:

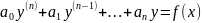, где вещественные постоянные,

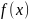, непрерывна на некотором отрезке .

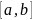Общее решение такого ур – ия имеет вид:

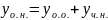
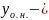решение общее неоднородное

решение общее однородное

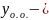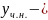решение частное неоднородное

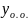составляется с помощью корней соответствующего характеристического ур – ия

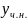зависит от вида правой части ( ).

Метод вариации постоянных

Предположим, что известно и представляется формулой

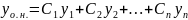
Метод вариации постоянных (или метод Лагранжа) заключается в том, что вместо постоянных чисел мы рассматриваем функции 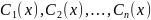. Эти функции подбираются таким образом, чтобы решение 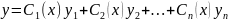удовлетворяло исходному неоднородному уравнению. Производные неизвестных функций определяются из системы уравнений:

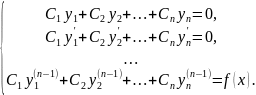
Определителем этой системы является вронскиан функций 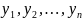, образующих фундаментальную систему решений. В силу линейной независимости этих функций определитель не равен нулю и данная система однозначно разрешима. Окончательные выражения для функций находятся в результате интегрирования.

24.   Линейные ОДУ с постоянными коэффициентами со специальной правой частью. Вид частного решения для всех случаев (таблица для поиска решений).

Линейное ДУ с постоянными коэф – ми ого порядка:

, где вещественные постоянные,

, непрерывна на некотором отрезке .

Общее решение такого ур – ия имеет вид:

зависит от вида правой части ( ).

Если специальная, то решение ищется при помощи таблицы (специальная означает, что ее общий вид представлен в таблице):

25. Метод Лагранжа решения ОДУ n-ого порядка с произвольной непрерывной правой частью.

// Смотреть ответ на вопрос 23, все то же самое.

26.   Система ДУ в канонической форме, их связь с ДУ n-ого порядка (алгоритм приведения).

Система ОДУ

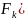
разрешенная относительно старших производных , называется канонической системой. Эта система имеет вид:

Порядком канонической системы называется число 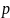, равное:

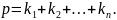
Алгоритм приведения системы ДУ ого порядка к системе канонического вида:

1. Определить порядок системы, т.е. найти 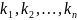и сложить.

2. Выразить ур – ия относительно старших производных от 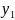до 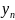и записать в систему.

27.   Система линейных ОДУ 1-ого порядка с постоянными коэффициентами (случай действительных корней)

Система дифференциальных уравнений первого порядка, разрешенных относительно производных называется нормальной системой:

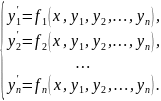
Линейной неоднородной системой дифференциальных уравнений называется система вида

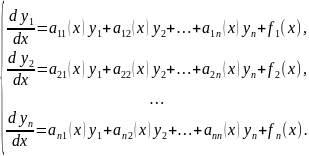
Если 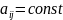, то система с постоянными коэф – ми.

Если все функции 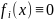, то система дифференциальных уравнений называется линейной однородной системой.

Система в матричном виде:

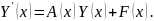
Система в матричном виде может быть решена с помощью метода Эйлера.

По методу Эйлера решение системы ищется в виде 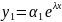, ,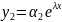…, , 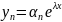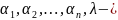постоянные числа, не равны 0 одновременно. Необходимо составить фундаментальную систему, а нулевое решение может не входить в нее.

где

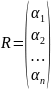
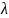находятся из характеристического ур – ия, которое получается из .

Если корни характеристического ур – ия вещественные и различные, то каждому простому действительному корню соответствует вектор 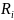и решение системы: , .
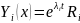
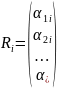