
- •Вопросы по курсу оду 2015-2016 уч. Год.
- •12. Особые решения. Нарушение единственности. Примеры.
- •13. Способы определения особых решений. P и c – дискриминантные кривые.
- •20. Линейные оду с переменными коэффициентами. Нахождение общего решения для уравнения 2-го порядка с переменными коэффициентами по одному известному частному решению.
- •28. Система линейных оду 1-ого порядка с постоянными коэффициентами (случай комплексных корней)
- •29. Общее решение однородной системы линейных оду. Структура общего решения. Метод вариации произвольных постоянных.
Вопросы по курсу оду 2015-2016 уч. Год.
1. Задачи, приводящие к обыкновенным дифференциальным уравнениям (ОДУ).
К понятию обыкновенного дифференциального уравнения приводят физические и геометрические задачи.
Физическая задача. Найти закон движения материальной точки под действием силы тяжести.
Решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения.
Уравнение,
описывающее свободные колебания
материальной точки в среде без
сопротивления является ОДУ и может быть
записано в виде:
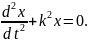
2. Определение ОДУ. Порядок ОДУ. Задача Коши для уравнения n-ого порядка. Общие и частные решения.
Дифференциальным
уравнением называется уравнение,
связывающее независимую переменную
 ,
искомую функцию
,
искомую функцию
 и ее производные
и ее производные
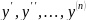 ,
т.е. уравнение вида
,
т.е. уравнение вида
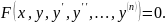
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Задача Коши для любого дифференциального уравнения n -го порядка
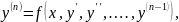
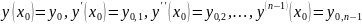 .
.
Общим
решением ДУ
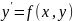 называется ф – ия
называется ф – ия
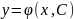 ,
зависящая от одной произвольной
постоянной С.
,
зависящая от одной произвольной
постоянной С.
Частным решением ДУ называется решение, получаемое из общего решения при каком – либо определенном значении С.
3. Геометрический смысл уравнения 1-ого порядка. ОДУ 1-ого порядка, его геометрический смысл. Изоклины.
Общий
вид ДУ 1 – ого порядка:
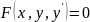 .
=>
.
Уравнение
в каждой точке
.
=>
.
Уравнение
в каждой точке области D,
в которой задана функция
области D,
в которой задана функция
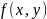 , определяет
, определяет
 -
угловой коэффициент касательной к
решению, проходящему через точку
,
т.е. направление, в котором проходит
решение через эту точку. (Геом. смысл)
-
угловой коэффициент касательной к
решению, проходящему через точку
,
т.е. направление, в котором проходит
решение через эту точку. (Геом. смысл)
Задачи построения интегральной кривой часто решают методом введения изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и то же направление.
4. Теорема Коши существования и единственности решения ОДУ 1-ого порядка, разрешённого относительно производной. ОДУ с разделяющимися переменными.
Пусть
дано ДУ
,
где функция
определена
в некоторой области D
плоскости
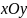 ,
содержащей точку
,
содержащей точку
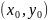 .
Если
удовлетворяет условиям:
.
Если
удовлетворяет условиям:
А)
– непрерывная ф-я 2 – х переменных
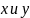 в области D.
в области D.
Б)
имеет частную производную
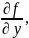 ограниченную в D,
то найдется интервал
ограниченную в D,
то найдется интервал
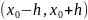 ,
на котором существует единственное
решение
,
на котором существует единственное
решение
 данного уравнения, удовлетворяющее
условию
данного уравнения, удовлетворяющее
условию
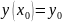 .
.
Уравнение,
в котором коэф – ты при дифференциалах
распадаются на множители, зависящие
только от
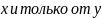 ,
называется ур – ем с разделяющимися
переменными. Общий интеграл такого ур
– ия имеет вид:
,
называется ур – ем с разделяющимися
переменными. Общий интеграл такого ур
– ия имеет вид:

5. Однородные ОДУ 1-ого порядка. Приведение их к уравнениям с разделяющимися переменными.
Функция
 называется однородной ф – ией своих
аргументов измерения n,
если справедливо тождество
называется однородной ф – ией своих
аргументов измерения n,
если справедливо тождество
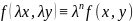 .
.
Путем
замены
 однородное ОДУ 1 – ого порядка приводится
к ур – ию с разделяющимися переменными.
однородное ОДУ 1 – ого порядка приводится
к ур – ию с разделяющимися переменными.
6. Уравнения вида: y’ = f [ (a1x + b1y + c1) / (a2x + b2y +c2) ].
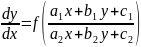 если
если
 ,
то ур – ие однородное и решается с
помощью замены
,
то ур – ие однородное и решается с
помощью замены
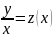 .
Если хоть одно с
отлично от нуля, то ур – ие приводится
к однородному.
.
Если хоть одно с
отлично от нуля, то ур – ие приводится
к однородному.
Если
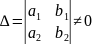 ,
то вводим новые переменные
,
то вводим новые переменные
 ,
,
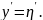
Если
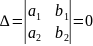 ,
то
,
то
 ,
тогда исходное ур – ие имеет вид:
,
тогда исходное ур – ие имеет вид:
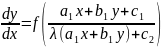 ,
с
помощью подстановки
,
с
помощью подстановки
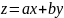 приводим его к ур – ию с разделяющимися
переменными.
приводим его к ур – ию с разделяющимися
переменными.
7. Линейные ОДУ 1-ого порядка. Метод вариации произвольной постоянной. Метод Бернулли.
Линейным ДУ 1 – ого порядка называется ур – ие, линейное относительно неизвестной ф – ии и ее производной.
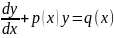
 – общее
решение однородного.
– общее
решение однородного.
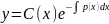 – общее
решение неоднородного, метод вариации
произвольной постоянной. (Варьируется
произвольная константа).
– общее
решение неоднородного, метод вариации
произвольной постоянной. (Варьируется
произвольная константа).
Метод введения двух функций (Бернулли):
Ищем
решение исходного уравнения в виде
произведения двух функций:
y
= u · v,
где u,
v
- функции от x.
Дифференцируем: y′
= u′ · v + u · v′
Подставляем
в исходное уравнение:
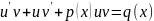 .
.
8. Уравнение
Бернулли. Уравнение в полных
дифференциалах.
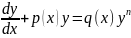
С
помощью замены
 ур – ие Бернулли приводится к линейному
ур – ию и интегрируется как линейное.
ур – ие Бернулли приводится к линейному
ур – ию и интегрируется как линейное.
Ур
– ие Бернулли может быть проинтегрировано
также методом вариации постоянной, как
и линейное ур–ие, и с помощью подстановки
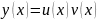 .
.
Ур
– ие
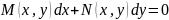 называется ур – ем в полных диф – лах,
если
называется ур – ем в полных диф – лах,
если
 где
где
 некоторая
ф – ия.
некоторая
ф – ия.
9. Интегрирующий множитель. Способы его нахождения.
В
случаях, когда ур – ие
не является ур – ем в полных дифференциалах,
удается подобрать ф – ию
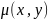 ,
после умножения на которую левая часть
превращается в полный дифф – ал
,
после умножения на которую левая часть
превращается в полный дифф – ал
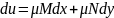 .
.
Такая ф – ия называется интегрирующим множителем.
Частные случаи нахождения интегрирующего множителя.
Если
 ,
то
,
то
 ,
тогда
,
тогда
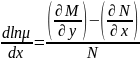 .
Для существования интегрирующего
множителя
правая часть была ф – ей только от
.
Для существования интегрирующего
множителя
правая часть была ф – ей только от

Аналогично, если
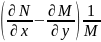 есть ф – ия только от
есть ф – ия только от
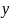 ,
то исходное (первоначальное) ур – ие
имеет интегрирующий множитель
,
то исходное (первоначальное) ур – ие
имеет интегрирующий множитель
 ,
зависящий только от
.
,
зависящий только от
.
10. Уравнения первого порядка не разрешённые относительно производной.
К ур – ям 1 – ого порядка, не разрешенных относительно производной относятся:
Ур – ия первого порядка n-ой степени относительно
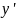 .
.Ур – ия вида

Ур – ия Лагранжа и Клеро.
Пусть имеем ДУ
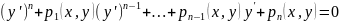
Решаем
его относительно
.
Пусть
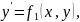
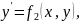 …,
…,
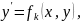
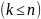 - вещественные решения исходного
уравнения. Тогда общий интеграл исходного
ур – ия выразится совокупностью
интегралов:
- вещественные решения исходного
уравнения. Тогда общий интеграл исходного
ур – ия выразится совокупностью
интегралов:
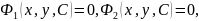 …,
…,
 Т.о.,
через каждую точку области, в которой
Т.о.,
через каждую точку области, в которой
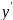 принимает вещественные значения,
проходит
принимает вещественные значения,
проходит
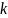 интегральных линий.
интегральных линий.
Случаи, когда ур – ия
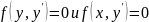 не разрешимы относительно
.
не разрешимы относительно
.
a)
Ур – ие вида
 разрешимо относительно
разрешимо относительно
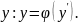 Полагаем
Полагаем
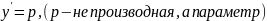 ,
тогда
,
тогда
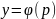 .
Продифференцируем и заменим
.
Продифференцируем и заменим
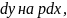 получим
получим
 ,
откуда
,
откуда
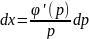 и
и
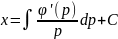 .
Получаем общее решение ур – ия в
параметрической форме:
.
Получаем общее решение ур – ия в
параметрической форме:
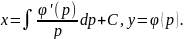
b)
Ур – ие
не разрешимо (или трудно разрешимо) как
относительно
,
так и относительно
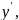 но допускает выражение
и
через некоторый параметр
но допускает выражение
и
через некоторый параметр
 .
.
3)
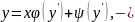 ур – ие Лагранжа.
ур – ие Лагранжа.
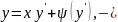 ур
– ие Клеро.
ур
– ие Клеро.
11. Уравнения не содержащие явно искомой функции и уравнения не содержащие явно независимой переменной.
Не содержащие явно искомой функции и ее производных до порядка k – 1 включительно:
Уравнения
вида:
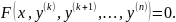
В
уравнениях такого типа возможно понижение
порядка на k
единиц. Для этого производят замену
переменной:
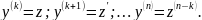
Тогда:
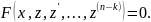
Допустим,
что полученное дифференциальное
уравнение проинтегрировано и совокупность
его решений выражается соотношением:
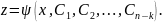
Делая
обратную подстановку, имеем:
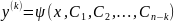 .
.
Интегрируя
полученное соотношение последовательно
k
раз, получаем окончательный ответ:
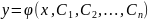 .
.
Не содержащие явно независимой переменной:
Уравнения
вида:
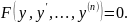
Порядок
таких уравнений может быть понижен на
единицу с помощью замены переменных
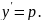
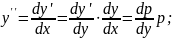
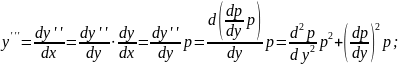 и
т.д.
и
т.д.
Подставляя эти значения в исходное дифференциальное уравнение, получаем:
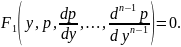
Если
это уравнение проинтегрировать, и
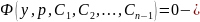 совокупность его решений, то для решения
данного дифференциального уравнения
остается решить уравнение первого
порядка:
совокупность его решений, то для решения
данного дифференциального уравнения
остается решить уравнение первого
порядка:
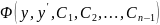 =0.
=0.
