
Задача 4
В результате испытаний центробежного насоса установлено с равной вероятностью, что создаваемый им напор при соответствующих подачах определяется значениями, приведенными в табл.4. Известно также, что напор насоса при его испытаниях измерялся прибором, класс точности и предел измерения которого указаны в таблице.
Установить аналитическую зависимость напора Н от подачи Q.
Таблица 4
Вариант |
Напор насоса Н, м. вод. ст., при подаче Q, м3/ч |
Класс точности и предел измерения прибора, м. вод. ст. |
|||||
10 |
20 |
30 |
40 |
50 |
|
||
7 |
111 |
107 |
90 |
83 |
63 |
3.0 125.0 |
|
Решение
Для выбора вида формулы изобразим табличные данные графически. Наименьшее значение подачи при эксперименте Qнач = 10 м3/ч мало отличается от нуля по сравнению с наибольшим Qкон = 50 м3/ч. Поэтому градуировку шкалы подачи начнем с нулевого значения. Примем длину LQ = 100 мм. Тогда
mQ = LQ/(Qкон - 0) = 100/50 = 2 мм/(м3/ч).
Для напора градуировку шкалы начнем с 50 м вод.ст. Примем длину шкалы LH = 100 мм. В этом случае
mH = LH/(Hкон-Hнач) = 100/(111-63) = 2,083 мм/м вод.ст.
Принимаем mH = 2 мм/м вод.ст. Тогда предельная погрешность в определении напора ΔНпред = 2,5 м вод.ст. на графике будет изображаться отрезком 5 мм.
При mQ = 2 мм/(м3/ч) и mH = 2 мм/м вод.ст. экспериментальная кривая окажется примерно одинаково наклоненной к осям координат. Экспериментальные данные изображены на рисунке 3. Рисунок дает основание предполагать между напором и подачей линейную зависимость. Предположим, что Ĥ = В0 + ВQ.
Рисунок 3. График экспериментальной напорной характеристики центробежного насоса
Для определения коэффициентов уравнения по данным таблицы 4 найдем:
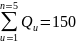 м3/ч;
м3/ч;
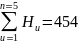 м
вод.ст.;
м
вод.ст.;
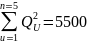 (м3/ч)2;
(м3/ч)2;
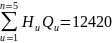 (м
вод.ст.) м3/ч.
(м
вод.ст.) м3/ч.
Найдем В и В0:
454 - 5В0 – 150В = 0;
12420 - 150В0 – 5500В = 0;
Решив данную систему уравнений, получим:
В = -1,2 м вод.ст./( м3/ч);
В0 = 126,8 мм вод.ст.
Таким образом
Ĥ = 126,8 – 1,2Q.
Эта зависимость на рисунке 2 изображена пунктирной линией. Проверим адекватность полученного уравнения регрессии эксперименту. Данные для расчета дисперсии адекватности сведены в таблицу 5.
Таблица 5
HU |
ĤU |
HU - ĤU |
(HU - ĤU)2 |
ĤU1 |
HU - ĤU1 |
(HU - ĤU1)2 |
111 |
114,8 |
-3,8 |
14,44 |
110,8 |
0,2 |
0,04 |
107 |
102,8 |
4,2 |
17,64 |
104,8 |
2,2 |
4,84 |
90 |
90,8 |
0,8 |
0,64 |
94,8 |
-4,8 |
23,04 |
83 |
78,8 |
4,2 |
17,64 |
80,8 |
2,2 |
4,84 |
63 |
66,8 |
-3,8 |
14,44 |
62,8 |
0,2 |
0,04 |
|
|
|
Σ = 64,8 |
|
|
Σ = 32,8 |
Sад2 = 64,8 / (5-2) = 21,6 (м вод.ст.)2.
В соответствии с изложенным, дисперсия воспроизводимости в данном случае:
SВ2 = σ2 = (ΔНпред/2)2 = (2,5/2)2 = 1,5625 (м вод.ст.)2.
Расчетное значение F – критерия:
F = Sад2/ SВ2 = 21,6/1,5625 = 13,824.
Для уровня значимости α = 0,05, а так же чисел степеней свободы fад = 3 и fВ = ∞ табличное значение критерия Fα = 2,6. Так как расчетное значение F – критерия больше табличного, то уравнение не адекватно экспериментальному материалу.
Учитывая, что процессы, протекающие в насосе, дают основание предполагать между напором и подачей квадратичную зависимость, найдем коэффициенты уравнения вида:
ĤU1 = В0' + В'Q2.
По данным эксперимента определим в дополнение к известным:
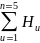 и
и
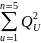 ;
;
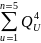 =
9790000 (м3/ч)4
=
9790000 (м3/ч)4
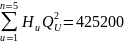 (м
вод.ст.) (м3/ч)2.
(м
вод.ст.) (м3/ч)2.
Полученные величины подставляем в уравнение и составляем систему:
454 - 5В0' – 5500В' = 0;
425200 - 5500В0' – 9790000В' = 0;
Решив данную систему уравнений, получим:
В' = - 0,02 м вод.ст;
В0' = 112,8 м вод.ст./(м3/ч)
Таким образом,
ĤU1 = 112,8 – 0,02Q2.
На рисунке 2 зависимость изображена сплошной линией.
Дисперсия адекватности
Sад2 = 32,8 / (5-2) = 10,9 (м вод.ст.)2.
Расчетное значение критерия Фишера:
F = Sад2/ SВ2 = 10,9/1,5625 = 6,976.
