МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДОНЕЦКОЙ

НАРОДНОЙ РЕСПУБЛИКИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

РЕФЕРАТ

по дисциплине: «Теория инженерного эксперимента»

на тему: «Расчет статистических показателей экспериментальных данных»

Вариант 7

Выполнила:

аспирант кафедры

Геологии и разведки полезных

ископаемых

Лазаренко Е.Н.

Проверил:

Геммерлинг О.А.

Донецк – 2017 г.

План

Задача 1	3
Задача 2	5
Задача 3	8
Задача 4	11
Список литературы	16

Вариант 7 Задача 1

Среднее значение ЭДС самоиндукции e_L для машин постоянного тока является функцией окружной скорости якоря U_a, длины якоря l, линейной нагрузки якоря A и магнитной проводимости µ_α:

e_L= f(U_a, l, A, µ_α) при заданном числе витков в секции ω_с.

Найти безразмерные комбинации, описывающие процесс, если раз­мерности фундаментальных физических переменных имеют вид:

[e_L] = L²МT^-3I^-1; [U_a] = LT^-1; [l] = L; [A] = L^-1I; [µ_α] = LМT^-2I^-2.

Решение

Из условия задачи следует, что размерности всех фундаментальных переменных можно выразить четырьмя основными единицами – М, T, L, I. Так как число m фундаментальных переменных равно 5, а число k основных единиц 4, то независимых критериев будет m – k = 5 – 4 =1. Критерий – безразмерная комбинация – в общем случае может быть представлен произведением фундаментальных переменных в определенных степенях.

Произведение критериев π₁ и π₂ запишем в виде

π₁π₂ = e_L^a U_a^b l^c A^e µ_α^f , (1.1)

где a, b, c, e, f – неизвестные показатели степеней.

Если зависимость 1.1 справедлива относительно переменных, то она будет справедлива и относительно размерностей. Подставим в 1.1 вместо переменных их размерности. При этом будем учитывать, что поскольку критерии безразмерны, то левая часть уравнения представлена произведением размерностей в нулевых степенях:

М⁰T⁰L⁰I⁰ = (L²МT^-3I^-1) ^a (LT^-1) ^b (L) ^c (L^-1I) ^e (LМT^-2I^-2) ^f.

Чтобы последнее выражение было справедливым, должны выполняться условия:

для L

2a + b + c – e + f = 0; (1.2)

для М

a + f = 0; (1.3)

для T

– 3a – b - 2f = 0; (1.4)

для I

– a + e – 2f = 0; (1.5)

В четырех уравнениях пять переменных. Решив совместно уравнения 1.2 – 1.5, можно исключить три переменные. Из выражения 1.3 получаем

f = – a; (1.6)

После подстановки в зависимость 1.4 значения степени f получим

b= – 3a + 2a = – а; (1.7)

Затем подставим в зависимость 1.5 значения степеней f и b в зависимости 1.2 и 1.5:

e = – a; (1.8)

c = – a; (1.9)

Подставим в выражение 1.1 показатели степеней b, c, e, f:

e_L^a U_a^-a l^-a A^-a µ_α^-a = 1, (1.10)

Следовательно

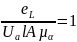(1.11)

Сделаем проверку, подставив размерности вместо переменных в уравнение 1.11:

[(L²МT^-3I^-1)]/[ (LT^-1) (L) (L^-1I) (LМT^-2I^-2)] = 1.

1 = 1

Все размерности сократились, следовательно, уравнение решено правильно.

Задача 2

Определить математическое ожидание, дисперсию, построить полигон, гистограмму, график нормального закона распределения по экспериментальным данным. Число измерений составляет сто.

Решение

1. Экспериментальные данные генерируем в пакете MS Exel. Для этого используем меню «Анализ данных», в нем генерируем массив, указываем количество точек - 100, вид распределения – нормальное. «Анализ данных» устанавливаем через главное меню Exel – настройки – надстройки – Анализ данных – Генерация случайных чисел.

-0,99	25,13	33,71	40,45	49,02	56,74
4,57	25,23	35,99	41,07	49,44	57,40
10,97	25,64	36,01	41,36	49,74	57,96
15,03	25,79	36,04	41,69	50,11	58,17
15,42	25,95	36,08	41,79	50,27	59,78
17,22	25,98	36,41	41,90	50,44	60,23
17,66	26,02	36,44	41,94	50,67	60,96
18,08	26,37	37,05	42,48	51,84	62,13
19,74	27,30	37,05	42,50	52,10	69,48
19,76	27,37	37,24	42,94	52,41	71,86
20,26	27,84	37,57	44,10	52,60
21,41	30,58	38,14	44,63	52,97
21,55	31,98	38,48	45,43	53,49
22,70	32,34	38,72	46,01	53,91
22,76	32,39	39,10	46,04	54,03
23,98	32,51	39,11	46,48	54,90
24,33	32,69	39,44	47,61	55,34
24,77	32,72	40,09	48,91	55,54

2. Весь диапазон значений величин разделяем на равные интервалы. Число интервалов рекомендуется принимать

К = 1 + 3, 32lg n,

где n - число измерений.

Принимаем целое число интервалов равное 8.

3. Затем для каждого интервала определяем количество приходящихся измерений n_U. Отношение этой величины к общему числу измерений n равно вероятности попадания единичных измерений в соответствующий интервал. Относительную частоту попадания или оценку вероятности попадания единичных измерений в соответствующий интервал можно получить, разделив P_u^* на величину интервала (71,86+0,99/К=9,106).

Результаты измерений и вероятностей заносим в таблицу 1.

Таблица 1

Показатель	Диаметр стержня, мм
	-0,99 8,116	8,116 17,222	17,222 26,328	26,328 35,434	35,434 44,54	44,54 53,646	53,646 62,752	62,752 71,86
Число измерений в интервале nU	2	4	19	12	28	20	13	2
Вероятность попадания в интервал, Pu*	0,02	0,04	0,19	0,12	0,28	0,2	0,13	0,02
Оценка вероятности, рu*	0,002	0,004	0,021	0,013	0,031	0,022	0,014	0,002

4. По полученным результатам строим: полигон (рис. 1, а), гистограмму (рис. 1, б) и график нормального закона распределения (закон Гаусса). Для построения закона Гаусса вычисляем параметры нормального закона: m_x и σ (математическое ожидание и среднеквадратическое отклонение) для ста измерений.

а)

б)

Рисунок 1 - Закон распределения вероятностей дискретной случайной величины, представленный в форме полигона (а) и гистограммы (б)

Перед построением графика нормального закона распределения – закона Гаусса (рис. 2) предварительно записываем уравнение и рассчитываем значения в точках, являющихся границами интервалов:

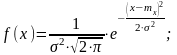
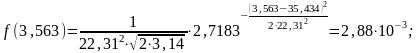
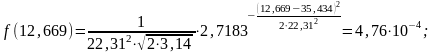
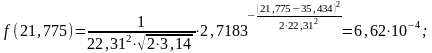
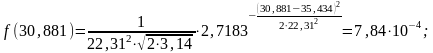
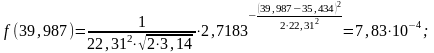
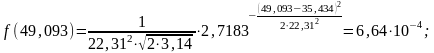
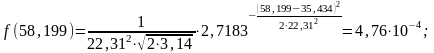
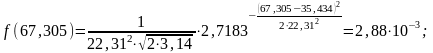
Рисунок 2