§2. Определенный интеграл

2.1. Задача о площади криволинейной трапеции

Рассмотрим криволинейную трапецию ABCD (рис. 2). Найдем площадь этой трапеции. Разделим основание АВ данной фигуры произвольным образом на части и проведем ординаты, соответствующие точкам деления. Тогда криволинейная трапеция разобьется на ряд полосок (см. рис. 2). Заменим теперь приближенно каждую полоску некоторым прямоугольником, основание которого то же, что и у полоски, а высота совпадает с одной из ординат полоски, скажем, крайней слева. Таким образом, криволинейная фигура заменится некоторой ступенчатой фигурой, составленной из отдельных прямоугольников.

Обозначим точки деления:

. (13)

Основание -го прямоугольника , очевидно, равно разности , которая обозначена через . Высота, следовательно, равна , поэтому площадь -го прямоугольника равна .

Просуммировав площади всех прямоугольников, получим приближенное значение площади криволинейной трапеции: .

Погрешность этого равенства при безграничном убывании всех стремится к нулю. Точное значение площади получится как предел

(14)

в предположении, что все одновременно стремятся к нулю. Для предельного значения суммы (14) введено обозначение - в случае площади фиксированной фигуры ABCD, отвечающей изменению от до .

2.2. Понятие определенного интеграла

Пусть определена на отрезке . Разделим отрезок на произвольных частей точками , выберем на каждом элементарном отрезке произвольную точку и найдем длину каждого такого отрезка: .

Определение 2.1. Интегральной суммой для функции на отрезке называется сумма вида (рис. 3):

(15)

Определение 2.2. Определенным интегралом от функции на отрезке (в пределах от до ) называется предел интегральной суммы (15) при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

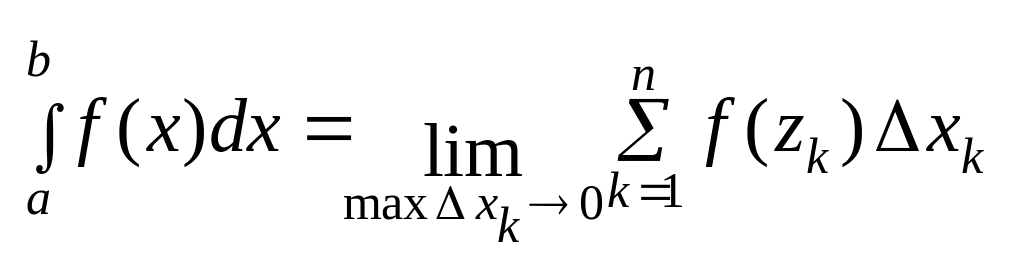. (16)

Если для функции , заданной на отрезке , предел (16) существует и не зависит как от способа разбиения отрезка на элементарные, так и выбора точек , то говорят, что функция интегрируема на отрезке .

Теорема 2.1. (о существовании определенного интеграла)

Если функция непрерывна на отрезке , то она интегрируема на отрезке .

Отметим, что в отличие от неопределенного интеграла, определенный интеграл для фиксированных значений и - число.

2.3. Определенный интеграл как функция верхнего предела

Если функция интегрируема в промежутке , то она интегрируема и в промежутке , где - любое значение из отрезка . Рассмотрим функцию

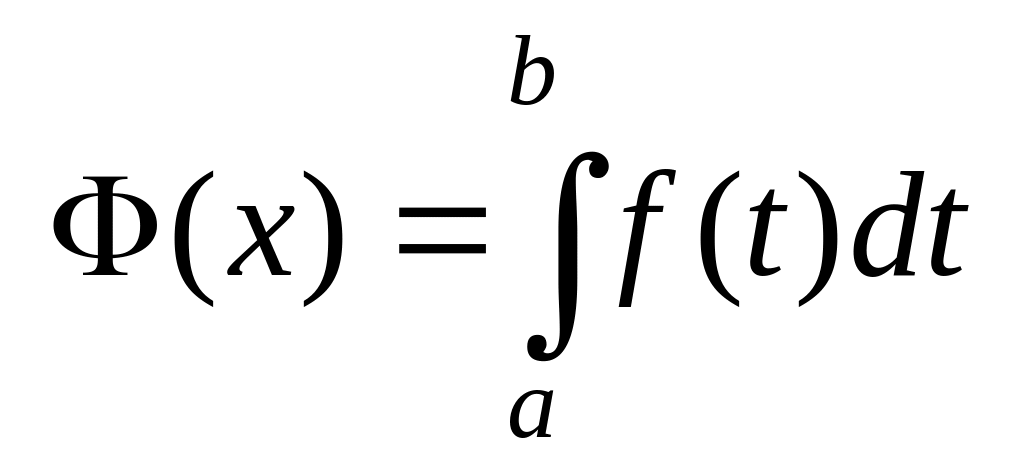(17)

Эта функция обладает следующими свойствами:

1. если функция непрерывна на , то 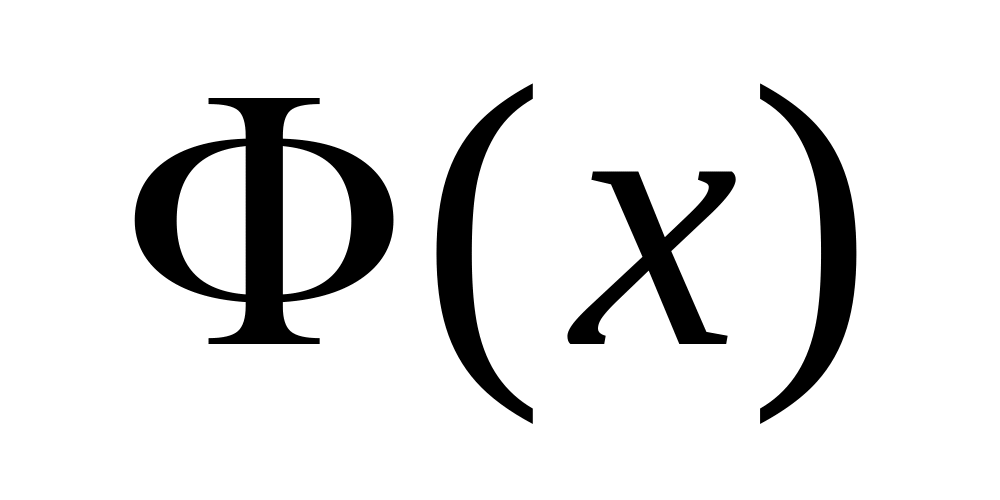будет непрерывной на том же промежутке;

2. если функция непрерывна на , то в любой точке 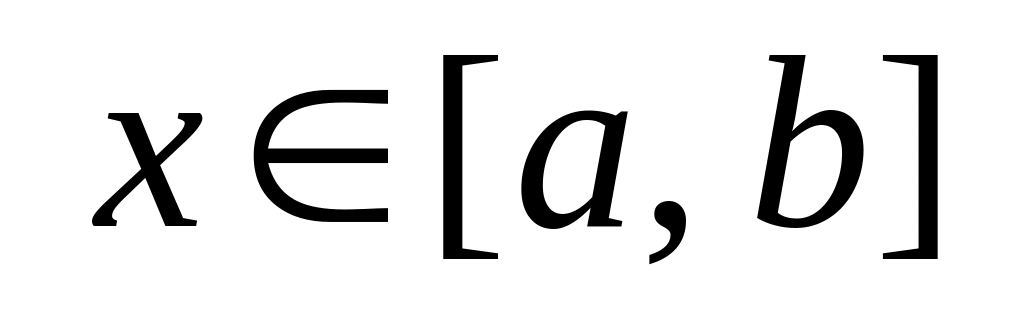функция имеет производную, равную : .

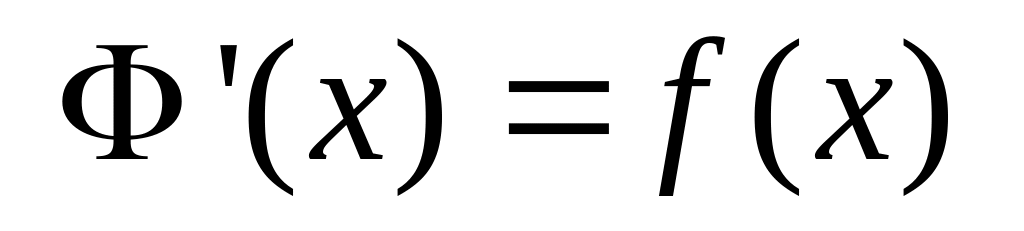Таким образом, функция , определенная равенством (17), является одной из первообразных функции на .